2 Модуль

Занятие № 13. Таблица производных. Непосредственное дифференцирование функций.

Цель занятия: Научить находить табличные производные, применяя к ним правила дифференцирования.

Производной от функциив точкех называется предел отношения её приращения в этой точке к соответствующему приращению аргумента, когда последнее стремится к нулю.

.

Операция нахождения производной называется дифференцированием.

Основные правила дифференцирования

Основные формулы дифференцирования

Применяя формулы и правила дифференцирования, найти производные следующих функций:

Пример 1.

Пример 2.

Пример 3.

Пример 4.

Пример 5.

Пример 6.

Пример 7.

Пример 8.

Занятие № 14. Производная сложной функции. Правила дифференцирования.

Цель занятия: Научить находить производные от сложных функций.

Продифференцировать данные функции:

Пример 1.

Пример 2.

Пример 3.

Пример 4.

Занятие № 15. Производная сложной функции. Производная высших порядков. Производная неявной функции.

Цель занятия: Закрепить нахождение производной от сложной функции и научить находить производные от неявно заданных функций.

Пример 1.

.

В данном примере прежде чем дифференцировать функцию, удобно её прологарифмировать, а затем найти производную как от неявной функции

.

Пример 2.

В данном примере удобно функцию сначала прологарифмировать

Пример 3. Найти и.

arctg y – y + x = 0

Дифференцируем заданное соотношение, рассматривая у как функцию от х:

Находим далее :

В правую часть последнего равенства подставляем вместо его значение

.

Пример 4.

Если функция задана параметрическими уравнениями , то её производная находится по формуле :.

Вторая производная находится по формуле :

;

;

Занятие № 16. Дифференциал функции. Применение дифференциала для приближенных вычислений.

Цель занятия: Научить находить дифференциал первого и высших порядков, а также применять его для приближенных вычислений.

Дифференциалом функции называется главная часть ее приращения, линейная относительно приращения аргумента. Дифференциалом аргумента называется приращение аргумента:.

Дифференциал функции равен произведению ее производной на дифференциал аргумента:

Основные свойства дифференциала:

1. 

2. 

3. 

4. 

5. .

6. 

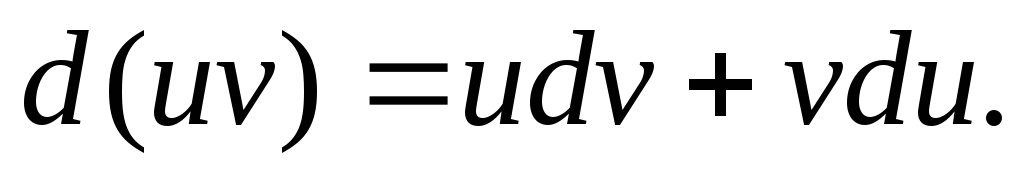
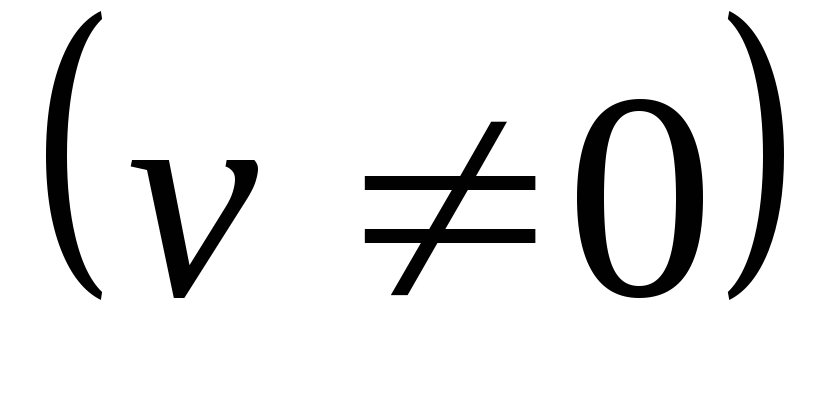Если приращение аргумента мало по абсолютной величине, тои.

Таким образом, дифференциал функции может применятся для приближенных вычислений.

Пример 1. Найти дифференциал функции

Пример 2. Найти дифференциал функции

Пример 3. Найти дифференциалы первого, второго и третьего порядков функции .

Пример 4. Найти дифференциалы первого и второго порядков функции .

Пример 5. Сравнить приращение и дифференциал функции .

Пример 6. Вычислить приближенное значение arcsin 0,51.

Пример 7. Вычислить приближенное значение площади круга, радиус которого равен 3,02 м.

Пример 8. Вычислить приближенное значение объема шара радиуса 2,01 м.

Занятие № 17. Правило Лопиталя.

Цель занятия: Научить вычислять пределы по данному правилу.

Правило Лопиталя. Если функции ибесконечно малые или бесконечно большие при, дифференцируемы в окрестности точки,в окрестности этой точки, существует, то существуети справедливо равенство:.

Эта теорема справедлива и при и позволяет раскрывать неопределённостии. Другие виды неопределённостей приводят к этим двум преобразованием выражения под знаком предела.

Найти указанные пределы, используя правило Лопиталя.

Пример 1.

Здесь неопределённость вида . Применяя правило Лопиталя, имеем

Пример 2.

Здесь для получения результата приходится применять правило Лопиталя дважды, так как и данное отношение и отношение производных приводят к неопределённости типа . Повторные применения правила Лопиталя записываются обычно в одну цепочку равенств.

Пример 3.

Здесь неопределённость вида . Положим. Логарифмируя и применяя правило Лопиталя, получим

Таким образом,

Пример 4.

Это – неопределённость вида . Положими прологарифмируем:

Применяя правило Лопиталя, получим

, т.е.

Занятие № 18. Исследование функций с помощью производной.

Цель занятия: Показать на примерах различные способы исследования для разных функций.

Если в некоторой окрестности точки выполняется неравенствоили, то точканазываетсяточкой экстремума функции (соответственно точкой максимума или минимума).Необходимое условие экстремума: если – экстремальная точка функции, то первая производнаялибо равна нулю или бесконечности, либо не существует.Достаточное условие экстремума: является экстремальной точкой функции, если её первая производнаяменяет знак при переходе через точку: с плюса на минус – при максимуме, с минуса на плюс – при минимуме.

Кривая вогнута вверх (обозначают  ) на интервале , если в каждой точке этого интервала выполнено условиеприивогнута вниз (обозначают  ), если при.

Точка называетсяточкой перегиба кривой , если при переходе через точку меняется направление выпуклости.Необходимое условие точки перегиба: если - точка перегиба кривой, то вторая производнаялибо равна нулю или бесконечности, либо не существует.Достаточное условие точки перегиба: является точкой перегиба кривой, если при переходе через точкувторая производнаяменяет знак.

Прямая являетсянаклонной асимптотой кривой , если расстояние от точки кривой до этой прямой стремится к нулю при. При этом

.

При имеемгоризонтальную асимптоту:

Если то прямаяназываетсявертикальной асимптотой.

Пример 1. Найти наибольшее и наименьшее значения функции на отрезке.

Решение. Наибольшее и наименьшее значения функции на замкнутом интервале достигаются или в точках экстремума, которые являются критическими точками функции, или на концах интервала. Задача сводится к сравнению между собой значений функции в указанных точках.

Находим стационарные точки:

Определяем значение функции в этих точках и на концах интервала

Среди полученных значений выбираем наибольшее и наименьшее

Пример 2. Найти интервалы возрастания и убывания функции .

Пример 3. Исследовать на экстремум функцию .

Пример 4. Исследовать на экстремум функцию .

Пример 5. Найти наибольшее и наименьшее значения функции на отрезке [-2; 3].

Пример 6. Найти интервалы выпуклости и вогнутости кривой .

Пример 7. Найти точки перегиба кривой .

Пример 8. Найти асимптоты кривой .

Занятие № 19. Исследование функции с помощью производной и построение графиков.

Цель занятия: научить проводить полное исследование функции и строить графики.

Общая схема построения графика функции

1. Найти область определения.

2. Исследовать функцию на симметричность.

3. Исследовать функцию на периодичность.

4. Определить точки пересечения графика функции с координатными осями.

5. Найти интервалы монотонности и точки экстремума функции.

6. Найти интервалы выпуклости, вогнутости графика функции и точки перегиба.

7. Выяснить существование асимптот.

8. Построить график функции.

Провести полное исследование указанных функций и построить их графики.

Пример 1.

.