Лабораторна робота № 1 вивчення криволінійного руху.

Мета роботи – визначити деякі кінематичні характеристики (горизонтальну і вертикальну складові швидкості, повну швидкість, нормальну і тангенціальну (дотичну) складові повного прискорення, а також радіус кривизни траєкторії) руху тіла, що кинуте горизонтально в полі тяжіння Землі, в заданій точці траєкторії.

Прилади і обладнання: криволінійний жолоб, стальна кулька, обмежувальний ящик, масштабна лінійка, звичайний та копіювальний папір.

Теоретичні відомості

Якщо матеріальна точка рухається за криволінійною траєкторією, то вектор її лінійної швидкості збігається з дотичною до траєкторії. При цьому вектор швидкості може змінюватись в загальному випадку як за модулем, так і за напрямком.

Вектор тангенціального прискорення визначається швидкістю зміни вектора швидкостіза модулем, вектор нормального (доцентрового) прискорення- швидкістю зміни вектора швидкості за напрямком.

Рисунок 1

Напрямок вектора тангенціального прискорення в кожній точці траєкторії (див. рис.1, точка M) збігається з напрямком вектора повної швидкості, а його модуль визначається першою похідною від швидкості за часом: .

Вектор нормального прискорення спрямований до центра кривизни траєкторії під кутом 90⁰ до вектора повної швидкості. Його модуль , де v – повна швидкість в точці траєкторії M, R – радіус кривизни траєкторії в цій точці. Вектори тангенціального і нормального прискорення є взаємно перпендикулярними складовими повного прискорення, яке дорівнює їх векторній (геометричній) сумі:. Модуль вектора повного прискорення.

При кидані деякого тіла в горизонтальному напрямку (вздовж осі ОХ) його рух обумовлюється рухом за інерцією в горизонтальному напрямку і рухом під дією сили тяжіння – в вертикальному. Згідно принципу незалежного складання рухів ці два рухи дають результуючий рух за криволінійною траєкторією. Його описує рівняння руху в двох координатах:

ОХ: , (1)

ОУ: , (2)

де - початкова швидкість вздовж осі ОХ (початкова швидкість в вертикальному напрямку дорівнює нулю), H – висота, з якій падає кулька, g – прискорення вільного падіння. Ми нехтуємо силою опору повітря і тому вважаємо рух вздовж осі ОХ рівномірним, тобто горизонтальна складова швидкості завжди v_г = v_ox = v_о. Цей рух і рух по вертикалі синхронізовані у часі, але є незалежними. Диференціювання по часу другого рівняння дає вираз для величини вертикальної складової швидкості

v_В = v_y: . (3)

Рівняння (1) - (3) дозволяють з відомих початкових умов визначити кінематичні характеристики руху матеріальної точки в будь-який момент часу (це є пряма задача кінематики), наприклад, для моменту падіння маємо:

; ;

(4)

В даній лабораторній роботі відомими з експерименту є величини H i L, що дозволяє розрахувати інші відповідні кінематичні характеристики.

Опис методу

Для створення горизонтального руху тіла (стальної кульки) застосовується жолоб N, що закріплений на тримачі D (рис.2). Кульку утримують над жолобом на рівні його верхнього краю, а потім відпускають. Нижній кінець жолоба спрямований горизонтально, тому і вектор швидкості кульки в точці вильоту спрямований горизонтально.

Значення горизонтальної складової швидкості є однаковим в кожній точці траєкторії і дорівнює

(5)

значення вертикальної складової дорівнює

. (6)

Для величини повної швидкості в точці падіння, враховуючи вищенаведені формули, маємо

. (7)

Рисунок 2

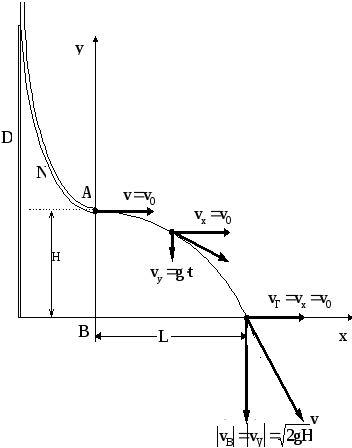
Повне прискорення в будь-якій точці дорівнює прискоренню вільного падіння . Розкладемо його на дві складові – тангенціальну (дотичну)і нормальну (доцентрову).

Знайдемо формули для обчислення цих величин. З рис.3 бачимо, що трикутники ABC і DFC є подібні, тому

маємо , звідки. (8)

Також , звідки. (9)

Знаючи ідля точки С, можна визначити радіус кривизни траєкторії в цій точці:(10)

Рисунок 3

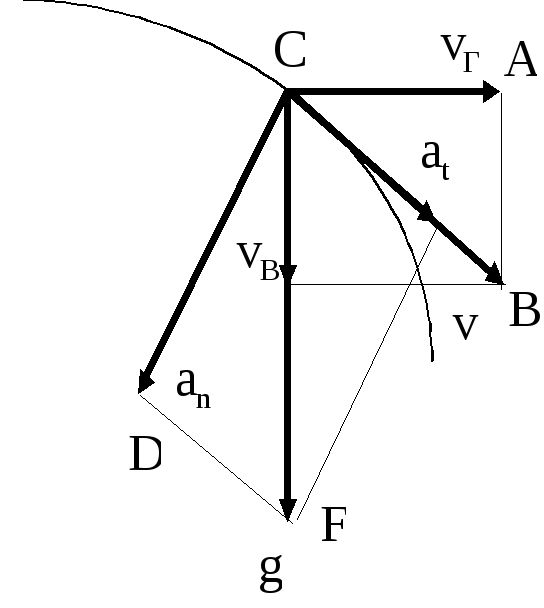
В роботі необхідно визначити величини: v_Г, v_В, v, a_t, a_n, a, R в точці падіння, виходячи з виміряних значень L і H.