2. Определение дифференциальной функции распределения. Доказ-во свойств.

Производная интегральной функции распределения непрерывной CВ Х называется дифференциальной функцией распределения СВ.

Свойства.

1. Функция f(x) определена при всех значениях Х, D(f)=К.

2. Дифферен. функция распределения f(x) – неотрицательная функция. f(x)≥0,

Док-во. Т.к. F(x) – неубывающая функция, то f(x)=F`(x)≥0

3. Вероятность того, что непрерывная CВ примет значения из промежутка (a;b) находится по формуле:

Док-во. Рассмотрим интеграл

F(x) – первообразная для функции f(x) и по формуле Ньютона-Лейбница имеем:

(вероятность достоверного событ. =1).

1. Центральная предельная теорема. Вывести интегральную теорему Муавра-Лапласа. Её частные случаи.

Теорема. Пусть Х₁, Х₂, …, Х_n - независимые СВ. а₁, а₂, … , а_n - соответственно их математ. ожидания, D(X₁), D(X₂), …, D(X_n) – их дисперсии. Если эти CВ сравнимы по порядку своего влияния на рассеивание суммы, а число их достаточно велико, то вероятность попадания их суммы в интервал (x₁;x₂) находится по формуле:

где а=а₁+а₂+…+а_n,

Таким образом, чтобы приближённо найти вероятность попадания суммы большого числа CВ на заданный промежуток, не требуется знать их законы распределения, достаточно знать их числовые хар-ки.

Теорема Муавра-Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число m наступления события А в n независимых повторных испытаниях заключено в пределах от m₁ до m₂ включительно при достаточно больших n приближённо находится по формуле:

гдефункция Лапласа.

Частные случаи. Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе испытаний n справедливо следующие приближённые равенства:

11. Схема применения критерия Пирсона.

1. Выбираем предполагаемый закон распределения и находим его параметры.

2. Вычисляем теоретические частоты по формуле . Вероятностьнаходится по формуле в соответствии с выбранным законом.

3. Находим величину 4. Определяем по формуле, гдечисло интервалов эмпирического распределения,сумма числа параметров предполагаемого теоретического закона и числа дополнительных соотношений эмпирических частот.

5. Выбираем уровень значимости , например.

6. По таблице находим вероятность события .

7. Если , то расхождения между теоретическими частотами и эмпирическими частотами носят случайный характер и следует принять гипотезу о предполагаемом законе распределения, в противном случае гипотезу следует отвергнуть.

13. Точечные оценки выборки и требования к ним.

Пусть необходимо оценить некоторый параметр 0, присущий элементам г.с. Для этого делается выборка объема n и по результатам выборки получается значение 0* . Оценка 0* зависит от объема выборки, а при фиксированном объеме, зависит от элементов, попавших в выборку. Поскольку выбор элементов происходит случайно, то 0* является случайной величиной. 0* называется точечной оценкой параметра 0. Точечная оценка должна быть:

а)Оценка 0* параметра 0 называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е. М(0*) = 0. В противном случае оценка называется смещенной. Требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.

б)Оценка 0* параметра 0 называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:

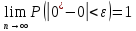
в)Несмещенная оценка 0* параметра 0 называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра 0, вычисленных по выборкам одного и того же объема.

Точечная оценка 0*, является лишь приближенным значением неизвестного параметра 0 даже в том случае, если она несмещенная, состоятельная и эффективная и для выборки малого объема может существенно отличаться от параметра 0. Чтобы получить представление о точности и надежности оценки 0* параметра 0 используют интервальную оценку параметра.