
- •Лабораторная работа № 4 Исследование частотных свойств электрических цепей переменного тока с реактивными lс - элементами.
- •4.1 Исследование фильтров нижних и верхних частот
- •Оборудование и аппаратура
- •Порядок выполнения работы
- •4.2 Исследование резонансного контура
- •Порядок выполнения работы
- •Ответить устно на следующие вопросы
Лабораторная работа № 4 Исследование частотных свойств электрических цепей переменного тока с реактивными lс - элементами.
4.1 Исследование фильтров нижних и верхних частот
Цель работы. Ознакомиться с простейшими цепями переменного тока, состоящие из емкостных и индуктивных элементов, образующие частотные фильтры и резонансные контура; измерить величины токов и напряжений на отдельных участках цепи.
Задание на подготовку к лабораторной работе.
В результате изучения теоретического материала студент должен
знать:
- виды электрических фильтров и их основные характеристики;
- физическую сущность процесса возникновения резонанса в электрических цепях;
- влияние параметров отдельных элементов на величину частоты резонанса и ширину полосы пропускания контура.
Уметь:
- рассчитывать и практически определять полосу пропускания фильтра;
- строить амплитудночастотную характеристику фильтра по точкам с помощью вольтметра или осциллографа;
- рассчитывать и практически определять резонансную частоту и полосу пропускания колебательного контура;
Пояснения. В практике электротехники часто возникает необходимость придать цепи частотноселективные свойства. Т.е. колебания, например нижних частот , должны проходить с минимальными потерями, а колебания верхних частот –с большим ослаблением. Такая цепь называется частотным фильтром нижних частот. Cуществуют и используются также частотные фильтры верхних частот – пропускающие только верхние частоты, , полосовые – пропускающие частоты от и до какой-то величины и режекторные – не пропускающие частоты от и до какой-то величины.
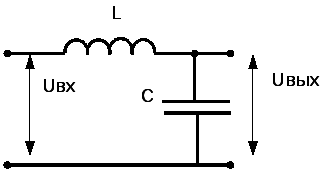
Рис.11 – Звено фильтра нижних частот.
На Рис.11 показан пример простейшего LC-фильтра нижних частот (ФНЧ): при подаче сигнала определённой частоты на вход фильтра (слева), напряжение на выходе фильтра (справа) определяется отношением реактивных сопротивлений катушки индуктивности (XL = ωL) и конденсатора (XC = 1 / ωC).
Коэффициент
передачи ФНЧ можно вычислить, рассматривая
делитель напряжения, образованный
частотно-зависимыми сопротивлениями
реактивностей L
и
С.
Комплексное
(с учетом сдвига фаз между напряжением
и током) сопротивление катушки
индуктивности есть ZL
= jωL
= jXL
и конденсатора ZC
= 1 / (jωC)
= − jXC,
где
![]() и ω = 2πF. Поэтому, дляненагруженного
LC-фильтра
коэффициент передачи будет:
и ω = 2πF. Поэтому, дляненагруженного
LC-фильтра
коэффициент передачи будет:
 .
.
Подставляя значения сопротивлений, получим для частотно-зависимого коэффициента передачи:
![]() .
.
Как
видно, коэффициент передачи ненагруженного
идеального ФНЧ неограниченно растет с
приближением к частоте
![]() ,
и затем убывает. На очень низких частотах
коэффициент передачи ФНЧ близок к
единице, на очень высоких — к нулю.
Зависимость модуля комплексного
коэффицента передачи фильтра от частоты
называютамлитудно-частотной
характеристикой
(АЧХ) , представлена на Рис.12. Для
удобства сравнения по вертикальной оси
откладывается не абсолютное значение
коэффициента передачи, а нормированное
к максимальному, т.е. К 0
= К / К max.
,
и затем убывает. На очень низких частотах
коэффициент передачи ФНЧ близок к
единице, на очень высоких — к нулю.
Зависимость модуля комплексного
коэффицента передачи фильтра от частоты
называютамлитудно-частотной
характеристикой
(АЧХ) , представлена на Рис.12. Для
удобства сравнения по вертикальной оси
откладывается не абсолютное значение
коэффициента передачи, а нормированное
к максимальному, т.е. К 0
= К / К max.
В
реальных схемах к выходу фильтра
подключается активная нагрузка, которая
понижает добротность фильтра и
предотвращает резонанс АЧХ вблизи
частоты ω0.
Величина этого сопротивления определяется
по формуле
![]() и называютхарактеристическим
сопротивлением фильтра.
ФНЧ, нагруженный на сопротивление,
равное характеристическому, имеет
нерезонансную (равномерную) АЧХ, примерно
постоянную для частот ω
< ω0,
и убывающую как 1
/ ω2
на частотах выше ω0.
Поэтому, частоту ω0
называют частотой
среза и она
определяет полосу пропускания фильтра.На практике принято
отсчитывать полосу пропускания при
уменьшении относительного коэффициента
передачи до уровня 0,707.
и называютхарактеристическим
сопротивлением фильтра.
ФНЧ, нагруженный на сопротивление,
равное характеристическому, имеет
нерезонансную (равномерную) АЧХ, примерно
постоянную для частот ω
< ω0,
и убывающую как 1
/ ω2
на частотах выше ω0.
Поэтому, частоту ω0
называют частотой
среза и она
определяет полосу пропускания фильтра.На практике принято
отсчитывать полосу пропускания при
уменьшении относительного коэффициента
передачи до уровня 0,707.

Рис. 12 – Амплитудно-частотная характеристика ФНЧ.
Аналогичным образом строится и LC-фильтр верхних частот. В схеме ФВЧ меняются местами катушка индуктивности и конденсатор. Для ненагруженного ФВЧ получается следующий коэффициент передачи:
![]() .
.
На очень низких частотах модуль коэффициента передачи ФВЧ близок к нулю. На очень высоких — к единице. Характеристическое сопротивление определяется по той же формуле. Амплитудно-частотная характеристика ФВЧ представлена Рис.13.

Рис.13 – Амплитудно-частотная характеристика ФВЧ
