МВ Економетрія 2008 Доля

Вони, в свою чергу, використовуються для розрахунку дисперсій змінних за формулою (4.4), наприклад

Dр = 92,9871 – 89,1684 = 3,8187.

Крок 6. Для розрахунку коефіцієнтів кореляції необхідно попередньо виконати розрахунок середніх добутків змінних (табл. 4.5),

Таблиця 4.5 – Розрахунок середніх добутків змінних

після чого виконати розрахунок коефіцієнтів кореляції за формулою для варіанта Р=f (Ф, К):

Аналогічно rрк = 0,8178 і rрф = 0,5533.

Коефіцієнти кореляції показують напрямок і силу впливу факторів на рентабельність («+» – доданий, «–» – від’ємний). Слід мати на увазі, що −1 ≤ rpхі ≤ +1 . За наслідками розрахунків зробіть висновки щодо

сили (тісноти) кореляційних зв’язків.

Крок 7. Тестування факторів на значущість (невипадковість)

їх впливу на рентабельність проводять за t– статистикою Стьюдента. Розраховують спочатку вибіркові значення tі за формулою (для варі-

і потім порівнюють їх з критеріальним (tкрит). tкрит визначають за додатком 3 (див. [4], с. 87) залежно від n.

З ймовірністю 0,95 зробіть Ваші висновки щодо значущості факторів. При відсутності посібника можна прийняти tкрит = 2,179. У нашому прикладі за формулою (4.8)

21

і відповідно tк = 4,923. Отже вплив факторів на рентабельність є неви-

падковим, оскільки 6,405 > 2,179 і 4,923 > 2,179.

Крок 8. Наявність і сила мультиколінеарності факторів, тобто взаємозв'язку між ними оцінюється за повною матрицею коефіцієнтів кореляції

за наступною шкалою оцінок (за модулями коефіцієнтів кореляції для загального випадку y = f ( X1, X 2 ) :

r12 = 0 – відсутня,

Крок 9. β-коефіцієнти, які визначають напрямок і силу впливу факторів на рентабельність за умови вилучення мультиколінеарності, розраховують за формулою

22

Аналогічно βк = 0,4772.

Крок 10. Оцінка незалежності (автономності) впливу факторів

на рентабельність визначається за допомогою γ-критерія

0 < γi < 1 ,

Якщо γi > 0, фактор хi має певну автономність впливу на рентабельність; γi = 0 – ніякої автономності він не має і його вплив на рентабельність завдяки мультиколінеарності проявляється через інші фактори, якщо γ i < 0 – і-й фактор вилучається з подальшого процесу розробки рівняння регресії, бо знаки βi і rpxi протилежні, чого у належно специ-

фікованих моделях не може бути.

Крок 11. Розрахунок коефіцієнта множинної кореляції необхідний для визначення сили впливу на рентабельність обох факторів разом, він розраховується за формулою Боярського:

де α – порядок повної матриці коефіцієнтів кореляції; * – визначник повної матриці коефіцієнтів кореляції із за-

міною нижнього правого елемента нулем.

У нашому прикладі формула Боярського застосовується так:

=0,9317 = 0,9652.

Зметою контролю правильності розрахунків рекомендується цей коефіцієнт визначати також за такою формулою:

23

У прикладі (див. крок 9).

R рфк = 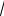0,8796 ´ 0,6155 + 0,8178 ´ 0,4772 = 0,5414 + 0,3903 =

= 0,9317 = 0,9652.

Отже коефіцієнт множинної детермінації і апроксимації 0,9317 показує, що варіація рентабельності у різних підприємств пояснюється впливом різних рівнів фондоозброєності праці на 54,14%, різного рівня кооперування виробництва на 39,03% та іншими не врахованими факто-

рами – 6,83% (100 – 83,17).

Крок 12. Вагомість вкладу факторів у варіацію рентабельності оцінюється на основі коефіцієнтів множинної кореляції за ρ-критерієм

ρi ³ 1,96,

У нашому прикладі формула (4.13) для визначення ρф і ρк набуває такого вигляду:

ρф = 0,742n R 2рфк - rрк2 ;

ρк = 0,742n R2рфк - rрф2 .

Якщо ρі ³ 1,96, то з ймовірністю 0,95 і більше можна стверджувати, що вплив фактора хі достатньо значущий, вагомий для включення його у рівняння регресії (див. [4], додаток 1, с. 85).

Крок 13. Для прийняття рішення щодо включення факторів у рівняння регресії складається зведення результатів, одержаних на кро-

ках 7, 10, 12 (табл. 4.6).

Таблиця 4.6. – Зведення оцінок невипадковості автономності й значущості вкладу факторів

24

Поради щодо прийняття рішень такі:

· якщо γ i < 0 , хi вилучається з матриці (див. крок 10);

·значення ρі дуже залежать від обсягу вибірки (див. формулу 4.13), тому рішення приймається з огляду на порушення вимоги n /(m +1) ³ 8 .

Отже якщо критерії ρі виконуються не в повній мірі, обидва фактори треба включати до рівняння регресії, принаймні з ймовірністю дещо менше 0,95.

Крок 14. Для обґрунтування аналітичної форми рівняння регресії

необхідно скористатися раніше сформульованими щодо цього висновками з теоретичного обґрунтування (див. крок 1), а також із візуального аналізу полів кореляції (див. крок 4). Ці аргументи вибору аналітичної форми рівняння регресії (пряма, гіпербола, парабола тощо) достатньо надійні й ними можна обмежитися.

Не буде великої помилки, якщо форма регресії буде прийнята лінійною і модель рівняння регресії матиме такий вигляд (для нашого прикладу):

де а0 , а1, а2 – коефіцієнти регресії.

Коефіцієнт а0 показує частину Р , що не залежить від факторів Ф і К ; а1 визначає, на скільки копійок змінюється Р за рахунок зміни Ф на одну тисячу гривень; а2 визначає зміну Р в копійках при зміні К на один відсоток.

Крок 15. Для розрахунку коефіцієнтів регресії а0 , а1 та а2 методом

найменших квадратів (МНК) слід скласти систему нормальних рівнянь і вирішити її. У нашому прикладі в разі вибору лінійної форми регресії ця система така:

Числові значення коефіцієнтів цієї системи беруть із табл. 4.4 (крок 5), та 4.5 (крок 6). У нашому прикладі система набуває вигляду

132,2 = 14а0 + 63,7а1 + 837а2, 654,39 = 63,7а0 + 357,43а1 + 4026,9а2, 8191,0 = 837а0 + 4026,9а1 + 52349а2.

25

Спосіб Гаусса полягає у послідовному вилученні невідомих а0, а1, та а2. Діленням системи на числові коефіцієнти при а0 отримаємо

9,4429 = а0 + 4,5500а1 + 59,7857а2,

10,2730 = а0 + 5,6115а1 + 63,2166а2,

9,7861 = а0 + 4,8111а1 + 62,5436а2.

Віднімемо 1-е рівняння із 2-го і 3-го, після чого маємо

0,8301 = 1,0615а1 + 3,4304а2,

0,3432 = 0,2611а1 + 2,7579а2.

тобто систему рівнянь без а0. Повторивши, цю саму процедуру ще раз, отримаємо одне рівняння з одним невідомим а2:

0,5324=7,3309а2,

звідки а2 = 0,0726. Далі зворотним шляхом знайдемо а1 = 0,5476 і а0 = 2,6108. Отже

Рˆ = 2,6108 + 0,5476Ф + 0,0726К.

Прокоментуйте сутність знайдених параметрів економетричної моделі рентабельності, тобто 2,6108; 0,5476 та 0,0726.

Крок 16. Для розрахунку коефіцієнтів регресії методом детер-

мінантів попередньо необхідно за системою рівнянь МНК визначити чотири детермінанта (визначника) – ∆А; ∆А0; ∆А1 і ∆А2. Зокрема у нашому прикладі це виглядає так:

Послідовно замінюючи стовпці матриці А стовпцями вільних членів системи рівнянь за МНК знайдемо

26

Оскільки розрахунки детермінантів виконуються вручну на калькуляторі, нагадуємо, як їх зручніше і простіше виконувати.

Елементи матриці А поділимо на 100,тобто на 102, що потім обумовить множення результату на 1000000, тобто на 106. Для розрахунку визначника матриці 3-го порядку допишемо до неї ще раз перші два рядки. Знайдемо добутки трьох елементів по кожній нісхідній діагоналі матриці (додатні) і такі ж добутки по висхідним діагоналям (від’ємні). Сумуючи шість добутків знаходимо детермінант. Наприклад

З урахуванням наведених раніше зауважень маємо ∆А = 1,513628 × 10 6 = 1513628.

Параметри рівняння регресії способом детермінантів отримуємо за формулою

тобто

а0 = 3951780 : 1513628 = 2,6108;

а1 = 828831 : 1513628 = 0,5476;

а2 = 109889 : 1513628 = 0,0726.

Значення параметрів ідентичні, як і сподівалось, отриманим способом Гаусса (крок 15).

Крок 17. Найбільш ефективним є розрахунок коефіцієнтів регресії способом оберненої матриці. Цей спосіб вигідний тим, що одночасно вирішує завдання визначення помилок оцінки коефіцієнтів регресії (крок 24) і апроксимації або прогнозу залежної змінної (крок 25), чого неможливо зробити інакше.

Спочатку отримуємо матрицю А-1, обернену до матриці А, тобто

27

Попередньо знайдемо мінори і алгебраїчні доповнення до кожного елемента матриці А і складемо матрицю [∆Aij]. Наприклад, алгебраїчне доповнення до елемента 14 складе

До речі, індикатори знаків мінорів для матриці 3-го порядку такі:

На основі матриці алгебраїчних доповнень

за формулою (4.17) розрахуємо обернену матрицю

Параметри рівняння регресії знаходимо за формулою

28

Отже маємо

а0 = 1,648475 × 32,2 + 0,023711 × 654,39 − 0,028183 × 8191 = 2,6108 ;

а1 = 0,023711 ×132,2 + 0,021353 × 654,39 − 0,002022 × 8191 = 0,5476 ;

а2 = −0,028183 ×132,2 − 0,002022 × 654,39 + 0,000625 × 8191 = 0,0726,

що ідентично отриманим раніше результатам.

Крок 18. Для контролю правильності розрахунків коефіцієнтів регресії рекомендується ще варіант їх розрахунку через β-коефіцієнти, а саме:

Цей спосіб можливий лише за умови, що обидва фактори включені до рівняння регресії (див. підрозділ 4.5).

Отже за формулами (4.19) отримуємо уже відомі нам значення коефіцієнтів регресії

а0 = 9,4429 − 0,5476 × 4,5500 − 0,0726 × 59,7857 = 2,6108 .

Крок 19. Розрахунок оцінок рентабельності за рівнянням регресії необхідний для визначення помилок апроксимації. Розрахунки доцільно внести до табл. 4.7.

Таблиця 4.7 – Розрахунок оцінок рентабельності й помилок апроксимації

29

За розрахунком ∑е2j = 3,6164. Отже дисперсія залишків De дорівнює

3,6164 / 14 = 0,2603, що складає 6,83% загальної дисперсії 3,8187 (крок 5).

Порівняйте цей результат з результатами кроку 11.

Крок 20. Тестування гомоскедастичності залишків еj, полягає в перевірці того, що De = const. Це одне з основних припущень правомірності застосування МНК.

Використаємо тест рангової кореляції Спірмана:

Розрахунок ∑d 2 для нашого прикладу фрагментарно наведено

втабл. 4.8.

Таблиця 4.8 – Розрахунок ∑d 2

і не перевищує tкрит = 2,179 (див. [4] додаток 3), то з ймовірністю більшою 0,95 можна стверджувати, що залишки еj гомоскедастичні і явище

гетероскедастичності відсутнє.

Крок 21. Тестування відсутності автокореляції залишків еj вико-

нується за тестом DW-Дарбіна-Уотсона:

30