2.2 Визначення координат точки оберненою кутовою засічкою

Початкові дані.

Координати початкових пунктів :

Х1 = 193,910 м ; Х2 = 216,301 м ; Х3 = 236,601 м.

Y1 = 182,151 м ; Y2 = 181,772 м ; Y3 = 181,452 м.

Значення виміряних кутів:

Варіант 1 : 1 = 43⁰ 59¹00¹¹ , 2 = 30⁰07¹00¹¹.

Варіант 2: 1 = 30⁰ 58¹ 00¹¹, 2 = 40⁰18¹00¹¹.

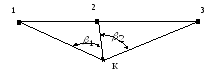
Рисунок - Схема зворотної кутової засічки.

Послідовність виконання роботи.

2. Обчислити координати пункту по формулах:

m = X1 + (Y1 - Y2) ctgв1 ;

n = Y1 + (X2 - X1) ctgв1 ;

^;

^;

^:

^;

де X1, Y1, X2, Y2, X3, Y3 - координати початкових пунктів, нумерація яких повинна зростати по ходу годинникової стрілки щодо пункту, координати якого визначаються;

β₁, β₂ – виміряні кути.

2.3. Оцінка точності визначуваного пункту к по формулах:

ΔΥ₁ = Υ₁ - Υ_Κ ; ΔΥ₂ = Υ₂ - Υ_Κ ; ΔΥ₃ = Υ₃ - Υ_Κ ;

ΔY₁ = Y₁ - Yk; ΔY₂ = Y₂ - Yk; ΔY₃ = Y₃ - Yk;

S= ΔX+ ΔY; S= ΔX+ ΔY; S= ΔX+ ΔY;

MK =

де m_β - середня квадратична погрішність вимірювання кутів теодолітом.

При обчисленні коефіцієнтів а і b лінійні величини S, ΔX, ΔY достатньо визначати повністю до 1 м.

2.4. Викреслити схему засічки в масштабі 1:1000 (або 1:2000, з нанесенням координатної сітки).

3 . Побудова еліпса похибок положення пункту, що визначається

3.1 Еліпс похибок найповніше і строго характеризує точність положення пункту.

Елементи еліпса погрішностей (рис.2) обчислюються по наступних формулах:

tg 2Θ = (4)

q = (5)

А =

B = ; (6)

, (7)

де Θ - дирекційний кут великої осі еліпса похибок;

А і В - відповідно велика і мала напівосі еліпса, м;

М_Н - середня похибка (зсув) пункту по заданому напряму, м;

α - дирекційний кут цього напрямку;

- кут між великою напіввіссю еліпса і даним напрямом.

3.2. Послідовність виконання роботи.

Для пункту, координати якого визначені кутовою засічкою побудувати еліпс похибок в наступному порядку:

- по формулах (3) визначити кореляційний момент К_ХУ і погрішності К_ХХ і К_YY;

- по формулах (5) - (7) обчислити елементи еліпса похибок;

- по одній з формул (6) визначите положення двох-трьох проміжних точок еліпса (які не лежать на його осях) з інтервалом 20-25⁰;

- викресліти еліпс похибок у масштабі 1:2 (або 1:3).

Креслення еліпса можна сумістити із схемою зворотної засічки.

Таблиця 1 Обчислення координат у зворотній кутовій засічці

№	Параметр	Значення	№	Параметр	Значення
1	Х1	193,910 м	17	ctgβ2	1,7239348
2	Y1	182,151	18	(15)х(17)	-0,552
3	Y2	181,772	19	(18) - Х3	-237,153
4	(Y1 – Y2)	+0,379	20	(19) + m (чисельн)	-42,851
5	tgβ1	0,96512677	21	Х3 - Х2	+20,300
6	ctgβ1	1,0361341	22	(22) х ctgβ2	+34,995
7	(Y1 – Y2) ctgβ1	+0,392	23	(21)+ Y3 – n (знамен)	+11,097
8	m	194,302	24	= (20) / (23)	-3,861494
9	X2	216,301	25		-21,999
10	(X2 – X1)	+22,391	26		+23,597
11	(X2 – X1) ctgβ1	+23,200	27		-91,050
12	n	205,351	28		15,910
13	Х3	236,601	29		-7,105
14	Y3	181,452	30		+27,436
15	Y3-Y2	-0,320	31		209,196
16	tgβ2	0,5800684	32		209,207

Таблиця 2 Оцінка точності у зворотній кутовій засічці

№	Параметр	Значення	№	Параметр	Значення
1	ХК	209	20	ΔХ23	729
2	YK	209	21	ΔY3	-28
3	Х1	194	22	ΔY23	784
4	Y1	182	23	S23	1523
5	Х2	216	24	А1	-0,028019
6	Y2	182	25	А2	-0,034150
7	Х3	237	26	А3	-0,018219
8	Y3	181	27	В1	-0,015828
9	ΔХ1	-15	28	В2	+0,008846
10	ΔХ21	225	29	В3	+0,018014
11	ΔY1	-27	30		+0,006130
12	ΔY21	729	31		-0,024674
13	S21	966	32		+0,015931
14	ΔХ2	+7	33		0,0091676
15	ΔХ22	49	34		6875
16	ΔY2	-27	35		+0,000056197
17	ΔY22	729	36		-0,00039308
18	S	803	37		0,000449

Продовження таблиці

19	ΔХ3	+27	38	=(34) (37)	3,089
39		9,54	49	(48)	0,00003052
40		0,0006088	50		-0,000151
41		0,0000842	51		+0,000146
42	(40)+(41)	0,0006920	52	(50+(51)	+0,0000050
43	= (42)/ (39)	0,0000726	53	(52)/ (39)	0,000000524
44		0,0000726		MK =	0,010м
45		0,0000375	55		0,0085м
46		0,0002537	56		0,0055м
47	(45)+(46)	0,0002912	57
48	(47/ (39)	0,00003052	58

Таблиця 3 Визначення елементів еліпса похибок

№	Параметр	Значення	№	Параметр	Значення
1		0,0000726	14		0,5000
2		0,000000524	15	А2	0,00007225
3		0,00003052	16		0,00003612
4		0,000001048	17		0,707107
5		0,000042076	18		0,5000
6	(4)2	1,098х 10 -12	19	В2	0,00003136
7	(5)2	1х 10 -9	20		0,00001568
8		0,0000408	21		0,0072м
9		0,00010312	22		0,0249073
10	(8)+(9)	0,00014392	23		1,4260
11		0,0085м	24		00,713
12		0,0056м
13		0,707107

Рисунок - Схема побудови еліпсу похибок

Рисунок - Елементи еліпса похибок.

3.3 Спрощена оцінка точності оберненої кутової засічки

Рисунок - До спрощеної оцінки точностї

Середню квадратичну похибку визначення положення точки зворотною кутовою засічкою у РГР визначають за формулою :

Значення параметрів формули визначають графічно за схемою:

;22;20;31,1;28.3 ;39,1.

ПРИКЛАД

2.3. Визначення координат точки зворотною лінійною засічкою

У зворотній лінійній засічці початковими даними є координати пунктів 1 і 2; вимірюваними даними є відстані , (відносна помилка вимірювання відстаней ); визначувані дані - координати точки P.

Початкові дані:

Координати настінних пунктів розбивочної основи

X1 =193,910; X2 = 216,301; X3 =236,601;

Y1 = 182.151 ; Y2 = 181,772 ; Y3 = 181,450;

Виміряні відстані

S1 = 31.085 + ; S2 = 28.341 + ; S3 = 38.998 + ;

Рисунок - Схема лінійна засічки

Порядок рішення задачі

1. З рішення зворотної геодезичної задачі визначити:

1.1 значення базису засічки - відстань між настінними пунктами, до яких вимірювалися відстані ( 1 і 2 (або іншими по варіанту)

.

1.2 дирекційний кут базису засічки (або по варіанту):

1.2.1 обчислюють румб базису: ;

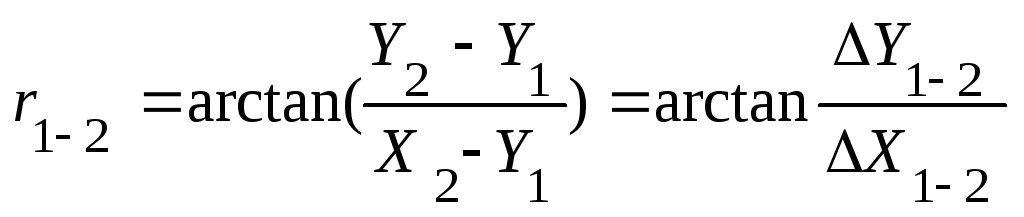1.2.2 по знаках приростів координат і визначають чверть, до якої відноситься румб, і обчислюють дирекційний кут, використовуючи залежність між дирекційними кутами і румбами

2. Виконати рішення трикутників 12Р ( або інших по варіанту) по формулах:

2.1 у трикутнику 12P по теоремі косинусів обчислити кути в1 і в2,

;

.

2.2 обчислити кут γ цього ж трикутника ;

2.3 обчислити дирекційні кути сторін 1Р і 2Р:

точка Р праворуч від лінії 1-2

; .

точка Р зліва від лінії 1-2

;

3. обчислити дирекційний кут напряму 2-1 :

;

4. вирішити прямі геодезичні задачі:

4.1 з пункту 1 на точку P

,

,

4.2 з пункту 2 на точку P

;

Таблиця - Рішення лінійної засічки

№	Параметр	Значення	№	Параметр	Значення
1		193,910	23		0,4773420
2		216,301	24		610.48805
3			25		600.51834
4		182,151	26		0,4921450
5		181,772	27		0,8705133
6			28		+ 15,298
7		+ 22,391	29		+ 27,059
8		- 0,379	30		209,209
9	(7)2	501,35688	31		209,210
10	(8)2	0,143641	32		1790.0302
11		22,394	33	-	-163,0595
12		501,4912	34	(33)+(12)	338,4317
13		31,084	35		1269,29
14		966,2151	36		0,2666307
15		28,340	37		740.5361
16		803,1556	38		10404942
17		- 0,01692643	39		-0,250281
18		Пн-Зх : 00,96972	40		0,9681730
19		3590,0302	41		-7,093
20		1392,190	42		+27,438
21	-	163,0595	43		209,208
22	(21)+(12)	664,5507	44		209,210

Допустима розбіжність координат і по двох рішеннях 0,010 м;

Розбіжність координат і по двох рішеннях не перевищує 0,005 м;

5. Оцінка точності

5.5 Помилку положення точки P у РГР обчислюють по формулі:

м ;м

43⁰.976

=0,694356 ; 0,0123м