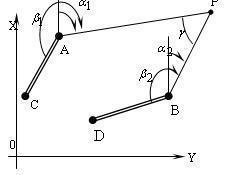
- •1.3.3 Пряма кутова засічка
- •7. Виконують перерахунок координат з системи в систему :
- •2. Створення геодезичної знімальної мережі засічками
- •1. Визначення планового положення точки р
- •1.1Польові (вимірювальні роботи)
- •1.2 Обчислення перевищення між точками базиса 1 і 2 та точкою р
- •2. Оцінка точності результатів вимірювань у елементарних процесах
- •2.1 Визначення координат точки прямою кутовою засічкою ( при відомих координатах пунктів базису)
- •2.2.1 Оцінка точності прямої засічки:
- •2.2 Визначення координат точки оберненою кутовою засічкою
- •2.3. Оцінка точності визначуваного пункту к по формулах:
- •2.4 Визначення положення точки у створі
ТЕОРЕТИЧНІ ЗАСАДИ ЗАСТОСУВАННЯ ЗАСІЧОК
ДЛЯ ВИЗНАЧЕННЯ КООРДИНАТ ТОЧОК ЗНІМАЛЬНОЇ ОСНОВИ
1.1 Пряма і зворотна геодезичні задачі
У основі різноманітних методів геодезичних побудов і алгоритмів рішення багатьох інженерно-геодезичних задач лежать дві стандартні задачі на площині: пряма і зворотна геодезична задачі
1.1.1 Пряма геодезична задача (рис. 1 )
Початкові
дані : координати
першого пункту![]() ,
,
![]() ,
, дирекційний кут
,
, дирекційний кут
![]() лінії 1- 2 і довжина
лінії 1- 2 і довжина
![]() лінії 1-2, яка сполучає початковий 1 і
визначуваний 2 пункти.
лінії 1-2, яка сполучає початковий 1 і
визначуваний 2 пункти.
Визначувані
величини:
координати![]() ,
,![]() ,
другого пункту.
,
другого пункту.
Рішення прямої геодезичної задачі
Координати другої точки визначають за формулами (1)
![]() ,
,
![]() .
(1)
.
(1)
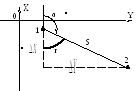
Рисунок 1 - Схема геодезичних задач
1.1.2 Зворотна геодезична задача (рис. 1).
Початкові
дані:
два пункти з відомими координатами
![]() і
і
![]()
Визначувані
величини:
дирекційний кут
![]() і довжина лінії
і довжина лінії![]() ,
що сполучає 1 і 2.
,
що сполучає 1 і 2.
Рішення зворотної геодезичної задачі
Рішення зворотної геодезичної задачі має декілька варіантів , воно складніше, що повязане з особливостями використання тригонометричих функцій.
Вариант1
Якщо![]() і
і
![]() , то трикутник розв'язується по формулах:
, то трикутник розв'язується по формулах:
![]()
![]() ;
і
;
і
![]() .
.
Порядок визначення дирекційного кута лінії:
-
по знаках приростів координат
![]() визначити номер чверті;
визначити номер чверті;
- по формулах зв'язку дирекційних кутів і румбів відповідно до номера чверті обчислити дирекційний кут .
Контролем правильності обчислень є виконання умов:
![]() .
.
Якщо![]() ,
то ,
,
то ,
![]()
![]() при
при
![]() ;
;
![]() при
при
![]() .
.
Якщо
![]() , то
, то![]()
![]() при
при![]() ;
;
![]() при
при
![]() .
.
Варіант 2
Використовується
алгоритм, що виключає можливе ділення
на нуль при
![]() :
:
![]() ,
,
![]() .
.
Якщо![]() , то
, то![]() ; якщо
; якщо
![]() , то
, то
![]() .
.
.
Для однозначного визначення на місцевості точки P потрібно виконати побудову двох елементів.
Комбінації двох елементарних побудов для визначення точки на площині називаються геодезичними засічками.
3.5 Підготовка розмічувальних креслень
Розмічування точок засічкми
Можливі варіанти засічок
1. Полярна засічка - будується один кут і відкладається одна відстань; обидві побудови виконуються від пункту А.
2. Пряма кутова засічка - вимірюються два кути; один кут вимірюється на пункті А, інший - на пункті B.
3. Лінійна засічка - вимірюються дві відстані; одна відстань - від пункту А до пункту P, інше - від пункту B до пункту P.
4. Зворотна кутова засічка - обидва вимірювання виконуються на точці P. Вимірюються два кути: один кут між напрямами на початкові пункти А і B, інший - між напрямами на початкові пункти B і D.
1.3.2 Полярна засічка
Початкові
дані:
координати пункту А і дирекційний кут![]() напряму АВ, середня квадратична похибка
вимірювання кута
напряму АВ, середня квадратична похибка
вимірювання кута
![]() і відносна похибка вимірювання відстані
і відносна похибка вимірювання відстані
![]() .
(Якщо дирекційний кут
.
(Якщо дирекційний кут
![]() не заданий, його обчислюють рішенням
зворотної геодезичної задачі між
пунктами А і В)
не заданий, його обчислюють рішенням
зворотної геодезичної задачі між
пунктами А і В)
Вимірювані
величини:
горизонтальний кут![]() і відстань
і відстань![]() .
.
Визначувані величини : координати точки P.
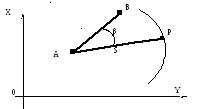
Рисунок 4 - Схема полярної засічки
Послідовність рішення полярної засічки:
-обчислити дирекційний кут лінії АР :
![]() ;
;
- обчислити прирости координат:
![]() ;
;
![]() ;
;
- обчислити координати точки P:
![]() ;
;
![]() ;
;
- обчислити похибку положення точки P:
![]() ;
;
де
![]() -
середня квадратична погрішність
вимірювання кута,
-
середня квадратична погрішність
вимірювання кута,
![]() -
відносна похибка вимірювання відстані
, ρ = 206265".
-
відносна похибка вимірювання відстані
, ρ = 206265".
1.3.3 Пряма кутова засічка
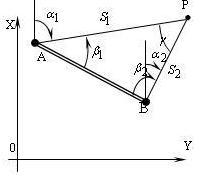
1.Загальний випадок прямої кутової засічки
Вимірюються
кути
![]() і
і
![]() на двох пунктах з відомими координатами,
кожен від свого напряму з відомим
дирекційним кутом (рис. 5 ).
на двох пунктах з відомими координатами,
кожен від свого напряму з відомим
дирекційним кутом (рис. 5 ).
Початкові
дані:
![]() ;
;
Вимірювані
величини:
![]() і
і
![]() (обидва кути - ліві);
(обидва кути - ліві);
Визначувані величини: координати точки Р .
Якщо
![]() або
або
![]() не задані явно, потрібно вирішити
зворотну геодезичну задачу спочатку
між пунктами А і С і потім між пунктами
B і D .
не задані явно, потрібно вирішити
зворотну геодезичну задачу спочатку
між пунктами А і С і потім між пунктами
B і D .
|
|
|
Рисунок 5 - Пряма кутова засічка
Послідовність рішення прямої кутової засічки:
-
обчислити дирекційні кути ліній АР (![]() )
і BP (
)
і BP (![]() ):
):
![]() ;
;
![]() ;
;
- скласти рівняння прямих ліній АР і ВР:
![]() ,
,
![]() ;
;
- вирішити систему рівнянь і обчислити невідомі координати
![]() ,
,
![]() .
.
2. Окремий випадок прямої кутової засічки
Кути
![]() і
і
![]() зміряні
від напрямів AB і BA. При цьому кут
зміряні
від напрямів AB і BA. При цьому кут
![]() - правий, а кут
- правий, а кут
![]() - лівий (рис. ).
- лівий (рис. ).
Послідовність рішення прямої кутової засічки методом трикутника (окремий випадок засічки):
-
вирішити зворотну задачу між пунктами
А і B і визначити дирекційний кут
![]() і
довжину
і
довжину
![]() лінії AB,
лінії AB,
-
обчислити кут
![]() при вершині P
при вершині P
![]() ;
;
-
для трикутника APB по теоремі синусів
обчислити довжини сторін АР (![]() )
і BP (
)
і BP (![]() ):
):
![]() ,
,
-
обчислити дирекційні кути
![]() і
і
![]()
![]() ,
,
![]() ;
;
- вирішити пряму задачу від пункту А на точку P.
- для контролю - вирішити пряму задачу від пункту B до точки P ;
Контроль: обидва рішення повинні співпасти.
У окремому випадку прямої кутової засічки для обчислення координат можна використовувати формули Юнга:
![]() ,
,
![]()
Для переходу від загального випадку прямої кутової засічки до окремого випадку потрібно:
-
вирішити зворотну геодезичну задачу
між пунктами А і B і одержати дирекційний
кут
![]() лінії AB.
лінії AB.
- обчислити кути в трикутнику APB при вершинах А і B:
![]() ;
;
![]() .
.
При комп'ютерному рішенні:
1)
обчислити дирекційні кути
![]() і
і
![]() ,
,
2)
ввести місцеву системи координат
![]() з початком в пункті А і з віссю
з початком в пункті А і з віссю![]() ,
направленою по лінії АР.
,
направленою по лінії АР.
3)
виконати перерахунок координат пунктів
А і B і дирекційних кутів
![]() і
і![]() з системи
з системи
![]() в систему
в систему
![]() (рис. )
(рис. )
![]() ;
;
![]() ;
;![]()
![]() ;
;![]() ;
;
![]() ;
;
![]()
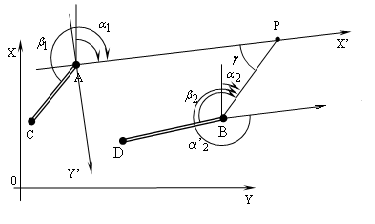
Рисунок
6 - Пряма кутова засічка в системі
координат
![]()
4)
представити рівняння ліній АР і BP в
системі
![]()
![]() ,
,
![]() ;
;
5) сумісне рішення цих рівнянь
![]() ,
,
![]() ;
( 2)
;
( 2)
6)
перевести координати
![]() і
і![]() з системи
з системи
![]() в систему
в систему
![]()
![]() ,
,
![]() .
.
Оскільки
![]() і кут засічки
і кут засічки
![]() завжди більше
завжди більше![]() , то рішення (2) завжди існує!.
, то рішення (2) завжди існує!.
1.3.4 Лінійна засічка
Початкові
дані:
координати пунктів А і В, (відносна
похибка вимірювання відстаней
![]() );
);
Вимірювані
величини:
відстані
![]() і
і
![]() ;
;
Визначувані
величини
- координати
![]() точки
P.
точки
P.
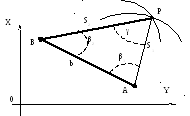
Рисунок 7 - Лінійна засічка
Можливі варіанти рішення лінійної засічки.
Варіант 1 (при рішенні на ЕОМ).
1. Виконується рішення системи рівнянь двох зміряних відстаней:
![]() ,
,
![]() .
.
2.
Оскільки ця системи рівнянь не має
простого рішення в системі координат
![]() ,
застосовують систему координат
,
застосовують систему координат ![]() з початком в точці А і віссю
з початком в точці А і віссю![]() . Ця вісь направлена від точки А уздовж
лінії АВ.
Координати точок А і В в новій системі:
. Ця вісь направлена від точки А уздовж
лінії АВ.
Координати точок А і В в новій системі:
![]()
![]()
![]()
![]()
3. Рішенням
зворотної геодезичної задачі між точками
А і В знаходять довжину лінії АВ=![]() .
.
4.
Обчислюють дирекційний кут ![]() лінії АВ також з рішення зворотної
геодезичної задачі.
лінії АВ також з рішення зворотної
геодезичної задачі.
5.
Задають і спільно вирішують рівняння
двох кіл в новій системі координат![]() :
:
![]() ;
;
![]() .
.
6. Визначувані координати:
![]() ,
,
![]() .
.
Якщо
шукана точка знаходиться зліва від
лінії АВ,
то у формулі для ![]() потрібно брати знак "мінус", якщо
справа, то - знак "плюс".
потрібно брати знак "мінус", якщо
справа, то - знак "плюс".