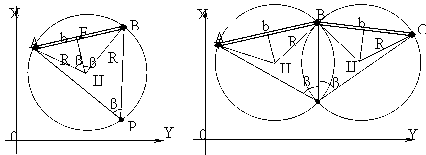
- •1.3.3 Пряма кутова засічка
- •7. Виконують перерахунок координат з системи в систему :
- •2. Створення геодезичної знімальної мережі засічками
- •1. Визначення планового положення точки р
- •1.1Польові (вимірювальні роботи)
- •1.2 Обчислення перевищення між точками базиса 1 і 2 та точкою р
- •2. Оцінка точності результатів вимірювань у елементарних процесах
- •2.1 Визначення координат точки прямою кутовою засічкою ( при відомих координатах пунктів базису)
- •2.2.1 Оцінка точності прямої засічки:
- •2.2 Визначення координат точки оберненою кутовою засічкою
- •2.3. Оцінка точності визначуваного пункту к по формулах:
- •2.4 Визначення положення точки у створі
7. Виконують перерахунок координат з системи в систему :
![]()
![]()
Варіант 2 (для "ручного обрахунку")
1. Обчислюють кути β1 і β2 рішенням трикутника АВР по теоремі косинусів:
![]() ,
,
![]() ;
;
2.
Обчислюють кут γ
цього ж трикутника
![]() ;
;
3. Обчислюють дирекційні кути сторін АР і BР:
- точка Р праворуч від лінії AB:
![]() ,
,
![]() .
.
- точка Р ліворуч від лінії AB:
![]() ,
,
![]()
4. З рішення зворотної геодезичної задачі між точками А і B визначають дирекційний кут αAB AB лінії АВ.
Дирекційний
кут лінії ВА:
![]() ;
;
5. Вирішують прямі геодезичні задачі:
- з пункту А на точку P:
![]() ,
,
![]() .
.
- з пункту B на точку P:
![]() ,
,
![]()
6.
Контроль:
розбіжність координат![]() і
і
![]() по
двох рішеннях не повинна перевищувати
0,02 м;
по
двох рішеннях не повинна перевищувати
0,02 м;
7. Похибку положення точки P по обчислюють формулі:
![]() ,
,
де![]() -
середні квадратичні похибки вимірювання
відповідних відстаней
-
середні квадратичні похибки вимірювання
відповідних відстаней
![]() -
кут засічки.
-
кут засічки.
.
1.3.5 Зворотна кутова засічка
Зворотною
кутовою засічкою називають спосіб
визначення координат точки по двох
кутах
![]() і
і![]() ,
зміряним на визначуваній точці між
напрямами на три пункти з відомими
координатами (рис. 5).
,
зміряним на визначуваній точці між
напрямами на три пункти з відомими
координатами (рис. 5).
Початкові
дані:
![]() ;
;
Вимірювані
величини:
![]() ;
;
Невідомі
величини:
координати точки Р -
![]() .
.
У
колі, що проходить через три точки![]() ,
кут з вершиною на колі
,
кут з вершиною на колі
![]() вимірюється половиною дуги АВ,
на яку він спирається. Центральний
кут, що спирається на ту ж дугу, вимірюється
всією дугою, отже, він буде дорівнювати
вимірюється половиною дуги АВ,
на яку він спирається. Центральний
кут, що спирається на ту ж дугу, вимірюється
всією дугою, отже, він буде дорівнювати
![]() (рис. ).
(рис. ).
|
|
|
а) до обчислення R і координат Ц
Рисунок 8 - Зворотна кутова засічка
Відстань
![]() між пунктами А і В вважається відомою.
Радіус кола знаходять і з прямокутного
трикутника
між пунктами А і В вважається відомою.
Радіус кола знаходять і з прямокутного
трикутника![]() :
:
![]() (3)
(3)
Рівняння кола має вигляд:
![]() ,
(4)
,
(4)
Координати центру кола можна обчислити, вирішивши пряму кутову, або лінійну засічку з пунктів А і В на точку Ц.
У рівнянні ( 4) - координати будь-якої точки кола, у тому числі і точки, але для знаходження двох координат точки одного такого рівняння недостатньо.
Рішення зворотної кутової засічки передбачає її розкладання на простіші задачі. Це можуть бути дві прямі кутові засічки і одна лінійна, або три лінійні засічки і т.д. Відомо більше десяти способів аналітичного рішення зворотної кутової засічки.
1.3.6 Рішення зворотної кутової засічки через послідовне рішення трьох лінійних засічок.
Приймаючи,
що положення точки Р відоме, можна
провести два кола: одну радіусом
![]() через точки
через точки
![]() і інше - радіусом
і інше - радіусом
![]() через точки
через точки
![]() (рис. ).
(рис. ).
Радіуси цих кіл :
![]() ;
;
![]() .
.
Якщо
координати центрів кіл (точок
![]() і
і![]() ) будуть відомі, то:
) будуть відомі, то:
- координати точки Р можна визначити по формулах лінійної засічки:
з
точки
![]() по відстані
по відстані
![]() і з точки
і з точки
![]() - по відстані
- по відстані![]() .
.
-
координати центру
![]() можна знайти по формулах лінійної
засічки з точок А і В по відстанях
можна знайти по формулах лінійної
засічки з точок А і В по відстанях![]() .
.
При
цьому, з двох рішень приймають відповідне
величині кута
![]() :
:
-
якщо
![]() ,
то точка знаходиться праворуч від лінії
АВ;
,
то точка знаходиться праворуч від лінії
АВ;
-
якщо![]() , то точка знаходиться ліворуч від лінії
АВ.
, то точка знаходиться ліворуч від лінії
АВ.
-
координати центра
![]() визначають
по формулах лінійної засічки з точок В
і С по відстанях
визначають
по формулах лінійної засічки з точок В
і С по відстанях![]() .
.
Одне з можливих рішень з двох вибирається за правилом:
-
![]() якщо,
то точка
якщо,
то точка
![]() знаходиться праворуч від лінії ВС ;
знаходиться праворуч від лінії ВС ;
-
![]() якщо
, то точка
якщо
, то точка
![]() знаходиться зліва від лінії ВС .
знаходиться зліва від лінії ВС .
Задача
не має рішення,
якщо всі чотири точки
![]() і Р
знаходяться на одному колі, оскільки
обидва кола зливаються в одну, і точку
їх перетину вказати неможливо.
і Р
знаходяться на одному колі, оскільки
обидва кола зливаються в одну, і точку
їх перетину вказати неможливо.
1.3.7 Комбіновані засічки
У розглянутих способах рішення засічок кількість вимірювань приймалася теоретично мінімальною (два вимірювання). Вона забезпечує отримання результату, але при цьому немає контролю правильності вимірювань.
На
практиці для знаходження координат
![]() і
і
![]() однієї точки, як правило, виконують не
два, а три і більш вимірювань. В цьому
випадку з'являється можливість контролю
вимірювань, і, крім того, підвищується
точність рішення задачі. Кожне вимірювання,
що вводиться в задачу понад теоретично
мінімальну кількість, називають
надлишковим. Воно створює одне додаткове
рішення.
однієї точки, як правило, виконують не
два, а три і більш вимірювань. В цьому
випадку з'являється можливість контролю
вимірювань, і, крім того, підвищується
точність рішення задачі. Кожне вимірювання,
що вводиться в задачу понад теоретично
мінімальну кількість, називають
надлишковим. Воно створює одне додаткове
рішення.
Геодезичні засічки без надлишкових вимірювань прийнято називати одноразовими.
Засічки з надлишковими вимірюваннями називають багаторазовими.
Наявність надмірних вимірювань дозволяють виконати їх математичну обробку - зрівнювання. Строге зрівнювання вимірювань в різних геодезичних побудовах виконується на ЕОМ;
Для ручного рахунку звичайно застосовують нестрогі (спрощені) способи зрівнювання.
Спрощений
спосіб зрівнювання якої-небудь
багатократної засічки (
![]() вимірювань)
передбачає:
вимірювань)
передбачає:
-
формування і рішення всіх можливих
варіантів незалежних одноразових
засічок (їх число рівне
![]() );
);
- обчислення середніх значень координат точки зі всіх одержаних результатів, якщо вони розрізняються між собою на допустиму величину.
1.4 Оцінка точності вимірювань
1.4.1 Похибка положення точки в одноразових засічок
Положення точки на площині по двох вимірюваннях виходить в перетині двох ліній положення.
Для
зміряної відстані
![]() лінією
положення
є коло радіусу
лінією
положення
є коло радіусу
![]() з центром в початковому пункті А (рис.
а).
з центром в початковому пункті А (рис.
а).
Для
зміряного кута
![]() з вершиною в початковому пункті А
- пряма лінія, проведена під кутом
з вершиною в початковому пункті А
- пряма лінія, проведена під кутом
![]() до початкової лінії АВ (рис. б).
до початкової лінії АВ (рис. б).
Унаслідок помилок вимірювань вводиться поняття "смуга положення".
Д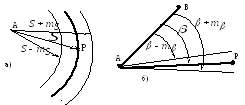 ля
відстані
ля
відстані![]() , зміряної з середньою квадратичною
помилкою
, зміряної з середньою квадратичною
помилкою
![]() - це круговий пояс (кільце) завширшки
- це круговий пояс (кільце) завширшки
![]() між двома колами радіусами
між двома колами радіусами
![]() і
і
![]() ;
;
а) для зміряної відстані, б) для зміряного кута.
Рисунок 9 - Лінія положення і "смуга положення" точки Р:
Для
кута![]() ,
зміряного з помилкою
,
зміряного з помилкою
![]() - це вузький трикутник з вершиною в
точці А і кутом при вершині
- це вузький трикутник з вершиною в
точці А і кутом при вершині![]() .
.
Лінія положення точки є віссю симетрії смуги положення (рис. 9б).
Вводиться так само поняття "вектор похибки вимірювання".
Він
позначений його через
![]() .
.
Для
зміряної відстані
вектор
![]() направлений уздовж лінії (прямо або
назад) і має модуль
направлений уздовж лінії (прямо або
назад) і має модуль![]() .
.
Для
зміряного кута
вектор
![]() направлений перпендикулярно лінії АР
(вліво або вправо від неї) і має модуль
:
направлений перпендикулярно лінії АР
(вліво або вправо від неї) і має модуль
:
![]() ,
,
де
![]() .
.
Точка Р, знаходячись на перетині двох ліній положення, є центром чотирикутника положення, що утворюється в перетині двох смуг положення (рис. 7). Цей елементарний чотирикутник можна вважати паралелограмом. В межах його дуги кіл можна замінити відрізками дотичних, а сторони кута, що розходяться, - відрізками прямих, паралельних лінії положення. Відстані від точки Р до меж чотирикутника неоднакові, що говорить про відмінність помилок положення точки Р по різних напрямах.
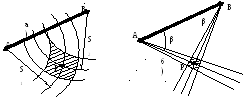
а) у лінійній засічці, б) у прямій кутовій засічці.
Рисунок 10 - Чотирикутник положення
Лінії положення ділять чотирикутник положення на 4 рівні частини (Рис. 10 ), які називають паралелограмами похибок з кутами при вершинах
![]() і
і![]() .
Кут між векторами помилок
.
Кут між векторами помилок
![]() і
і![]()
![]() ,
,
![]() .
.

Рисунок 11 - Паралелограми похибок
Висоти паралелограмів помилок чисельно рівні модулям векторів і , сторони паралелограмів одержують по :
![]() ;
;
![]() .
(5)
.
(5)
Найбільше ухилення від точки мають дві протилежні вершини паралелограма положення; дві інші вершини мають якнайменше ухилення.
У будь-якій геодезичній побудові існує так зване "найслабкіше місце". У цьому місці помилка якого-небудь елементу має найбільше значення. Як правило, для узагальненої характеристики точності даної побудови береться значення помилки саме в цьому найслабкішому місці.
Відповідно до цього принципу за помилку положення точки Р можна прийняти довжину великої діагоналі паралелограма похибок
![]()
або з урахуванням (5)
![]() .
.
Похибка положення точки Р - це скалярна величина, що показує середнє квадратичне відхилення по різних напрямах обчисленого положення точки від її істинного положення
![]()
З цієї формули одержано формули для оцінки точності будь-якої одноразової засічки:
- полярна засічка:
![]() ;
;
![]() ;
;![]() ;
;
![]()
![]() ;
;
- пряма кутова засічка:
![]() ;
;
![]() ;
;
- лінійна засічка :
![]() ;
;
![]() ;
;
![]()
- зворотна кутова засічка:
У цій засічка і права частина формули похибки положення точки Р повинна містити три складові:
- від похибки лінійної засічки точки Ц1 з початкових пунктів А і В ,
- від похибки лінійної засічки точки Ц2 и з початкових пунктів В і С ,
- від похибки лінійної засічки точки Р з точок Ц1 і Ц2.
У
практиці часто достатньо прийняти, що
істинне положення точки Р знаходиться
усередині кола радіусу
![]() з центром в точці Р .
з центром в точці Р .
У строгій теорії розглянутий критерій називається радіальною похибкою. Крім того, в цій теорії застосовуються і складніші критерії, такі як "еліпс помилок" (крива 2-го порядку), "подера еліпса помилок" (крива 4-го порядку) і ін.
При
кількості вимірювань
![]() (багатократні
засічки точка виходить в перетині
(багатократні
засічки точка виходить в перетині![]() ліній положення, відповідних зрівняним
значенням вимірювань. Смуги положення,
перетинаючись, утворюють
ліній положення, відповідних зрівняним
значенням вимірювань. Смуги положення,
перетинаючись, утворюють![]() -кутник.
Похибка положення точкиР
визначатиметься відстанню від точки
до найвіддаленішої від неї вершини
цього багатокутника.
-кутник.
Похибка положення точкиР
визначатиметься відстанню від точки
до найвіддаленішої від неї вершини
цього багатокутника.