Якщо ж a=b=c, то із (1) матимем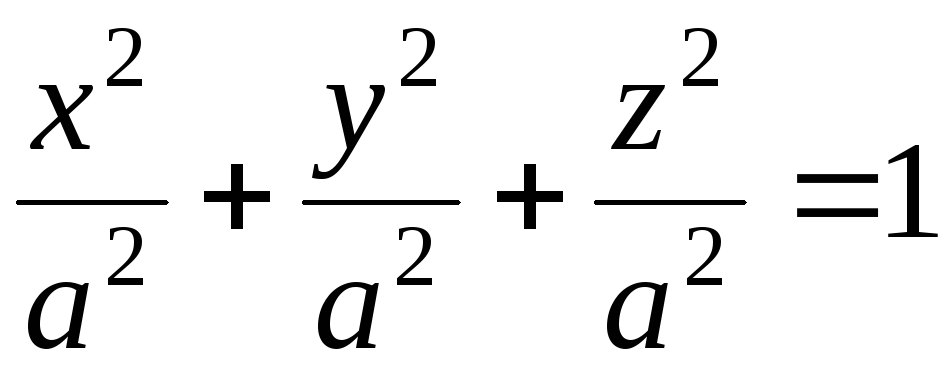о: , або.

Це рівняння сфери з центром у початку координат. Отже, сфера є частинним випадком еліпсоїда.

Справедлива й така теорема:

Т е о р е м а. При перетині еліпсоїда довільною площиною в перерізі утворюється еліпс.

Д о в е д е н н я.

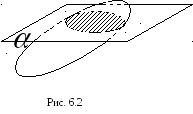Оскільки еліпсоїд є обмеженою поверхнею, то при перетині його з будь-якою площиною утвориться обмежена крива другого порядку (див. теорему із §1). Тому ця крива не може бути ні параболою, ні гіперболою, ні парою прямих. Отже, вона є еліпсом, що й треба було довести (рис. 6.2).

П р и к л а д. Записати рівняння еліпсоїда, осі якого збігаються з осями координат, і який проходить через точку та перетинає площинупо еліпсу

. (2)

Р о з в’ я з а н н я.

Якщо осі координат збігаються з осями еліпсоїда, то ця система координат є канонічною, тому рівняння еліпсоїда матиме вигляд:

. (3)

Площина перетинає цей еліпсоїд по еліпсу. Співставляючи останнє рівняння із (2) матимемо:. Тоді рівняння (3) набуде вигляду:.

За умовою точка лежить на цій поверхні, тому

,

звідки .

Тому рівняння даного еліпсоїда .

Відповідь: .

§7. Однопорожнинний гіперболоїд

Означення. Однопорожнинним гіперболоїдом називається поверхня, яка в деякій прямокутній системі координат задається рівнянням

. (1)

Це рівняння називається канонічним рівняннямоднопорожнинного гіперболоїда, а система координат, в якій воно задане, –канонічною системою координат.

Властивості однопорожнинного гіперболоїда

Аналізуючи рівняння (1), встановлюємо такі властивості даної поверхні:

1. Однопорожнинний гіперболоїд не проходить через початок координат.

2. Однопорожнинний гіперболоїд не перетинає вісь 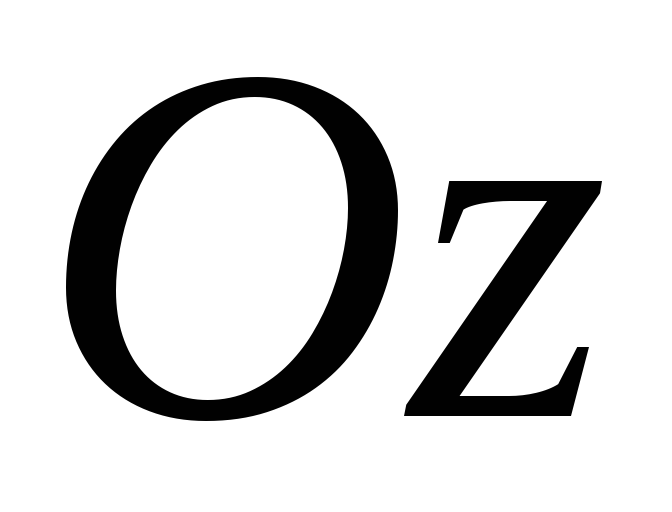, а дві інші осі перетинає в точках, симетричних відносно початку координат, а саме:

• вісь 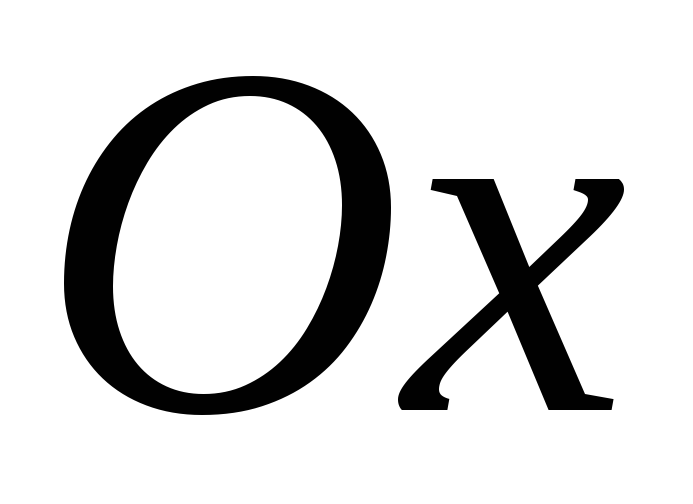у точках,

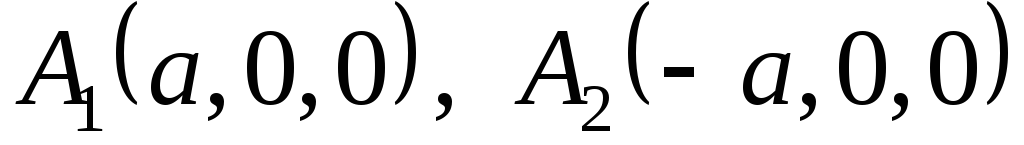• вісь 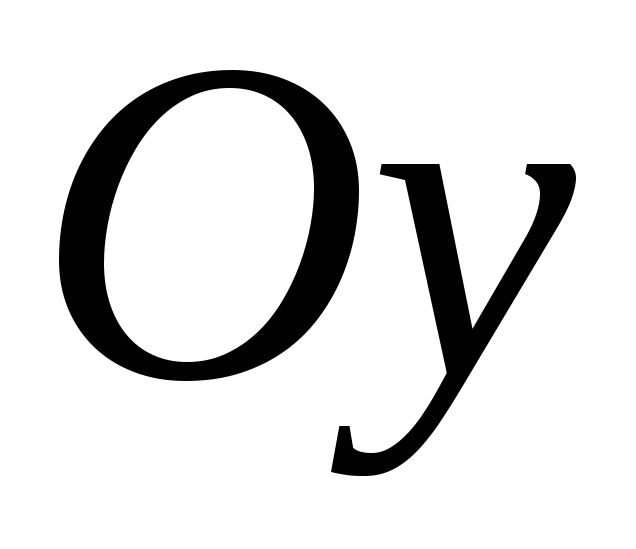у точках.

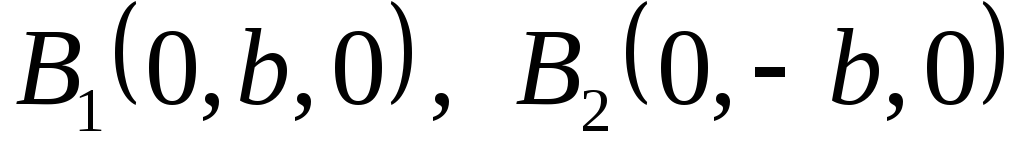Ці точки називаються вершинами однопорожнинного гіперболоїда, а відрізки – дійсними осями однопорожнинного гіперболоїда. Відрізокназивається його уявною віссю, числа– дійсними півосями,– уявною піввіссю.

3. Однопорожнинний гіперболоїд симетричний відносно всіх координатних площин, координатних осей і початку координат, оскільки всі змінні входять у його рівняння в парних степенях.

Вісь називаютьголовною віссюоднопорожнинного гіперболоїда.

4. Якщо дану поверхню перетнути площинами, паралельними до площини, то в перерізі утворяться еліпси, рівняння проекцій яких на площинумають вигляд

,

або

.

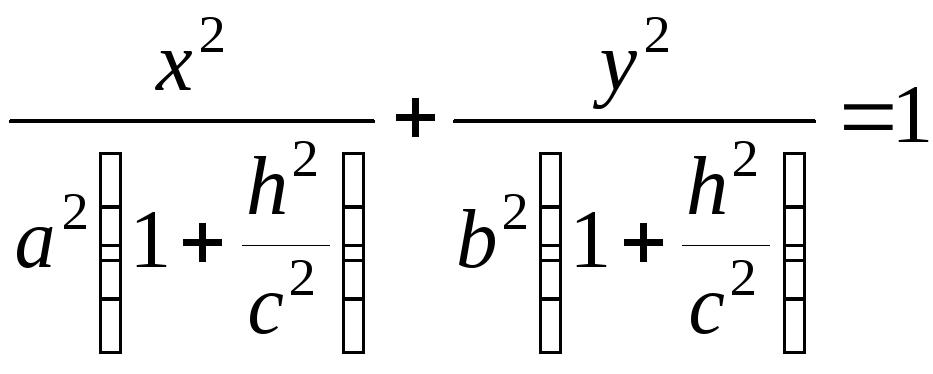Розміри цих еліпсів зростають із збільшенням .

Еліпс найменших розмірів утворюється при , тобто при перетині однопорожнинного гіперболоїда площиною. Рівняння цього еліпса. Він називаєтьсягорловим е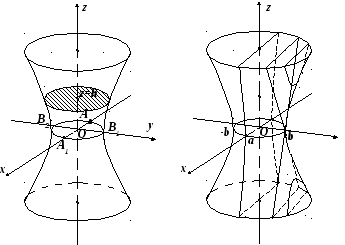ліпсомоднопорожнинного гіперболоїда (рис. 7.1).

Рис. 7.1 Рис. 7.2

Якщо однопорожнинний гіперболоїд перетнути площиною , де, то в перерізі утвориться гіпербола, рівняння проекції якої на площинумає вигляд:

,

або

.

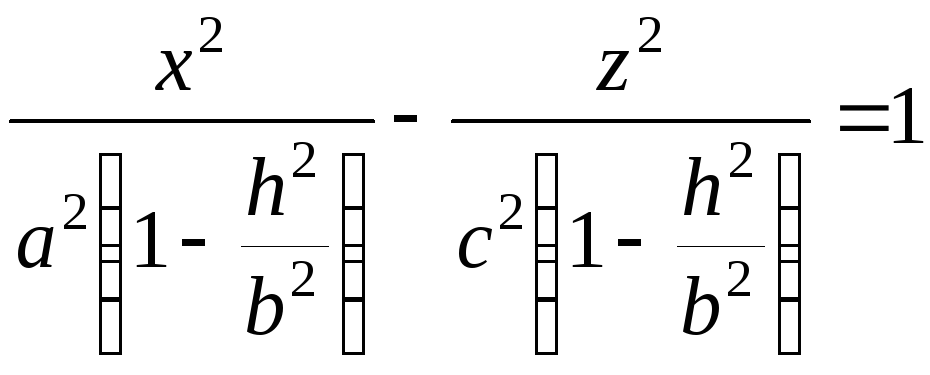Якщо , то уявною віссю такої гіперболи є вісь.

Якщо , то уявною віссю є вісь.

Якщо , то в перерізі утворяться дві прямі, що перетинаються:(рис. 7.2).

Аналогічні перерізи утворюються і при перетині однопорожнинного гіперболоїда площинами, паралельними до площини .

Розглянемо поряд з однопорожнинним гіперболоїдом (1) конічну поверхню, задану рівнянням

. (2)

Ця поверхня не перетинається з однопорожнинним гіперболоїдом, бо система рівнянь

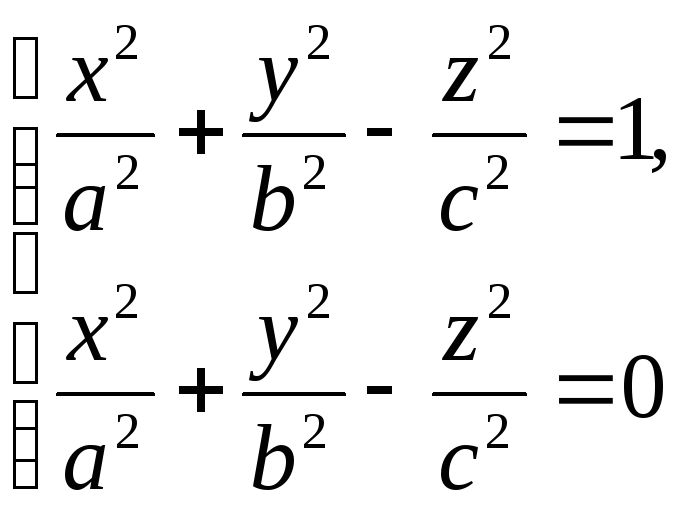
несумісна.

Оскільки цей конус проходить через початок координат, який міститься всередині однопорожнинного гіперболоїда, то і весь конус міститься всередині однопорожнинного гіперболоїда. Якщо обидві поверхні перетнути площиною , рівняння якої, то в перетині з гіперболоїдом отримаємо гіперболу

,

а в перетині з конусом – дві прямі: , які будуть асимптотами цієї гіперболи (рис. 7.3). Можна показати, що ця властивість конуса, пов’язана з однопорожнинним гіперболоїдом, залишається в силі і при перетині будь-якою іншою площиною, що проходить через вісь.

У зв’язку з цим даний конус називають асимптотичним конусом однопорожнинного гіперболоїда (рис. 7.4).

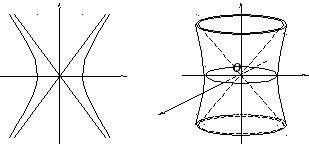z z

-a a x y

x

Рис. 7.3 Рис. 7.4

Рівняння ітакож задаютьоднопорожнинні гіперболоїди з головною віссю відповідно та.

П р и к л а д.Записати канонічне рівняння однопорожнин-ного гіперболоїда, якщо він перетинає площинупо колу, а площину– по гіперболі.

Р о з в’ я з а н н я.

Однопорожнинний гіперболоїд перетинає площину по колу, тому його головною віссю є вісь, а його рівняння має вигляд:

. (3)

Ця поверхня перетинається з площиною по еліпсу. Співставляючи з даною лінією перетину, або, отримаємо:.

Тоді рівняння (3) набуде виду: .