§ 3 Арифметичний n-вимірний векторний простір

1. Поняття про арифметичний n-вимірний векторний простір

Нехай Р – деяке числове поле.

Означення1. Кожна упорядкована система n чисел із числаР називається n-вимірним числовим вектором; числа називаються його координатами або компонентами.

Числові вектори будемо позначати:

Означення 2. Два числові вектори

і

будемо вважати рівними тоді і тільки тоді, коли рівні їх відповідні координати, тобто

Розглянемо тепер множину всіх n-вимірних числових векторів з координатами з поляР. Визначимо в цій множині операції додавання векторів і множення вектора із на число із поля Р.

Означення 3. Сумою векторівіназивається вектор.

Означення 4. Добутком вектора на числоназивається вектор.

Вектор називається нульовим вектором.

Операції додавання і множення на число на множині задовольняють властивостям:

(А)

Означення 5. Множина всіхn-вимірних числових векторів з введеними на ній операціями додавання векторів і множення вектора на число із поля Р, які задовольняють властивостям (А), називається n-вимірним арифметичним простором над полем Р.

2. Лінійна залежність і незалежність векторів.

Нехай

(1)

довільно вибрана система векторів простору . Візьмемо якісь довільні числаі складемо вектор

(2)

Будь-який вектор такого виду називається лінійною комбінацією векторів, а скаляри- коефіцієнтами цієї лінійної комбінації. Якщоє лінійною комбінацією векторів, то говорять, щолінійно виражається черезабо щорозкладається за векторами.

Будь-який вектор системи (1) є лінійною комбінацією векторів цієї системи:

Нульовий вектор є лінійною комбінацією векторів будь-якої системи, оскільки

З поняттям лінійної комбінації векторів тісно пов‘язане поняття лінійної залежності векторів.

Означення 6. Система векторів

простору називаєтьсялінійно залежною, якщо існують такі числа не всі рівні нулю, що

(3)

Система векторів називається лінійно незалежною, якщо рівність можлива лише при

Поняття лінійно залежна і лінійно незалежна система застосовується лише до систем із скінченого числа векторів.

За означенням (6), система, що складається з одного вектора , лінійно залежна, якщо цей вектор є нульовим, і лінійно незалежна, якщо, то звипливає, що

Система із двох векторів лінійно залежна тоді і тільки тоді, коли вектори пропорційні (один з векторів є лінійною комбінацією другого), тобто

Вектори просторуназиваютьодиничним. Система одиничних векторів лінійно незалежна. Дійсно, складемо рівність (3):

за означенням рівності векторів маємо

Розглянемо деякі важливі властивості систем векторів, пов‘язані з поняттям лінійної залежності:

1. Для того, щоб система векторів(1) була лінійно залежною, необхідно і достатньо щоб принаймні один із векторів цієї системи був лінійною комбінацією інших її векторів.

Необхідність умови. Припустимо, що система (1) лінійно залежна, тобто що вектори цієї системи зв‘язані співвідношенням

,

в якому, наприклад, . Тоді

тобто вектор є лінійною комбінацією векторів.

Достатність умови. Нехай один з векторів системи (1), наприклад, є лінійною комбінацією інших її векторів:

Звідси випливає рівність

в якій і отже, система (1) лінійно залежна.

2. (випливає з властивості 1)

Будь-яка система векторів, яка містить нульовий вектор, лінійно залежна.

Справді, нехай в системі (1) перший вектор нульовий (). Тоді очевидна рівністьпоказує, що векторє лінійною комбінацією інших векторів, тобто що система (1) лінійно залежна.

3. Якщо система векторівлінійно незалежна, а система векторівлінійно залежна, то векторє лінійною комбінацією векторів.

Справді, оскільки система векторів лінійно залежна, то існують числа, які не всі дорівнюють нулю, і такі, що виконується рівність

. (4)

Серед коефіцієнтів саме, оскільки присправджувалася б рівність

,

в якій не всі коефіцієнти дорівнюють нулю і, отже, система векторів була б лінійно залежною. Оскільки, то із співвідношення (4) випливає, що

тобто що є лінійно. Комбінацією векторів.

Множину, що складається з будь-яких k () векторів системи (1) називатимемопідсистемою цієї системи.

4. Якщо деяка підсистема системи векторів (1) лінійно залежна, то й система (1) лінійно залежна.

Нехай лінійно залежною є підсистема . Тоді має місце співвідношення

,

в якому не всі коефіцієнти дорівнюють нулю. Звідси випливає, що

,

і, отже система (1) лінійно залежна.

З твердження (4) випливає, що всяка система векторів містить два рівні або пропорційні вектори, лінійно залежна.

5. Якщо система векторів (1) лінійно незалежна, то і будь-яка її підсистема також лінійно незалежна. (Довести це самостійно).

Розглянемо систему векторів

(5)

або

(6)

в яких координати на діагоналі відмінні від нуля

Системи векторів (5) і (6) називають ступінчастими або трапеційними.

При маємо трикутні системи

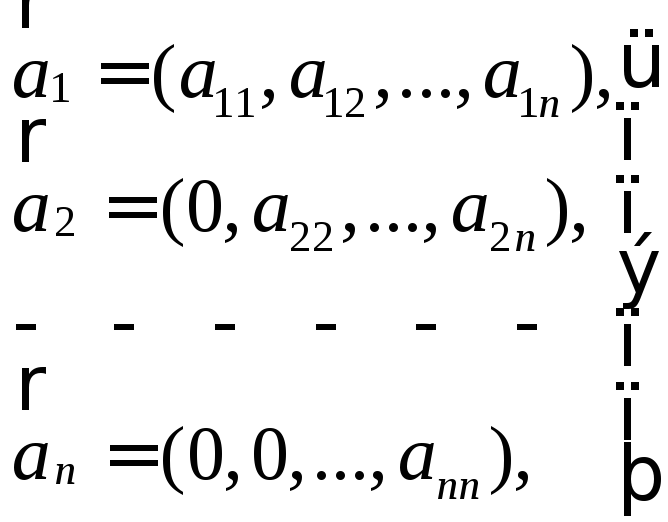
6. Ступінчаста система векторів лінійно незалежна.

Покажемо, що рівність

(7)

можлива лише при умові, що всі числа дорівнюють нулю.

Справді, підставимо (5) в (7)

Звідси маємо

оскільки , то

, то

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

, то

Отже, рівність (7) виконується тільки при , а це означає, що ступінчаста система векторів (5) лінійно незалежна.

Наслідки. 1) Трикутна система векторів лінійно незалежна.

2) Діагональна трикутна система лінійно незалежна

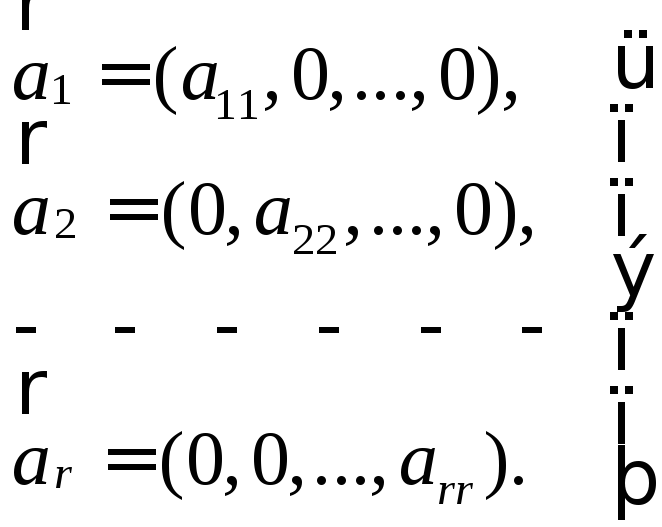
3) В просторі існує лінійно незалежна система, яка мітить рівно n векторів.

Прикладом такої системи є система одиничних векторів , через які лінійно виражається будь-який вектор

Нехай - деякий n-вимірний числовий вектор.

Вектори

іназивають укороченими векторами відносно вектора.

7. Якщо система n-вимірних векторівлінійно залежна, то і система укорочених векторіві

також лінійно залежна.

Розглянемо теореми про лінійну залежність.

Теорема1. Нехай

(8)

і (9)

дві системи векторів простору , причому. Тоді, якщо кожен вектор системи (8) є лінійною комбінацією векторів системи (9), то система (8) лана йно залежна.

За умовою кожен вектор розкладається за векторами:

(10)

Треба показати, що система (8) лінійно залежна, тобто, що існують такі числа не рівні одночасно нулю, для яких справедлива рівність:

(11)

Підставимо (10) в (11):

Звідси отримуємо

Оскільки вектори лінійно незалежні, то ця рівність виконується коли

(12)

(12) – однорідна система лінійних рівнянь, в якій число рівнянь менше числа невідомих Така система завжди має не нульовий розв‘язок.

Отже, числане всі рівні нулю і задовольняють систему (12).

Теорема 2. В просторі будь-яка система, яка складається більше ніж із n векторів, лінійно залежна.

Для доведення достатньо застосувати теорему 1 до двох систем векторів: і, (). Кожний з векторівє лінійною комбінацією одиничних векторів. В силу теореми 1 множинабуде лінійно залежною.

Наслідок. В просторі максимальне число лінійно незалежних векторів дорівнює n.

3. Базис і ранг в системі векторів.

Нехай

- (13)

довільна система векторів простору і

(14)

- деяка лінійно незалежна підсистема цієї системи.

Означення7. Лінійно незалежна підсистема (14) системи векторів (13) називається базисом системи (13), якщо кожний вектор системи (13) є лінійною комбінацією векторів цієї підсистеми.

Приклад. В системі векторів підсистемає базисом, оскільки векторинепропорційні, а тому лінійно незалежні, і векторє лінійною комбінацією векторів цієї підсистеми:

,

Іншим базисом системи є підсистема . Векторлінійно виражається через цю підсистему:

Двома базисами вичерпуються всі базиси даної системи.

Приклад показує, що в системі векторів може бути декілька базисів, але число векторів у кожному базисі одне й те ж.

Теорема3. Два різні базиси однієї і тієї ж системи векторів містять однакову кількість векторів.

Доведення випливає з теореми 1. Дійсно, нехай

- два різних базиси системи S. З двох чисел r і s – одне більше другого. Нехай . До системів цьому випадку можна застосувати теорему 1, з якої випливає, що системалінійно залежна, що протирічить умові. Таким чином,.

Система може співпадати з усім простором. Базисом просторує система ізn лінійно незалежних векторів, через які лінійно виражається будь-який вектор цього простору.

Приклади 1). У просторі (пряма) кожен ненульовий вектор утворює лінійно незалежну систему (базис).

2). У просторі (площина) кожна пара не колінеарних векторів є базисом (три вектори лінійно залежні).