
Приклади. Знайти модуль і аргумент комплексних чисел:
1.
![]()
![]()
![]()
2.
![]()
![]()
![]()
3.
![]()
![]()
![]()
Нехай
![]() Оскільки
Оскільки![]()
![]() (рис. 1), то отримуємо
(рис. 1), то отримуємо
![]() (2)
(2)
Цей запис називають тригонометричною формою комплексного числа. Інакше, поряд із зображенням (2) має місце і таке:
![]() (3)
(3)
Звідси випливає:
рівність двох комплексних чисел, заданих
у тригонометричній формі, означає, що
модулі цих чисел відрізняються на число,
кратне
![]() .
.
Якщо
![]()
![]() та
та![]()
![]()
Приклад.
Записати в тригонометричній формі число
![]()
Маємо
![]()
![]()
Отже, ![]()
або в загальному вигляді тригонометрична форма числа
![]()
Додавати і віднімати комплексні числа, записані в тригонометричній формі, незручно. Однак операції множення і ділення над такими числами виконувати зручно. Нехай дано два числа:
![]()
![]() .
.
Перемножимо ці числа
![]()
![]()
![]()
тобто
![]() (4)
(4)
Співвідношення
(4) є записом комплексного числа
![]() в тригонометричній формі,
в тригонометричній формі,![]() - модулем комплексного числа
- модулем комплексного числа![]() ,
а
,
а![]() - аргументом цього числа.
- аргументом цього числа.
Отже,
![]()
![]() (5)
(5)
Таким чином, модуль добутку комплексних чисел дорівнює добутку співмножників, а аргумент добутку комплексних чисел дорівнює сумі аргументів співмножників.
Ці правила поширюються на будь-яке скінченне число множників
![]()
![]()
Припустимо, що
![]() і поділимо
і поділимо![]() на
на![]() :
:
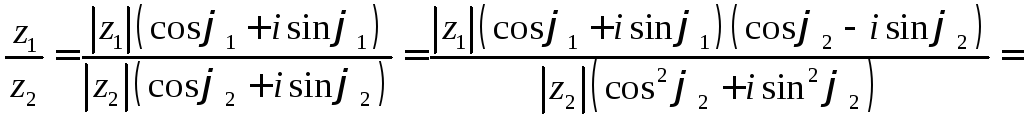
![]()
тобто
![]() (6)
(6)
Звідси знаходимо
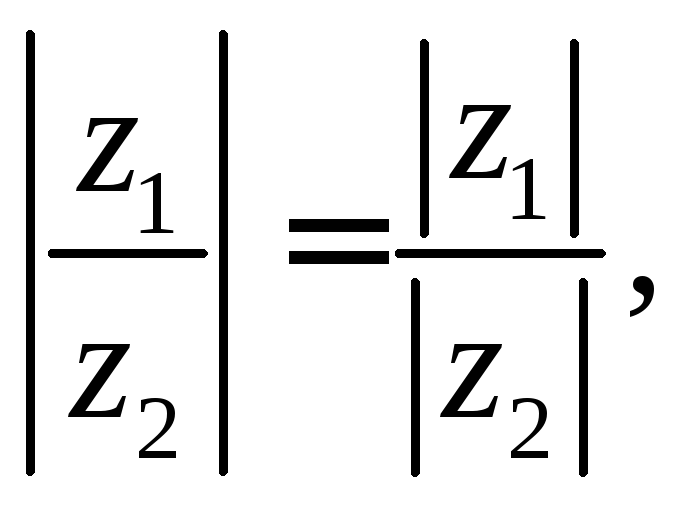
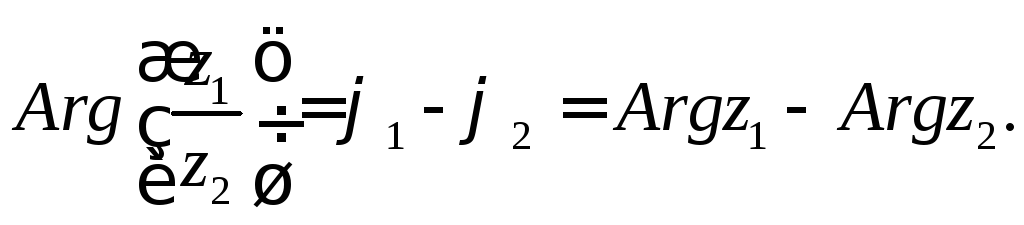
Отже, модуль частки двох комплексних чисел дорівнює модулю діленого, поділеному на модуль дільника; аргумент частки двох комплексних чисел дорівнює різниці аргуменів діленого і дільника.
Дамо геометричне тлумачення операцій над комплексними числами, зображаючи їх точками або напрямленими відрізками площини.
Н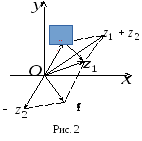 ехай
дано комплексні числа
ехай
дано комплексні числа![]() і
і![]() .
Зобразимо їх на площині векторами (рис
2). Тоді z1+z2
зображується
діагоналлю паралелограма, побудованого
на цих векторах, як на сторонах. Різниця
z1-z2
дорівнює
сумі
z1+(-z2).
Вектор, яким
зображується число -z2,
симетричний вектору числа z2
відносно
початку координат.
.
Зобразимо їх на площині векторами (рис
2). Тоді z1+z2
зображується
діагоналлю паралелограма, побудованого
на цих векторах, як на сторонах. Різниця
z1-z2
дорівнює
сумі
z1+(-z2).
Вектор, яким
зображується число -z2,
симетричний вектору числа z2
відносно
початку координат.
Щоб побудувати вектор, який відповідає різниці досить сполучити кінець вектора числа z2 з кінцем вектора числа z1 і утворений вектор перенести паралельно самому собі, помістивши його початок у точку 0.
Таким чином, додавання і віднімання комплексних чисел в алгебраїчній формі з геометричної точки зору зводиться до додавання і віднімання векторів, якими зображуються ці числа.
Геометричний зміст множення і ділення комплексних чисел з‘ясувати також неважко, використавши запис їх у тригонометричній формі. Справді, нехай дано два комплексних числа
![]() і
і
![]()
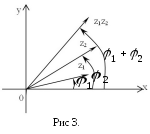
Для побудови
вектора, що зображує добуток
![]() (рис. 3), треба повернути вектор
(рис. 3), треба повернути вектор![]() навколо початку координат на кут
навколо початку координат на кут![]() і потім подовжити його в
і потім подовжити його в![]() раз (при
раз (при![]() це буде не подовження а стиснення).
це буде не подовження а стиснення).
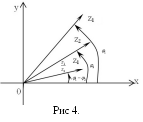
Для побудови
вектора, що зображує частку
![]() (рис. 4), треба вектор
(рис. 4), треба вектор![]() повернути навколо точки 0 на кут
повернути навколо точки 0 на кут![]() (тобто на кут
(тобто на кут![]() за годинниковою стрілкою) і потім
стиснути в
за годинниковою стрілкою) і потім
стиснути в![]() раз (при
раз (при![]() це буде не стиснення, а подовження).
це буде не стиснення, а подовження).
Для модуля суми і модуля різниці справедливе таке твердження: Модуль суми двох комплексних чисел не більший від суми модулів цих чисел, а модуль різниці двох комплексних чисел не менший від абсолютної величини різниці модулів цих чисел.
С правді,
розглянемо суму і різницю чисел z1
і z2
правді,
розглянемо суму і різницю чисел z1
і z2
(рис. 5). На основі відомих співвідношень між сторонами трикутника маємо
![]()
![]() ,
тобто
,
тобто
![]()
![]()
Рівності мають місце лише тоді, коли числа z1 і z2 зображуються векторами, що лежать на одній прямій.
3. Піднесення комплексного числа до цілого степеня.
Якщо комплексне
число задане в алгебраїчній формі, тобто
![]() то
для піднесення його до цілого додатного
степеня треба застосувати формулу
бінома Ньютона і тоді при будь-якому
невід‘ємному цілому
то
для піднесення його до цілого додатного
степеня треба застосувати формулу
бінома Ньютона і тоді при будь-якому
невід‘ємному цілому![]() узяти
узяти
![]()
![]()
![]()
![]()
Якщо комплексне число задане в тригонометричній формі, то піднесення його до цілого степеня виконують за формулою Муавра.
Т еорема.
Для будь-якого цілого числа
еорема.
Для будь-якого цілого числа
![]() справедлива рівність
справедлива рівність
![]() (7)
(7)
яка називається формулою Муавра.
![]() Спочатку методом
математичної індукції доведемо
справедливість формули (7) для натуральних
Спочатку методом
математичної індукції доведемо
справедливість формули (7) для натуральних
![]() .
При
.
При![]() формула (7), очевидно, правильна.
формула (7), очевидно, правильна.
Припустимо, що
вона справедлива для
![]() ,
тобто
,
тобто
![]()
Доведемо, що вона
справедлива і для
![]() ,
тобто
,
тобто
![]()
Дійсно,
![]()
![]()
![]()
Отже, формула (7)
за принципом математичної індукції
справедлива для будь-якого натурального
показника
![]() .
.
Припустимо, що
![]() - ціле від‘ємне число. Вважатимемо, що
- ціле від‘ємне число. Вважатимемо, що![]() (
(![]() - натуральне число). Тоді
- натуральне число). Тоді

![]()
![]()
Отже, і при будь-якому цілому від‘ємному показнику формула (7) справедлива.
При
![]() справедливість формули (7) очевидна.
справедливість формули (7) очевидна.![]()
А. Муавр (1667-1754) – англійський математик (за походженням француз). Формулу названо ім‘ям Муавра тому, що в неявному вигляді вперше вона зустрічається в його працях, починаючи з 1707 р. Сучасного вигляду формулі Муавра надав Леонард Ейлер (1748 р.).
Приклади.
1.
![]()
2.

3.
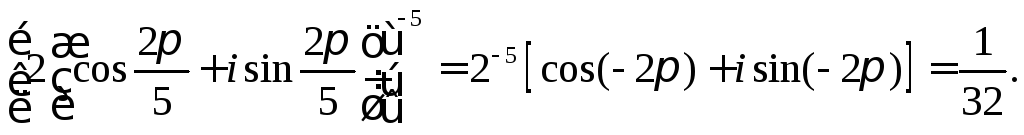
Якщо у формулі
Муавра візьмемо
![]() то дістанемо рівність
то дістанемо рівність
![]() (8)
(8)
Ця рівність дає
змогу виразити
![]() і
і![]() через
через![]() і
і![]() .
Розклавши ліву частину рівності (8) за
формулою бінома Ньютона, матимемо
.
Розклавши ліву частину рівності (8) за
формулою бінома Ньютона, матимемо
![]() (9)
(9)
Прирівнявши окремо
дійсні частини й коефіцієнти уявних
лівої і правої частин рівності (9),
дістанемо записи
![]() і
і![]() через
через![]() і
і![]() .
.
Покажемо це,
наприклад, для
![]() .
.
![]()
звідки
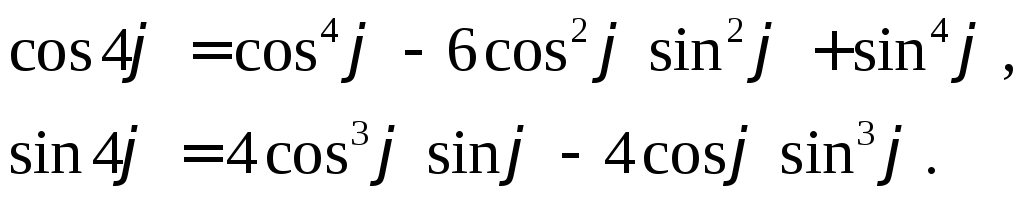
Добування кореня з комплексного числа
Розглянемо питання
про добування квадратного кореня з
комплексного числа. Припустимо, що
квадратний корінь з числа
![]() існує і дорівнює
існує і дорівнює![]() ,
тобто
,
тобто![]()
Тоді
![]() або
або
![]() .
(10)
.
(10)
Визначимо x і y. Для цього прирівняємо дійсні й уявні рівності (10). Дістанемо
![]() (11)
(11)
![]() (12)
(12)
Піднісши обидві
частини кожної з цих рівностей до
квадрата і почленно додавши їх, матимемо
![]() Звідси
Звідси
![]() (13)
(13)
(беремо додатне
значення кореня, оскільки числа x і y
дійсні, і, отже,
![]() ).
).
З рівностей (11) і (13) знаходимо
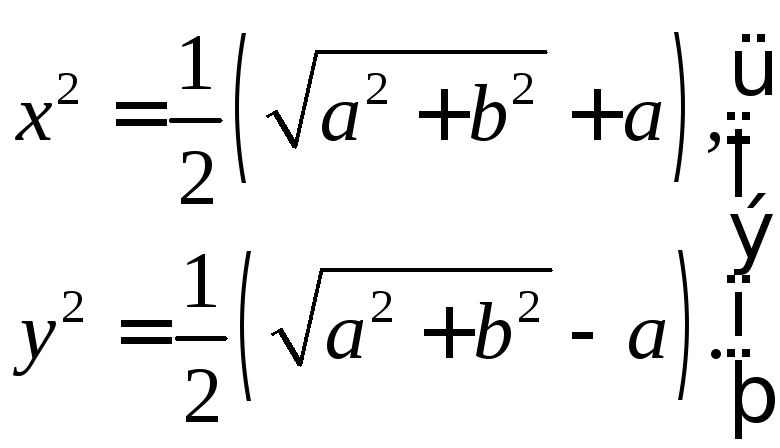 (14)
(14)
Звідси випливає, що
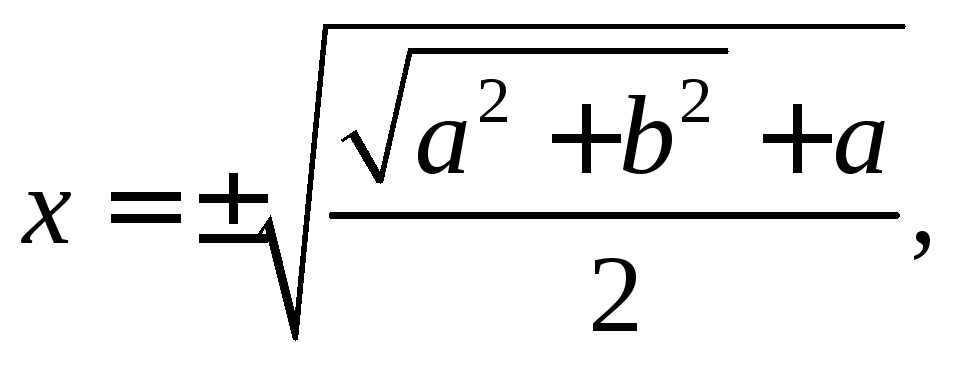
![]()
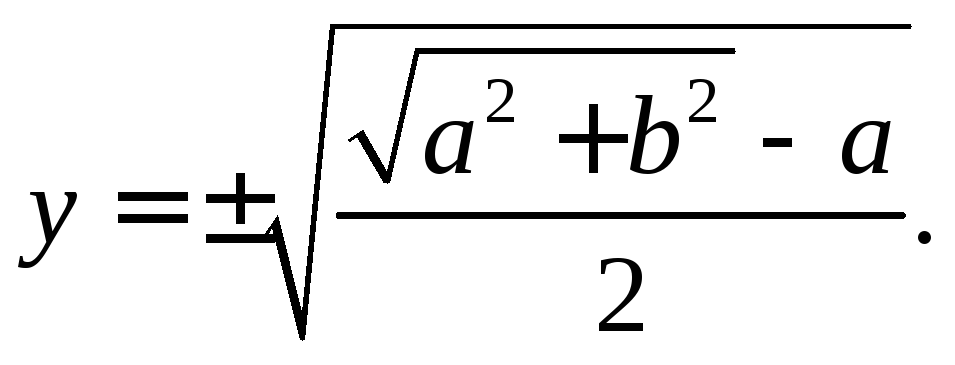 (15)
(15)
За рівність (12) знак добутку xy повинен збігатися із знаком числа b. Отже, при b>0 значення x і y повинні мати однакові знаки і тому радикали треба брати з Тим самим знаком. Якщо b<0, то значення x і y повинні мати протилежні знаки і, отже, радикали треба брати з тригонометричними знаками. Таким чином, маємо формули:
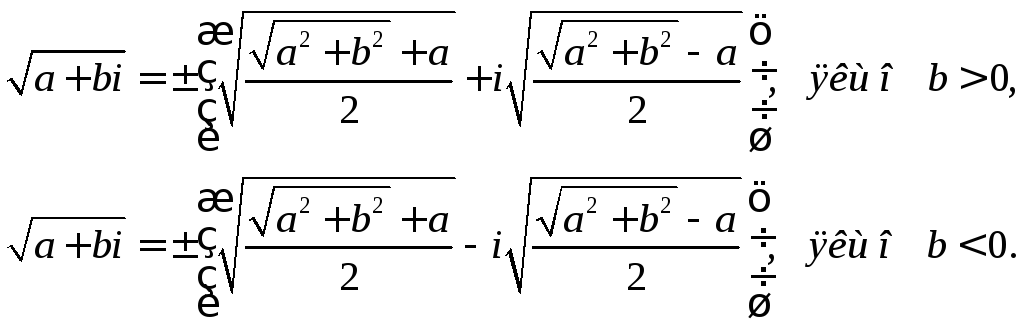 (16)
(16)
Якщо
![]() то
то![]()
Приклади.
1.
![]()
2. Розв‘язати рівняння
![]()
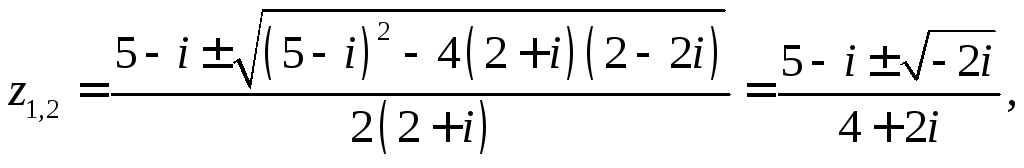
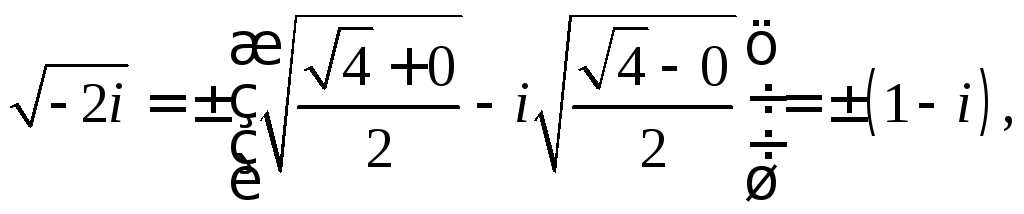
![]()
Д обути
корінь вищого (ніж другий) степеня з
комплексного числа в алгебраїчній формі
в загальному випадку неможливо.
обути
корінь вищого (ніж другий) степеня з
комплексного числа в алгебраїчній формі
в загальному випадку неможливо.
Означення.
Коренем n-го степеня (n-будь-яке натуральне
число) з комплексного числа
![]() називатимемо таке число
називатимемо таке число![]() ,
що
,
що![]() ,
і позначатимемо його символом
,
і позначатимемо його символом![]()
Нехай комплексне
число
![]() задане в тригонометричній формі
задане в тригонометричній формі![]() .
Припустимо, що
.
Припустимо, що![]() ,
,![]() .
Тоді
.
Тоді
![]() .
.
Однак, за формулою Муавра,
![]() .
.
Отже,
![]() .
(17)
.
(17)
Відомо, що два
комплексні числа рівні тоді і тільки
тоді, коли рівні їхні модулі, а аргументи
або рівні, або відрізняютьбся доданком,
кратним
![]() .
Тому з рівності (17) випливає, що
.
Тому з рівності (17) випливає, що![]() ,
,![]() де k- будь-яке ціле число. Звідси
де k- будь-яке ціле число. Звідси![]() ,
,![]() де
де![]() - арифметичне значення кореня з додатного
числа
- арифметичне значення кореня з додатного
числа![]() ,
оскільки
,
оскільки![]() є число додатне.
є число додатне.
Отже,
![]() ,
(18).
,
(18).
![]() -
довільне ціле число.
-
довільне ціле число.
Корінь n-го
степеня з комплексного числа має лише
n різних значень, які знайдемо за формулою
(18) при
![]() Позначимо ці значення символами
Позначимо ці значення символами![]() Тоді
Тоді
![]()
![]() (19)
(19)
Таким чином,
![]() має n значень, які визначаються за
формулою (19).
має n значень, які визначаються за
формулою (19).
З‘ясуємо, який
геометричний зміст мають значення
![]() при
при![]() .
Всі n значень
.
Всі n значень![]() мають той самий модуль
мають той самий модуль![]() .
Аргумент
.
Аргумент![]() дорівнює
дорівнює![]() ,
аргументи
,
аргументи![]() дістаємо послідовним додаванням кута
дістаємо послідовним додаванням кута![]() .
.
Отже, точки
комплексної площини, якими зображують
числа
![]() ,
є вершинами правильного n-кутника,
вписаного в коло радіуса
,
є вершинами правильного n-кутника,
вписаного в коло радіуса![]() з центром у початку координат, причому
одна з вершин зображує число
з центром у початку координат, причому
одна з вершин зображує число![]() з аргументом
з аргументом![]() ,
чим однозначно визначається положення
всіх інших вершин.
,
чим однозначно визначається положення
всіх інших вершин.
Приклад.
1. Знайти
![]() .
.
Запишемо число
![]() в тригонометричній формі
в тригонометричній формі
![]()
Далі, за формулою (19), маємо
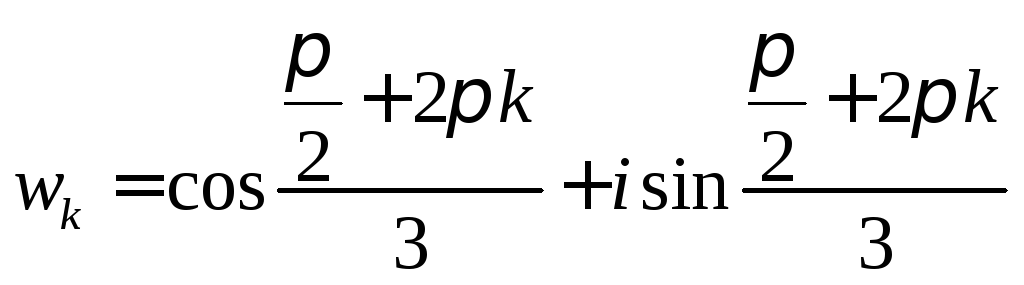 ,
,![]()
З відси
дістанемо
відси
дістанемо

На рис. 6 зображено
значення кореня 3-го степеня з числа
![]() .
.
