§2. Характеристика оптимизирующих переменных.

Эти переменные выбираются из числа входных переменных процесса.

Если в число оптимизирующих переменных включены конструктивные характеристики процесса (размеры, типы конструкций и т.п.), то решается задача оптимального проектирования.

Если в число оптимизирующих переменных не включены конструктивные характеристики процесса (размеры, типы конструкций и т.п.), то решается задача оптимального управления. В этом случае оптимизирующие переменные называются управляющими переменными и поиск их оптимальных значений осуществляется с целью определения наилучших режимных параметров действующих процессов.

Оглавление

§3. Численные методы оптимизации.

Для решения задачи оптимизации численным методом на компьютере необходимо располагать:

• адекватной математической моделью оптимизируемого процесса, реализованной на компьютере;

• подпрограммой расчёта критерия оптимальности;

• программой конкретного метода оптимизации (градиентные методы, симплексный метод и методы случайного поиска);

Обобщённая блок-схема оптимизации численным методом:

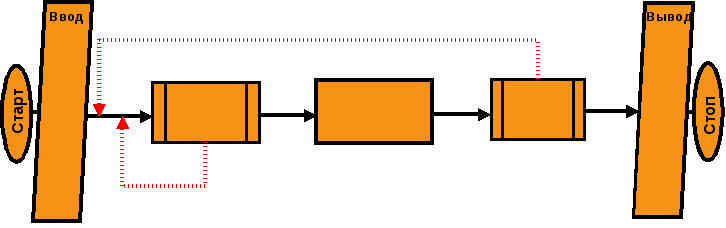
Оглавление

3.1. Экспериментально-статистический метод оптимизации.

Эти методы применяются, когда построить математическую модель невозможно. Известны лишь факторы (оптимизирующие переменные) и выходная переменная y (критерий оптимальности), значение которой определяется опытным путём.

Формулировка задачи оптимизации :

Так как выходная переменная определяется из опытных данных, для поиска её экстремальных значений необходимо реализовать оптимальную стратегию экспериментирования.

Функция критерия оптимальности

в этом случае может быть представлена в виде поверхности отклика, одинаковые значения которой для двух факторов ( x₁, x₂ ) изображаются линиями постоянного уровня ( y = const ). Эти линии являются проекциями сечений поверхности отклика на плоскость факторов. Искомая экстремальная точка поверхности отклика соответствует точке «0».

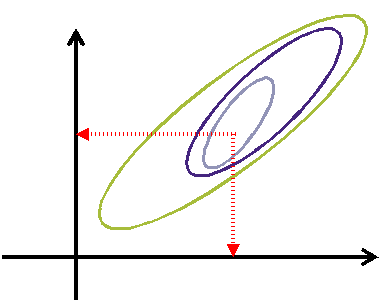
В этом случае используется «шаговый» метод движения по поверхности отклика с целью определения её экстремального значения.

При этом выделяются два этапа планирования эксперимента:

• движение в факторном пространстве к «почти стационарной области»;

• уточнение положения экстремума в «почти стационарной области».

Оглавление

3.2. Движение к экстремуму методом крутого восхождения.

Движение к экстремуму осуществляется по направлению градиента (антиградиента) функции отклика у.

Вектор градиента определяет направление наискорейшего возрастания функции и для

равен:

где

- единичные векторы в направлении осей координат;

- проекции вектора градиента на оси координат

Для m = 2 движение методом крутого восхождения можно представить:

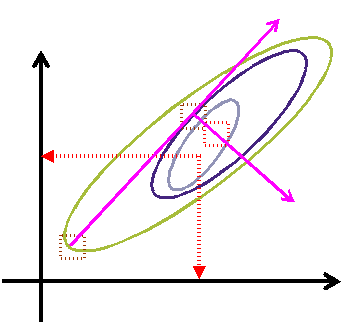
- центры планов эксперимента первого порядка (ПФЭ)

- центр плана эксперимента второго порядка (ОЦКП)

Последовательные координаты поиска экстремума в факторном пространстве определяются по формуле:

, где

h - задаваемый фактор шага по направлению вектора-градиента;

s - номер точки экспериментирования;

- движение к максимуму (+) или к минимуму (-);

Величина y здесь определяется из уравнения регрессии, которое является линейным относительно факторов и коэффициентов:

Это уравнение используется для локального описания поверхности отклика в областях, далёких от её экстремального значения.

Ограниченная область факторного пространства, где справедливо это уравнение регрессии, задаётся центром области – центром плана эксперимента:

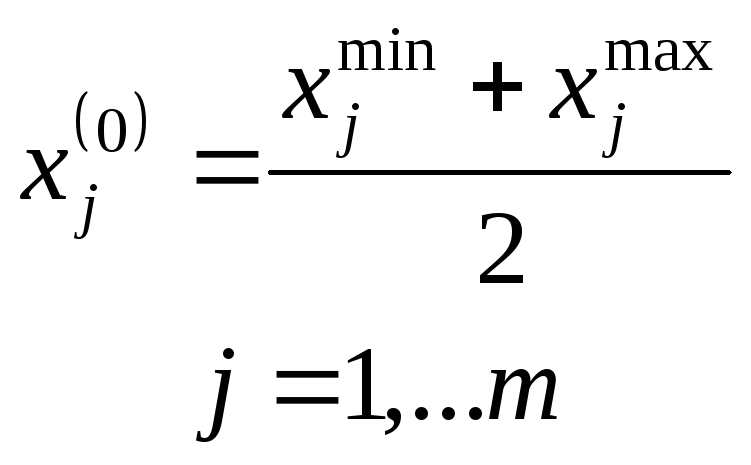
и интервалом (точнее, полуинтервалом) варьирования факторов:

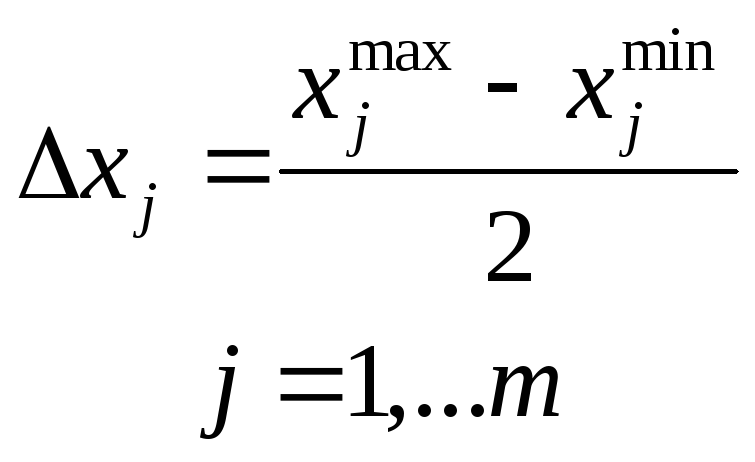
Для локальной области факторного пространства уравнение регрессии записывается с кодированными факторами:

где

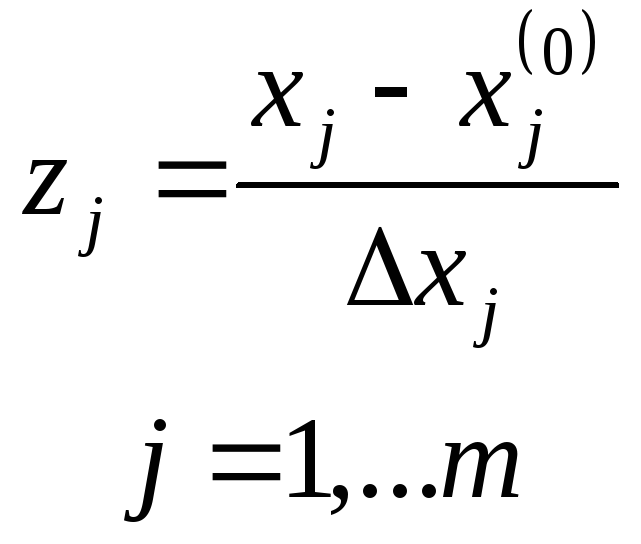
В результате минимальному значению фактора соответствует z_j = -1, максимальному - z_j = 1, а центру плана эксперимента – точка с координатами z_j = 0, j = 1, …m

Коэффициенты уравнения регрессии с кодированными факторами отличаются от коэффициентов уравнения регрессии с натуральными значениями факторов x_j и определяются из полного факторного эксперимента (ПФЭ), проведённого в рассматриваемой ограниченной области.

Одним из таких свойств является свойство ротатабельности, которое характеризует равную предсказательную способность уравнения регрессии с кодированными факторами на одинаковом расстоянии от центра плана.

Для характеристики предсказательной способности уравнения регрессии используется оценка дисперсии выходной переменной , которая из-за статистической независимости коэффициентов и их одинаковой дисперсии в случае ПФЭ определяется по формуле:

где

- одинаковая для всех коэффициентов оценка дисперсии ,

где

n - число опытов ПФЭ

- дисперсия воспроизводимости выходной переменной у , определяемая по параллельным опытам

ρ² - квадрат расстояния из центра плана до рассматриваемой точки факторного пространства:

Величина, обратная , принимается за меру точности уравнения регрессии.

Точность уравнения для убывает пропорционально квадрату радиуса сферы ρ² и одинакова для всех эквидистантных точек.

Поэтому в факторном пространстве нельзя выделить ни одно предпочтительное направление, и вектор градиента ( )не хуже, в смысле предсказания величины выходной переменной у , чем любое другое направление.

Однако вектор-градиент ( ) характеризует направление наискорейшего возрастания функции у и в этом смысле движение по нему является наиболее предпочтительным.

Для определения координат вектора-градиента ( ) используется адекватное уравнение регрессии, полученное по результатам ПФЭ:

Задаётся фактор шага h , и из центра плана ПФЭ (- начальное приближение) выполняется шаг по градиенту в сторону экстремального значения функции отклика, определяются координаты нового центра плана в факторном пространстве - .

Здесь снова проводится ПФЭ, обрабатываются его результаты, вычисляется новое направление вектора-градиента:

по которому выполняется шаг

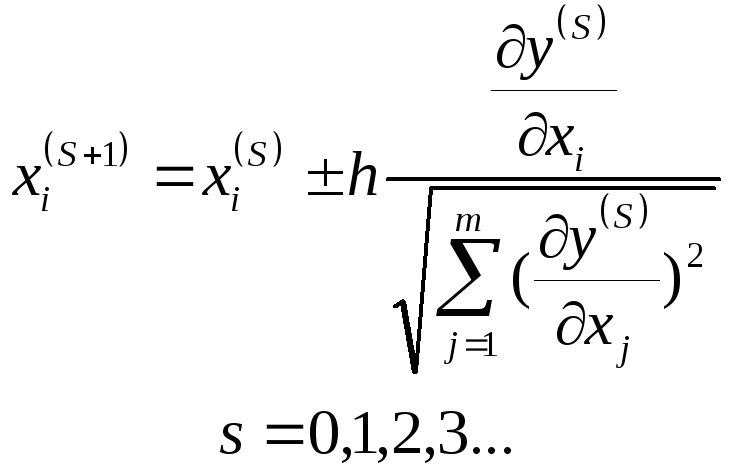
в сторону экстремума. Процедура последовательного экспериментирования продолжается до тех пор, пока не будет достигнута область, близкая к экстремальному значению функции отклика.

Близость почти стационарной области может быть установлена с помощью t – критерия Стьюдента путём оценки значимости различия между экспериментальными и расчётными величинами в центре плана.

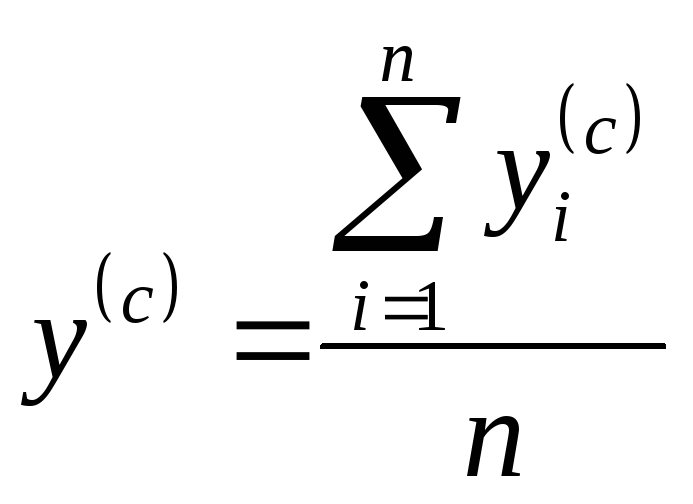
Условие близости экстремума функции отклика имеет вид:

где

f_e = k – 1 - число степеней свободы

k- число параллельных опытов

β - заданная доверительная вероятность (обычно 0,95)

Оглавление