Вернуться к списку лекций

Тема 09. Оптимизация математической модели хтп.

Оглавление

§1. Постановка задачи оптимизации.

§2. Характеристика оптимизирующих переменных.

§3. Численные методы оптимизации.

3.1. Экспериментально-статистический метод оптимизации

3.2. Движение к экстремуму методом крутого восхождения

3.3. Уточнение положения экстремума в почти стационарной области

§4. Блок-схема алгоритма экспериментально-статистического метода оптимизации.

Задания для самопроверки

§1. Постановка задачи оптимизации.

Оптимизация – это процедура нахождения наилучших условий проведения химического процесса.

Задача оптимизации рассматривается как математическая задача поиска экстремального значения функции многих переменных.

Формулировка задачи оптимизации для многих переменных:

Необходимо найти такие значения оптимизирующих переменных (ресурсов оптимизации) из допустимой области их определения , которые обеспечивают экстремальную (наибольшую или наименьшую) величину критерия оптимальности.

В результате задачу оптимизации можно представить в следующим виде:

Связь выходных переменных с другими переменными задаётся отображением с физико-химическим оператором:

где входные переменные , определяющие состояние моделируемого объекта, разбиваются на две группы переменных: - оптимизирующие переменные, которые можно контролировать и регулировать и - контролируемые, но не регулируемые переменные (не могут использоваться как ресурсы оптимизации).

В результате задача оптимизации представляется в следующем виде:

На оптимизирующие переменные и выходные переменные могут накладываться ограничения (возможность изменения переменных только в определённых пределах).

На практике выходные переменные при решении задачи оптимизации определяются либо из экспериментальных данных – экспериментально-статистический метод оптимизации, либо с помощью математических моделей процессов – численный метод оптимизации.

Математические модели в этом случае формализуются с помощью отображения с функциональным оператором:

Замена вектора выходных переменных на вектор оценок выходных переменных , полученных при расчёте по математической, модели позволяет рассматривать задачу оптимизации как математическую задачу поиска экстремума функции многих переменных на компьютере.

Задача: определение максимума функции R = R( u )

Результат решения: .

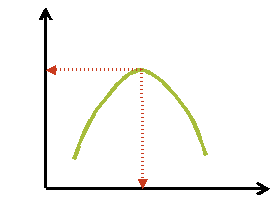
Пример:

Для последовательной реакции A → P → S , изменение концентраций компонентов которой представлено ниже на рисунке, можно сформулировать следующую задачу оптимизации: найти оптимальное время реакции ( t_opt ), при котором концентрация промежуточного продукта Р будет максимальной.

Для решения задачи оптимизации необходимо:

• сформировать критерий оптимальности ( R );

• выбрать оптимизирующие переменные( );

• реализовать конкретный метод определения экстремального значения критерия оптимальности ( численный или экспериментально-статистический ).

Критерий оптимальностиявляется количественной характеристикой качества функционирования процесса.

Различают физико-химические (концентрация целевого продукта, примеси, выход продукта) и экономические (себестоимость, прибыль, рентабельность) критерии оптимальности.

Значение критерия оптимальности зависит от выходной переменной , рассчитываемой с помощью математической модели (численный метод оптимизации). Предполагается, что при оптимизации применяются математические модели, для которых предварительно решена задача идентификации. Соответственно коэффициенты модели не показаны в равенстве:

Если адекватную математическую модель процесса построить не удаётся, то значение выходной переменной в уравнении:

определяется из опытов (экспериментально-статистический метод оптимизации). В этом случае реализуется оптимальная стратегия проведения эксперимента (активный эксперимент).

Требования к критерию оптимальности:

• критерий оптимальности должен быть количественным

• критерий оптимальности должен быть единственным

• критерий оптимальности должен монотонно изменяться в зависимости от оптимизирующих переменных.

Таким образом, при выборе критерия оптимальности необходимо стремиться к тому, чтобы его функция была унимодальной с одним экстремумом и не содержала точек разрыва.

Оглавление