2. Кинематический расчет привода (редуктора)

Передаточное число редуктора (показывает во сколько раз снижается скорость вращения)

=n₁/n₂=2.14 , Округлим это значение до величины, входящей в стандартный ряд, тогда u=2

КПД редуктора привода и подшипника качения:

_ПК =0.995 _s=P₂/P₁= _{зуб пер}*(_{подшиб кач})²=0,98*0,995² =0,97

Тогда =0.97*0.995^2=0.96 ;

Мощность Р1=50/0.96=52.07кВт

Где - коэффициент полезного действия (КПД) привода, равный произведению частных КПД.

Требуемая мощность электродвигателя:

Р₁= P₂/ _s=52.07кВт

Крутящий момент на валах:

Угловая скорость: =(п*n)/30

₁= (π*n₁)/30=750*3.14/30=78.54 с^-1

₂= (π*n₂)/30=36.65с^-1

Вращающий момент: T=P/ W

T₁=P₁/ W₁= 52.08*10^3/78.54=662.92кН*мм

T₂=P₂/ W₂=50*10^3/36.65= 1364.19кН*мм

Валы	Pк Вт	nоб/мин	с-1	Tн*м
I	52.08	750	78.54	663.43
II	50	350	36.65	1366.12

3. Расчет зубчатых колес (зубчатой передачи) редуктора

3.1Выбираем материалы со средними механическими характеристиками:

Для выбора материалов шестерни и колеса можно руководствоваться данными из таблиц, приведенных в справочных материалах.

Рекомендуется назначать для шестерни и колеса сталь одной марки , но обеспечить соответствующей термообработкой твердость поверхности зубьев шестерни на 20-30 едениц Бринеля выше, чем у колеса. В связи с тем, что задание не предусматривает требования в отношении габаритов передачи, выбираем материалы со средними механическими характеристиками:

для шестерни:

сталь – 45, термическая обработка - улучшение, твердость – НВ 230;

для колеса:

сталь – 45, термическая обработка - улучшение, твердость - НВ 200.

3.2Определение межосевого расстояния : Допускаемое контактное напряжение [_H] при расчете зубчатых колес определяется по формуле:

[_H]=

где _{H lim b} - предел контактной выносливости при базовом числе циклов.

Для углеродистых сталей с твердостью поверхностей зубьев менее НВ 350 (=200НВ) и термической обработкой (улучшением)

_{H lim b} = 2НВ + 70=2*200+70=470

[Sh]-допускаемый коэффициент безопасности. При однородной структуре материала ( нормализация, улучшение, объемная закалка) [S_H]=1,10

К_HL – коэффициент долговечности; при числе циклов нагружения больше базового, что имеет место при длительной эксплуатации редуктора (срока службы), принимают К_HL=1.

K hl max ≥ KHL ≥ 1;

Nho – база испытаний. При средней твердости поверхности 200НВ Nho= 10 млн. циклов. Ne- расчетное число циклов нагружения зубьев за весь срок службы передачи.

Ne= 60nL , где n – частота вращения того из колес, по материалу которого определяют допускаемое напряжение, об/ мин. L – срок службы передачи, ч.

[_H]=0,45([_H1]+[ _H2]);

Для колеса [_H2]= ==481,81 МПа

для шестерни [_H1]= ==427,27 МПа

Для повышения надежности расчета в качестве допускаемого контактного напряжения принимаем [_H] того колеса, для которого оно меньше, т.е. тихоходного колеса ( быстроходное колесо в передаче – шестерня).

[]f= Kfc*Kfl , где fo – предел выносливости зубьев при изгибе, соответствующий базе испытаний. При обработке улучшением твердости 200НВ предел выносливости зубьев равен но=1.8НВ=1.8*200=360

[Sf]- допускаемый коэффициент безопастности. Для зубчатых колес, изготовленных из литых заготовок [Sf]= 2.3.

Kfc- коэффициент, учитывающий влияние двустороннего приложения нагрузки. При одностороннем приложении нагрузки Kfc= 1.

Kfl – коэффициент долговечности. При твердости 350НВ

1≤ Kfl ≤ 2.1

Nfo – база испытаний. Для всех сталей Nfo= 4*10^6. Ne определяется так же, как и в случае с [_H] . На практике обычно Ne>Nfo , поэтому принимаем Kfl =1 . Теперь можно определить допускаемое напряжение изгиба:

Расчетное допускаемое контактное напряжение:

= (360/2.3 )*1*1= 156.52 Н/мм^2

[_H]=0,45(481,81 +427,27)=409,08.

[_H] 1,25[_H2] 409,08534,08 условие выполнено.

Коэффициент , примем выше рекомендуемого для этого случая.

=1,25

Для косозубых колес коэффициент ширины венца по межосевому расстоянию ==0.4

b- ширина венци колеса, мм. Aw- межосевое расстояние, мм. Коэффициент ширины венца принимают из ряда стандартных чисел. При симметричном расположении колес относительно опор : Ψа=0.4 -0.5 .

Кна- коэффициент, учитывающий неравномерность распределения нагрузки между зубьями. Для косозубых колес он зависит от окружной скорости. При v= до 10м/с он равен 1.05-1.15 , а Kfa=0.72-0.91.

Коэффициенты неравномерности распределения нагрузки по ширине зубчатого венца при расчете на контактную прочность Кнв и при расчете на изгиб Kfb зависят от упругих деформаций валов, корпусов, самих зубчатых колес, погрешностей изготовления и сборки, износа подшипников. При твердости металла хотя бы одного из колес меньше 350НВ и скорости v≤ 15 м/с принимают Khb=Kfb=1.

Динамический коэффициент Khv также определяют в зависимости от окружной скорости. При v до 10 м/с Khv=1.0-1.1 ( для косозубых колес). Kfv=1.2.

Межосевое расстояние из условия контактной выносливости активных поверхностей зубьев:

=215.63~200 мм( округлим до стандартного табличного значения).

Ближайшее значение межосевого расстояния по ГОСТ 2185-66

=200 мм

3.3 Геометрический расчет:

Нормальный модуль зацепления принимаем = 4.08 ~ 4

Принимаем по ГОСТ 9563-60 =4 мм.

Примем предварительно угол наклона зубьев =10.9 и определим числа зубьев шестерни и колеса:

_{Z1= 35 Ze=104}

Тогда : Z2=Ze-Z1= 69

Основные размеры шестерни и колеса:

диаметры делительные:

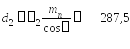
Проверка: мм;

диаметры вершин зубьев:

da1=d1+2mn=151,9 da2=295,66

ширина колеса мм;

ширина шестерни мм;

.

Проверка контактных напряжений

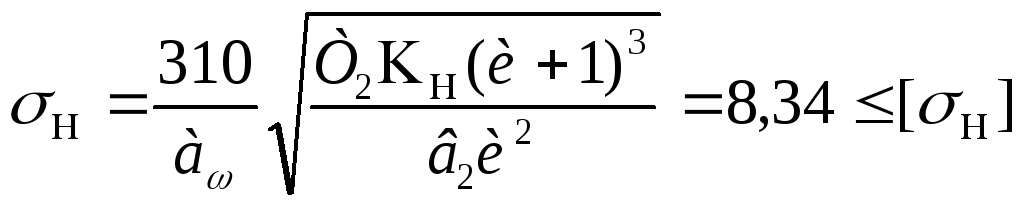что ниже допускаемых Проверяем зубья на выносливость по напряжениям изгиба:

Эквивалентное число зубьев

у шестерни

у колеса

Bmin=arcsin4mn/b=10.9

Проверка прочности зубьев на изгиб: Из-за меньшего числа зубьев зуб шестерни у основания более тонкий, чем у колеса. Этот факт учитывается коэффициентом форму зуба Yf . Рекомендуемые значения Yf в зависимости от эквивалентного числа зубьев zv приведены в таблице:

Z(zv)	17	20	25	30	40	50	60	80	>100
Yf	4.28	4.09	3.90	3.80	3.70	3.66	3.62	3.61	3.60

Суммарное число зубьев для косозубых колес =Zu1+Zu2=104

Эквивалентное число зубьев косозубого колеса рассчитывается по формуле: Zv= (z^2)/cos^2B=73/14 МПа.

P=2T2/mnz2= 9664.81 σf=(3.61* 9664.81/86.3*4)*0.91*1*1.2=108.35

Условие прочности выполняется: