Машина как система. Физический, технологический, расчетный аспекты структурирования.
Машина - устройство для преобразования энергии, материалов и информации с целью облегчения труда человека.
В зависимости от характера рабочего процесса различают:
энергетические машины, преобразующие в механическую энергию иные виды энергии, и наоборот (электродвигатели, паровые двигатели, двигатели внутреннего сгорания, турбины и др.);
технологические машины, которые изменяют размеры, форму, свойства или состояние обрабатываемых предметов и материалов (металлорежущие и деревообрабатывающие станки, роботы и т.д.);
транспортирующие машины, которые преобразуют энергию двигателя в энергию перемещения масс, изделий, объектов труда (конвейеры, подъёмные краны и др.);
информационные машины, предназначенные для получения и преобразования информации (компьютеры и другие машины, выполняющие контрольно-измерительные операции, функции регулирования и управления технологическими процессами).
Деталь– изделие, изготовленное из однородного по наименованию и марке материала без применения сборочных операций.
Звено– группа деталей, образующая подвижную или неподвижную относительно друг друга механическую систему тел.
Сборочная единица – изделие, составные части которого подлежат соединению на предприятии-изготовителе посредством сборочных операций.
Узел– законченная сборочная единица, состоящая из деталей общего функционального назначения и выполняющая определенную функцию в изделиях одного назначения только совместно с другими составными частями изделия (муфты, подшипники качения и др.).
Механизм– система подвижно соединенных деталей, предназначенная для преобразования движения одного или нескольких тел в целесообразные движения других тел (например, кривошипно-ползунный механизм, механические передачи и т. п.).
Аппарат– прибор, техническое устройство, приспособление, обычно некая автономно-функциональная часть более сложной системы.
Агрегат– унифицированный функциональный узел, обладающий полной взаимозаменяемостью.
Привод- устройство, посредством которого осуществляется движение рабочих органов машин. В ТММ применяется адекватный термин – машинный агрегат.
Физическое структурирование механизма. Виды кинематических пар.
Машина- это устройство, создаваемое человеком, для облегчения физического и умственного труда, увеличения производительности путем частичной или полной замены человека.
Машины состоят из механизмов.
Механизм- система тел, предназначенная для преобразования движения одних тел (одного или нескольких) в требуемое движение других.
Например: механизм подачи заготовок, механизм сцепления, механизм торможения и т.д.
Механизмы состоят из звеньев и кинематических пар.
Звено- одно или несколько жестко соединенных твердых тел.
Кинематическая пара- соединение двух звеньев, допускающее относительное движение.
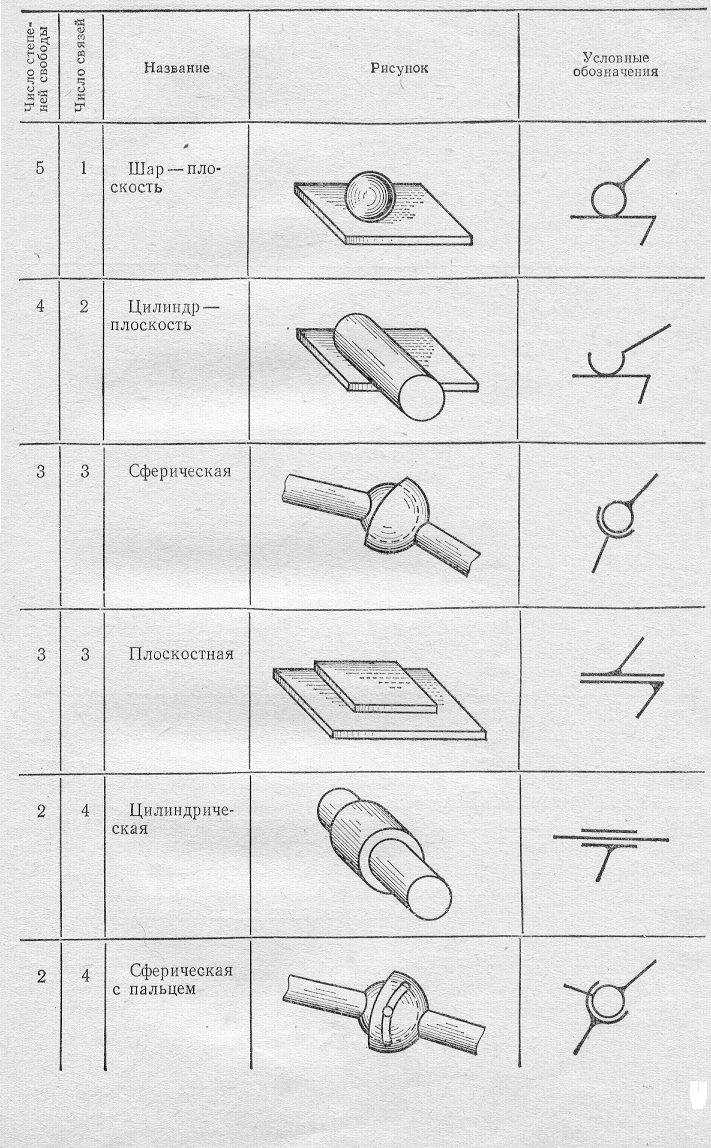
Подвижность механизма по Чебышеву и Сомову - Малышеву. Пассивные связи и лишние степени свободы.
Формула Чебышева: Wпп=3n -2pн -pв,
Где n — число подвижных звеньев механизма, рн — число низших КП, рв — число высших КП.
При выводе этой формулы предполагалось, что все наложенные связи независимы, т.е. ни одна из них не может быть получена как следствие других. В некоторых механизмах это условие не выполняется, т.е. в общее число наложенных связей может войти некоторое число q избыточных (повторных, пассивных) связей, которые дублируют другие связи, не изменяя подвижности механизма, а только обращая его в статически неопределимую систему. В этом случае при использовании формул Сомова-Малышева и Чебышева эти повторные связи надо вычитать из числа наложенных связей:
W = 6n - (5p1 +4p2 + 3p3 + 2p4 + p5 -q)
или
W = 3n - (2p1 + p2 - q), откуда
q = W - 6n + 5p1 + 4p2 + 3p3 + 2p4 + p5
или
q = W -3n +2p1 + p2
Принцип Ассура.
Закон Ассура: Всякий механизм представляет собою совокупность одного или нескольких, двухзвенных (первичных) механизмов и одной или нескольких групп нулевой подвижности.
Структурной группой Ассура(или группой нулевой подвижности) называется кинематическая цепь, образованная только подвижными звеньями механизма, подвижность которой (на плоскости и в пространстве) равна нулю (Wгр = 0).
Конечные звенья групп Ассура, входящие в две кинематические пары, из которых одна имеет свободный элемент звена, называются поводками.
Классомструктурной группы Ассура называется число кинематических пар, входящих в замкнутый контур, образованный внутренними кинематическими парами группы
Порядокгруппы определяется числом внешних элементов кинематических пар, которыми группа присоединяется к имеющемуся механизму: первая группа присоединяется к первичному механизму, каждая последующая – к полученному механизму (при этом нельзя присоединять группы к одному звену).
Запишем структурную формулу механизма в следующем виде
w = 3(n – 1) – 2p5 = 1.
В этой формуле n – число всех звеньев механизма, включая стойку.
Следовательно, в механизме с w = 1 число звеньев n должно быть четным, так как число кинематических пар V класса не может быть дробным.
Степень подвижности группы Ассура
w = 3n – 2p5 = 0,
Так как p5 может быть только целым числом, то n должно быть четным. Как видно из формулы, простейшей кинематической цепью, удовлетворяющей условию структурной группы, является кинематическая цепь с n = 2 и p5 = 3.
Механизм как несвободная система материальных точек. Виды связей.
В общем случае уравнение связи, налагаемой на точку системы, записывается в виде f(x, y, z, x', y', z', t) = 0
В зависимости от вида уравнения связи делятся так:
1) геометрические и кинематические или дифференциальные;
2) стационарные или склерономные и нестационарные или реономные;
3) голономные и неголономные.
К геометрическим относятся связи, в уравнениях которых входят только координаты точки и, может быть, время, например уравнение y = ax2
Кинематическими или дифференциальными называются связи, уравнения которых кроме координат содержат и первые производные от этих координат и, может быть, время. Примером такой связи может быть связь, наложенная на колесо, катящееся без скольжения по неподвижной поверхности.
Связи, в уравнения которых время явно не входит, называются стационарными или склерономными. Рассмотренные выше связи являются стационарными. Если время явно входит в уравнение связи, то такая связь будет нестационарной или реономной. Например, пусть проволока, на которую надета бусинка, движется вправо с постоянной скоростью V (рис. 59, c). Тогда уравнение связи примет вид y = ax2 - Vt. Так как время входит в уравнение явно, то эта связь нестационарная.
Механическая система называется склерономной, если на нее наложены только стационарные связи, в противном случае она называется реономной.
К голономным относятся все геометрические связи, а также те кинематические (дифференциальные) связи, которые путем интегрирования могут быть сведены к геометрическим. Так кинематическая связь, наложенная на колесо, является голономной, так как ее можно проинтегрировать и свести к геометрической
Механическая система называется голономной, если все ее связи голономные, и неголономной, если хотя бы одна из ее связей является неголономной.
Точечное описание рычажных и кулачковых механизмов.
Кинематический анализ механизмов. Задачи и методы.
Целью кинематического анализа является изучение движения звеньев механизма независимо от сил, действующих на них. При этом принимаются допущения: звенья абсолютно жесткие (не деформируются) и в кинематических парах отсутствуют зазоры.
Основная задача анализа состоит в определении кинематических характеристик движения механизма. В нее включаются:
определение положений звеньев механизма и построение траекторий отдельных точек звеньев.
нахождение линейных скоростей точек механизма и угловых скоростей звеньев.
определение линейных ускорений точек механизма и угловых ускорений звеньев.
Задача анализа решается для проверки того, насколько удачно спроектирован механизм, т.е. насколько его кинематические характеристикисоответствуют заданным. Другими словами, под кинематическим анализом механизма понимают аналитический или графический процесс расчета, в результате которого определяются положения каждого из звеньев механизма, перемещения точек звеньев или углы их поворота, линейные скорости и ускорения точек и угловые скорости и ускорения звеньев по заданному закону движения начального (ведущего) звена.
Сопротивление материалов. Задачи. Гипотезы. Метод сечений. Виды Н.Д.С.
Сопротивление материалов — часть механики деформируемого твёрдого тела, которая рассматривает методы инженерных расчётов конструкций на прочность, жесткость и устойчивость при одновременном удовлетворении требований надежности, экономичности и долговечности.
Основная задача сопротивления материалов - разработка методов, позволяющих подбирать надежные и наиболее экономичные размеры поперечных сечений элементов конструкций, а также наиболее целесообразную их форму.
Основные гипотезы:
Гипотеза сплошности и однородности: материал представляет собой однородную сплошную среду; свойства материала во всех точках тела одинаковы и не зависят от размеров тела.
Гипотеза об изотропности материала: физико-механические свойства материала одинаковы по всем направлениям.
Гипотеза об идеальной упругости материала: тело способно восстанавливать свою первоначальную форму и размеры после устранения причин, вызвавших его деформацию.
Гипотеза (допущение) о малости деформаций: деформации в точках тела считаются настолько малыми, что не оказывают существенного влияния на взаимное расположение нагрузок, приложенных к телу.
Допущение о справедливости закона Гука: перемещения точек конструкции в упругой стадии работы материала прямо пропорциональны силам, вызывающим эти перемещения.
Принцип независимости действия сил (принцип суперпозиции): результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательности их приложения.
Гипотеза Бернулли о плоских сечениях: поперечные сечения, плоские и нормальные к оси стержня до приложения к нему нагрузки, остаются плоскими и нормальными к его оси после деформации.
Принцип Сен-Венана: в сечениях, достаточно удалённых от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагружения и определяется только статическим эквивалентом нагрузки.
Суть метода сеченийзаключается в следующем. Если при действии внешних сил тело находится в состоянии равновесия, то любая отсеченная часть тела вместе с приходящимися на нее внешними и внутренними усилиями также находится в равновесии, следовательно, к ней применимы уравнения равновесия.
Рассмотрим тело, имеющее форму бруса (рис. 1.2, а)
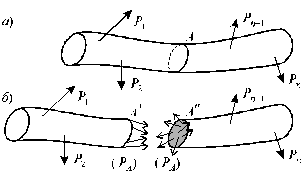
Пусть к нему приложена некоторая система внешних сил Р1, Р2, Р3,..., Рn , удовлетворяющая условиям равновесия, т.е. при действии указанных внешних сил тело находится в состоянии равновесия.
Если рассечь брус сечением А на две части и правую отбросить, то, т.к. связи между частями тела устранены, необходимо действие правой (отброшенной) части на левую заменить некоей системой внутренних сил (PА), действующей в сечении А (рис. 1.2, б).
Обозначая через Pлев и Рправ суммы внешних сил, приложенных соответственно, к левой и правой частям бруса (относительно сечения А), и учитывая, что
Pлев + Рправ = 0 (1.1)
для отсеченных частей бруса получим следующие очевидные соотношения:
Рлев + PA = 0; Рправ - PA = 0. (1.2)
Последние соотношения показывают, что равнодействующая внутренних сил РА в сечении А может определяться с равным успехом из условий равновесия либо левой, либо правой частей рассеченного тела. В этом суть метода сечений.
Основные виды напряжённо-деформированного состояния (НДС)
растяжение-сжатие, сдвиг, кручение, изгиб
9. Растяжение - сжатие. Расчеты n, σ, τ, ε, δl. Диаграмма растяжения.
Растяжение (сжатие) - это вид деформации стержня, при котором происходит изменение его первоначальной длины.
Внутренние силы Nна участках стержня находятся, рассматривая равновесия последовательно отсечённых частей стержня.
σ- нормальное напряжение.σ=(N/S), гдеS– площадь поперечного сечения, части стержня.
ε- относительное удлиние.ε=(ΔL/L).
ΔL- абсолютное удлинение.ΔL=(N*l)/(E*S), гдеE– модуль упругости при растяжении-сжатии.
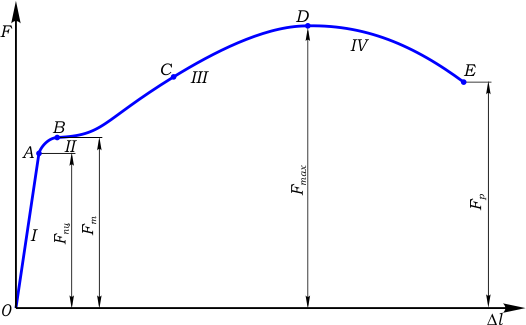
Пример построенной диаграммы растяжения:
F - продольная растягивающая сила, [Н];
Δl - абсолютное удлинение рабочей части образца, [мм]
Вопрос 10)Статически неопределимые балки и рамы – конструкции, в которых уравнений статики недостаточно для определения опорных реакций и внутренних усилий. Число связей, наложенных на статически неопределимую систему,больше того количества связей, которые обеспечивают геометрическую неизменяемость конструкции. Такими связями могут быть как опорные связи, так и стержни самой конструкции. Будем рассматривать балки и простые рамы, то есть такие конструкции, в которых связями, обеспечивающими геометрическую неизменяемость, являются опорные закрепления (опорные связи). Для обеспечения геометрической неизменяемости балки (рамы) в плоскости достаточно трех связей. Каждая связь запрещает какое-то перемещение. Шарнирно-подвижная опора запрещает перемещение по направлению, перпендикулярному плоскости опирания, и является одной связью. Шарнирно-неподвижная опора делает невозможными линейные перемещения по двум взаимно-перпендикулярным направлениям (вертикальному и горизонтальному) и соответствует двум связям, наложенным на конструкцию. Наконец, при наличии жесткого защемления на конце стержня становятся невозможными все перемещения: и вертикальное, и горизонтальное, и угол поворота, поэтому жесткое защемление представляет собой три связи, обеспечивающие геометрическую неизменяемость балки (рамы). Каждая дополнительная связь сверх трех для плоских систем превращает конструкцию в статически неопределимую. Такие дополнительные связи, которые не являются необходимыми для обеспечения геометрической неизменяемости конструкции, называются лишними.
Статически неопределимые системы обладают рядом характерных особенностей:
1. Статически неопределимая система ввиду наличия добавочных лишних связей, по сравнению с соответствующей статически определимой системой оказывается более жесткой.
2. В статически неопределимых системах возникают меньшие внутренние усилия, что определяет их экономичность по сравнению со статически определимыми системами при одинаковых внешних нагрузках.
3. Разрушение лишних связей в нагруженном состоянии, не ведет к разрушению всей системы в целом, так как удаление этих связей приводит к новой геометрически неизменяемой системе, в то время как потеря связи в статически определимой системе приводит к изменяемой системе.
4. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы.
5. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.
6. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.