2012_MATAN-2 / 2012 МАТАН-2 / 2012 ПРАКТИКА / ПРАКТИКА №8 Приложения ОИ в экономике. Несобственные интегралы

2

Практическое занятие:

Тема: Приложения определенного интеграла к решению некоторых задач экономики.

Объём продукции , произведённой за отрезок времени при производительности , равен .

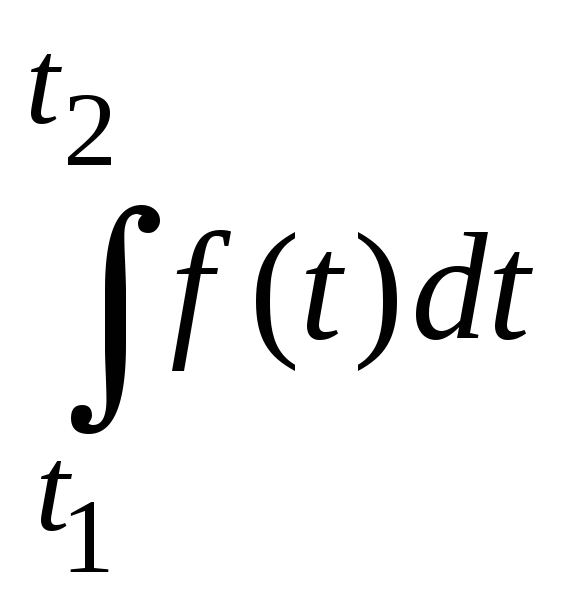Издержки производства при известной функции издержек и заданном изменении объёма производства равны

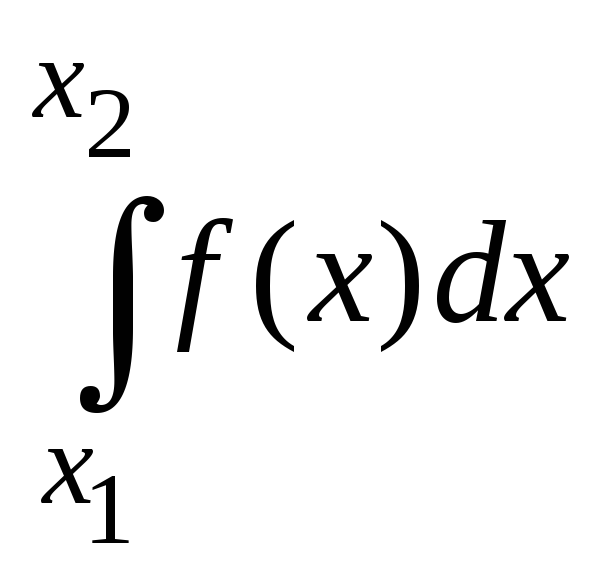
7.277 Найти среднее значение издержек производства некоторой продукции при заданном изменении объёма производства , если функция издержек имеет следующий вид:

а) , ; б) , .

7.278 Доход от инвестиций в некоторое производство равен нулю в течение первого года, а затем изменяется по закону , где - время в годах. Найти среднее значение дохода от инвестиций в течение первых пяти лет.

7.279 Найти среднее значение издержек производства и объём продукции , при котором издержки, задаваемые функцией , принимают среднее значение.

7.280 Определить объём продукции, произведённой рабочим за указанный промежуток времени рабочего дня, если производительность труда характеризуется функцией : а) за пятый час рабочего дня; б) за первые 3 часа рабочего дня.

ОТВЕТЫ:

7.277 а) ; б). 7.278 7.279 , 7.280 а) ; б) .

Тема: Несобственные интегралы.

Интегралы с бесконечными пределами.

Несобственным интегралом первого рода от функции на промежутке называется и обозначается , т.е. . Аналогично: . Если предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.

Несобственный интегралопределяется равенством: , где - произвольное число, причём интеграл в левой части равенства сходится, если сходятся оба интеграла в правой части.

В задачах 7.205-7.213 вычислить несобственные интегралы (или установить их расходимость).

7.205 . 7.206 . 7.207 . 7.208 . 7.209 .

7.210 . 7.211 . 7.212 . 7.213.

Интегралы от неограниченных функций.

Если функция интегрируема при и , то несобственным интегралом второго рода от функции на отрезке называется и обозначается , т.е.. Аналогично, в случае и : . Если предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.

В задачах 7.220-7.228 вычислить несобственные интегралы (или установить их расходимость).

7.220 . 7.221 7.222 . 7.223. 7.224 .

7.225 . 7.226. 7.227 . 7.228 .

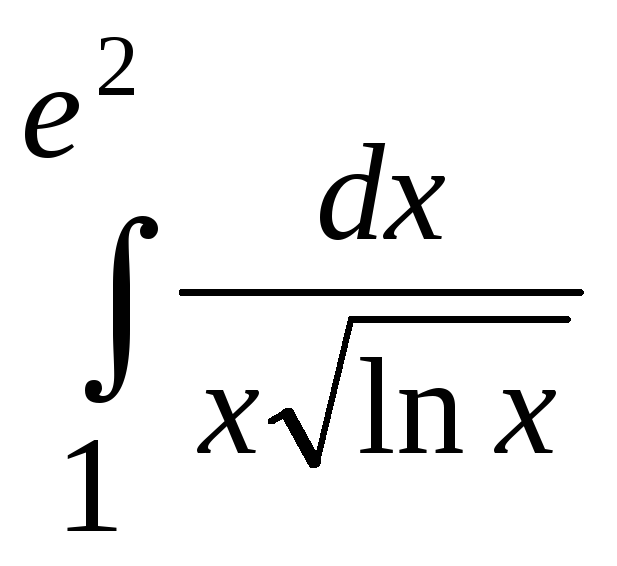ОТВЕТЫ:

7.205 Расходится. 7.206 7.207 7.208 Расходится. 7.209 7.210 7.211 Расходится. 7.212 7.213 7.220 Расходится. 7.221 7.222 7.223 7.224 Расходится. 7.225 7.226 Расходится. 7.227 7.228