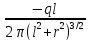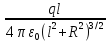If a loop in a basic dc generator suddenly begins rotating at a faster speed, the induced voltage
increases
If an electron moves perpendicular to the uniform magnetic field of magnitude 0.35 T with the speed equal to 4.69×106, what is the radius of its circular orbit? (me = 9.11×10-31kg)
7.63×10-5
Calculate the maximum kinetic energy of protons in a cyclotron of radius 0.50 m in a magnetic field of 0.35 T.
1.46 MeV
A rectangular copper strip 1.5 cm wide and 0.1 cm thick carries a current of 5 A. A 1.2 T magnetic field is applied perpendicular to the strip. Find the Hall voltage that should be produced.
0.442 µV
An ac voltage is applied directly across an 8 µF capacitor. The frequency of the source is 3 kHz, and the voltage amplitude is 30V. Find the voltage across the capacitor in terms of time.
An ac voltage is applied directly across an 8 µF capacitor. The frequency of the source is 3 kHz, and the voltage amplitude is 30V. Find the displacement current between the plates of the capacitor.
A toroidal winding carrying a current of 5 A is wound with 300 turns/m of wire. The core is iron, which has a magnetic permeability of 5000µ0under the given conditions. FindHinside the iron core.
1500
A toroidal winding carrying a current of 5 A is wound with 300 turns/m of wire. The core is iron, which has a magnetic permeability of 5000µ0under the given conditions. FindBinside the iron core.
9.43 T
Assume that a motor having coils with a resistance of 10 Ω is supplied by a voltage of 120 V. When the motor is running at its maximum speed, the back emf is 70V. Find the current in the coils when the motor is first turned on.
12 A
Assume that a motor having coils with a resistance of 10 Ω is supplied by a voltage of 120 V. When the motor is running at its maximum speed, the back emf is 70 V. Find the current in the coils when the motor has reached maximum speed.
5 A
Calculate the inductance of a solenoid containing 300 turns if the length of the solenoid is 25 cm and its cross-sectional area is 4 cm2.
0.181 mH
Calculate the self-induced emf in the solenoid containing 300 turns if the length of the solenoid is 25 cm and the current through it is decreasing at the rate of 50 A/s.
9.05 mV
Calculate the time constant of RL circuit consisting of a 30 mH inductor in series with 6 Ω resistor and 12 V battery.
5 ms
A
block of mass m is accelerated across a rough surface by a force of
magnitude F that is exerted at an angle φ with the horizontal, as
shown above. The frictional force on the block exerted by the
surface has magnitude f. What is the acceleration of the
block?
A
block of mass m is accelerated across a rough surface by a force of
magnitude F that is exerted at an angle φ with the horizontal, as
shown above. The frictional force on the block exerted by the
surface has magnitude f. What is coefficient of friction
between the block and surface
A section of hollow pipe and a solid cylinder have the same radius, mass, and length. They both rotate about their long central axes with the same angular speed. Which object has the higher rotational kinetic energy?
the hollow pipe
Two spheres roll down an incline, starting from rest.Sphere A has the same mass and radius as sphere B, but sphere A is solid while sphereB is hollow. Which arrives at the bottom first?
Sphere A
Two solid spheres roll down an incline, starting from rest. Sphere A has twice the mass and twice the radius of sphere B. Which arrives at the bottom first?
Both arrive at the same time.
When a thin uniform stick of mass M and length L is pivoted about its midpoint, its rotational inertia is ML2/12. When pivoted about a parallel axis through one end, its rotational inertia is:
ML2/3
The three sections of the pipe shown above have areas A1,A2, andA3. The speeds of the fluid passing through each section of the pipe arev1,v2, andv3, respectively. The areas are related byA2= 4A1= 8A3. Assume the fluid flows horizontally. Which of the following is true of the speeds of the fluid in each section in the pipe?
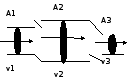
v3 = 2v1
Consider a graphical representation (Fig.) of simple harmonic motion as described mathematically by equation
.
When the particle is at point A on the graph, what can you say about
its position and velocity?
The position is negative, and the velocity is positive
For an object undergoing simple harmonic motion,
the acceleration is greatest when the displacement is greatest
Which of the following statements is not true regarding a mass- spring system that moves with simple harmonic motion in absence of friction?
The potential energy stored in the system is greatest when the mass passes through the equilibrium position.
Consider three point charges located at the corners of a right triangle as shown in Figure, where q1 = q3 = 5.0 μC, q2 =-2.0 μC, and a = 0.10 m. Find the resultant force exerted on q3.
F3=(-1.1i+7.9j)N
An electric dipole is defined as a positive charge q and a negative charge -q separated by a distance 2a. For the dipole shown in Figure, find the electric field E at P due to the dipole, where P is a distance y » a from the origin.
A rod of length l has a uniform positive charge per unit length λ and a total charge Q. Calculate the electric field at a point P that is located along the long axis of the rod and a distance a from one end.
Calculate the ratio of the electrostatic to gravitational interaction forces between two electrons, between two protons. At what value of the specific charge q/m of a particle would these forces become equal (in their absolute values) in the case of interaction of identical particles? (γ=6.67·10-11 m3/(kg·s2), me=9·10-31kg, mp=1·10-27kg, ke=8.99·109 N·m2/ C2)
4·1042 (for electrons); 1·1036 (for proton); q/m=0.86·10-10C/kg
Two positive charges q1and q2are located at the points with radius vectors r1and r2. Find a negative charge q3and a radius vector r3of the points at which it has to be placed for the force acting on each of the three charges to be equal to zero.
A point charge qis located at a distancelfrom an infinite conducting plane. Determine the surface density of charges induced on the plane as a function of separationrfrom the base of the perpendicular drown to the plane from the charge.
A thin infinitely long thread carrying a charge λper unit length is oriented parallel to the infinite conducting plane. The distance between the thread and the plane is equal tol. Find: a) the modulus of the vector of the force acting on a unit length of the thread; b) the distribution of surface charge densityσ(x)over the plane, wherexis the distance from the plane perpendicular to the conducting surface and passing through the thread.
,
A thin wire ring of radius Rcarries a chargeq. Find the magnitude of the electric field strength on the axis of the ring as a function of distancelfrom its centre.
Find the currents I1,I2, andI3 in the circuit shown in Figure.
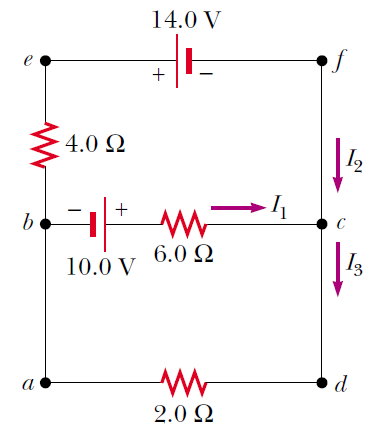
I1=2 A,I2=-3 A,I3=-1 A
The water (H2O) molecule has an electric dipole moment of 6.3·10-30 C·m. A sample contains 1021 water molecules, with the dipole moments all oriented in the direction of an electric field of magnitude 2.5·105 N/C. How much work is required to rotate the dipoles from this orientation (θ=0°) to one in which all the moments are perpendicular to the field (θ=90°)?
1.6·10-3 J
Inside the wall of a house, an L-shaped section of hot-water pipe consists of a straight horizontal piece 28.0 cm long, an elbow, and a straight vertical piece 134 cm long (Figure). A stud and a second-story floorboard hold stationary the ends of this section of copper pipe. Find the magnitude of the displacement of the pipe elbow when the water flow is turned on, raising the temperature of the pipe from 18.0°C to 46.5°C.
0.663 mm
At 25.0 m below the surface of the sea (ρ= 1 025 kg/m3), where the temperature is 5.00°C, a diver exhales an air bubble having a volume of 1.00 cm3. If the surface temperature of the sea is 20.0°C, what is the volume of the bubble just before it breaks the surface? (P0= 1.013* 105 Pa).
3.67 cm3
An aluminum cup of mass 200 g contains 800 g of water in thermal equilibrium at 80.0°C. The combination of cup and water is cooled uniformly so that the temperature decreases by 1.50°C per minute. At what rate is energy being removed by heat? Express your answer in watts. (Specific heat of aluminium and water cal =900 J/kg . °C, cw =4186 J/kg . °C).
88.2 W
A sample of ideal gas is expanded to twice its original volume of 1.00 m3 in a quasi-static process for which P= αV2, α=5.00 atm/m6, as shown in Figure. How much work is done on the expanding gas? (1 atm= 1.013* 105 Pa).
- 1.18 MJ
A sample of an ideal gas is in a vertical cylinder fitted with a piston. As 5.79 kJ of energy is transferred to the gas by heat to raise its temperature, the weight on the piston is adjusted so that the state of the gas changes from point A to point B along the semicircle shown in Figure. Find the change in internal energy of the gas.
3.6 kJ
A multicylinder gasoline engine in an airplane, operating at 2 500 rev/min, takes in energy 7.89 * 103 J and exhausts 4.58 *103 J for each revolution of the crankshaft. How many liters of fuel does it consume in 1.00 h of operation if the heat of combustion is 4.03 * 107 J/L?
29.4 l/h
Suppose a heat engine is connected to two energy reservoirs, one a pool of molten aluminum (660°C) and the other a block of solid mercury (-38.9°C). The engine runs by freezing 1.00 g of aluminum and melting 15.0 g of mercury during each cycle. The heat of fusion of aluminum is 3.97 * 105 J/kg; the heat of fusion of mercury is 1.18* 104 J/kg. What is the efficiency of this engine?
55.4 %
A plane loop of wire consisting of a single turn of cross-sectional area 100 cm2 is perpendicular to a magnetic field that increases uniformly in magnitude from 0.5 T to 2.5 T in a time of 1.5 s. What is the resulting induced current if the coil has a total resistance of 4 Ω?
3A
A 20-turn circular coil of radius 5 cm and resistance 0.5 Ω is placed in a magnetic field directed perpendicular to the plane of the coil. The magnitude of the magnetic field varies in time according to the expression B = 0.02t + 0.05t2, where t is in s and B is in T. Calculate the induced emf in the coil at t = 6 s.
97.4 mV