Цілком інтегровані рівняння Пфаффа в r3

Нехай n = З, а форма ω задовольняє умову (16). Покажемо, що через кожну точку х₀ = (х₀₁, х₀₂, х₀₃) D можна провести інтегральну поверхню рівняння (1), і притому лише одну. Спосіб побудови цієї поверхні нагадує конструкцію розв'язку задачі Коші для рівняння з частинними похідними й передбачає такі кроки.

• Знаходимо інтегральну криву Г : х = ξ(s), s I рівняння Пфаф­фа, яка проходить через точку х₀.

• Задаємо в D векторне поле g(x) С¹ (D → R³ ) так, щоб воно було ортогональне до векторного поля а(х), тобто задовольняло умову

a(x)g(x) = 0, (25)

і не дотикалося кривої Г у жодній її точці. Зокрема, якщо для кожного s 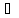I вектори ξ'(s) і rot a(ξ(s)) неколінеарні, то можна покласти

g(x) = rot a(x).

Поле g(х) бажано вибирати так, щоб система

= g(х) (26)

була інтегровною.

• 3 кожної точки кривої Г випускаємо фазову криву системи (26) і таким чином утворюємо поверхню M_Г, яка проходить через цю криву (рис. 2, а).

Виявляється, м_г і є шуканою інтегральною поверхнею рівняння Пфаффа. Точніше, якщо позначити через χ(t, s) розв'язок системи (26), який задовольняє початкову умову χ(0, s) = ξ(s), то для деякого δ > 0 рівняння

^{x = χ (t, s), t ∈ (-δ, δ), s ∈ (s0 – δ, s0 + δ) (27)}

визначають (локальну) інтегральну поверхню рівняння Пфаффа (1), яка проходить через точку х₀.

Множина (27) справді є поверхнею. Цей факт випливає з мірку­вань, наведених у доведенні теореми існування розв'язку задачі Коші для квазілінійного рівняння з частинними похідними першого поряд­ку. Отже, для обґрунтування сформульованого алгоритму залишається переконатися в тому, що

Для цього виведемо диференціальні рівняння, які описують зміну в часі t коефіцієнтів при ds і dt форми . Маємо

(28)

З (25) знаходимо

Тому

З (28) тепер дістаємо

Оскільки виконуються умови (16) та (25), то векторне поле колінеарне векторному полю а. Тому знайдеться така функція ρ(х), що

Це й є шукане рівняння для . Розв'язавши його, дістанемо

Оскільки Г є інтегральною кривою рівняння Пфаффа, то

а тому й . Таким чином, рівняння (27) справді визначають інтегральну поверхню рівняння (1).

Доведемо її єдиність. Нехай, навпаки, існують дві інтегральні поверхні S₁, та S₂ рівняння (1), які проходять через точку х₀ і не збігаються в будь-якому о колі цієї точки. Вони мають спільну дотичну площину П, Ортогональну до вектора а(х₀). Уведемо в R³ нову декартову прямокутну систему координат (х, у, z) із початком О у точці х₀ так, щоб площина хОу збігалася з П, а вісь Оz була спрямована вздовж вектора a(x₀). Тоді кожна поверхня S₁ (i= 1, 2) в околі точки О буде графіком деякої неперервно диференційовної функції z = f_i (х, у). Згідно з припущенням для як завгодно малого е > 0 існує точка (х_е, у_е) така, що |х_е| + |у_е| < е і f₁(х_е, у_е) ≠ f₂(х_е, у_е). Покладемо f= у_еx - х_еy. Рівняння f= 0 визначає площину, яка проходить через точки (х_е, у_е, f₁(х_е, у_е)) і перетинає поверхні S₁ та S₂ по двох різних кривих Г₁ та Г₂.

Повернемося до старих координат. Кожна з кривих Г₁ та Г₂ проходить через точку x₀ і є інтегральною кривою системи (17). Для останньої існує лише одна інтегральна крива, яка проходить через точку x₀. Ця суперечність доводить єдиність інтегральної по­верхні, яка проходить через задану точку.

Приклад 4

Розглянемо рівняння

(2yz + Зх) dx + xz dy + ху dz = 0. (29)

Уданому випадку а(х, у, z) = (2yz + 3х, xz, ху). Оскільки rot а(х, у, z) = (0, у, -z), то умова (16) виконується.

Знайдемо інтегральні криві рівняння (29), які лежать у пло­щині

F y=1.

На ній рівняння (29) набирає вигляду

(2z + 3х) dх + х dz = 0.

Це лінійне відносно z рівняння легко інтегрується, і ми дістаємо сім'ю інтегральних кривих рівняння (29), які лежать у площині y=1:

₍₃₀₎

Тепер побудуємо векторне поле g так, щоб воно не лежало в пло­щині у = 1, задовольняло умову аg = 0 і систему = g(х) можна було легко зінтегрувати. Зручно покласти g(x, у, z) rot а(х, у, z) = (0, у, -z). Відповідна система в симетричній формі має вигляд

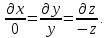
Її загальний інтеграл

yz = c₁, х = с₂. (31)

Тепер для того щоб утворити поверхню з інтегральних кривих сім'ї (31), які для фіксованого с виходять із точок кривої (30), робимо так само, як і під час розв'язування задачі Коші для рівняння з частинни­ми похідними: підставляємо (30) у (31), виключаємо змінну х, в одер­жаному співвідношенні , заміняємос₁, с₂ лівими частинами рівностей (31). Остаточно дістаємо рівняння сім'ї інтегральних по­верхонь рівняння (29):

х²уz + x³ = с.

Звідси, зокрема, випливає, що інтегрувальним множником форми (2yz + Зх) dx + xz dy + ху dz є функція µ = х.

Задача 1

Знайти поверхню, що задовольняє рівняння Пфаффа: (x–y) dx + z dz – x dz = 0.

Розв’язок:

Оскільки (F• rot F) = z – 2x + y і функція z = 2x – y не є розв’язком даного рівняння, то воно не може бути про інтегровано одним співвідношенням. Про інтегруємо його двома співвідношеннями, беручи, наприклад, z = x + y. Тоді отримаємо рівняння

dx – dy = 0,

звідси

y = x + C₁.

Таким чином, одно параметричне сімейство прямих

x = t, y = t + C₁, z = 2t + C₁

задовольняє дане рівняння.

Задача 2

Знайти поверхню, що задовольняє рівняння Пфаффа: 3yz dx + 2xz dy + xy dz = 0.

Розв’язок:

F = (3yz, 2xz, xy).

Так як

rot F = –ix + 2jk – kz та (F• rot F) = 0,

то дане рівняння інтегрується одним співвідношенням. Таким чином, існує множник µ = µ(x, y, z) такий, що rot µF = 0, тобто поле µF потенційне. Звідси, для множника µ маємо рівняння:

або

Інтегруючи перше рівняння, отримуємо загальний розв’язок:

µ = yφ(x,ξ), ξ = yz².

Підставляючи отримане значення µ у друге рівняння, маємо:

звідки знаходимо

φ = x²ψ(x³y²z⁴).

А тоді

µ = yx²ψ(η), η = x³y²z⁴.

Залишається знайти ψ. Для цього скористаємося третім рівнянням. маємо

-9x⁵y³z⁴ ψ'(η) = 0,

звідси

ψ(η) = C.

Таким чином

µ= yx²

(нехай С рівне одиниці). Помноживши почленно дане рівняння на yx², отримуємо рівняння

3x²y²zdx + 2x³yzdy + x³y²dz = 0,

ліва частина якого є повний диференціал функції , яку ми знайдемо вичисливши криволінійний інтеграл

Таким чином,

x³y²z = C

є шуканий інтеграл даного рівняння.

Задача 3

Знайти поверхню, що задовольняє рівняння Пфаффа: (z + xy) dx – (z + y²) dy + y dz = 0.

Розв’язок:

Так як (F• rot F) = z + x – y² ≠ 0, то дане рівняння не може бути проінтегроване одним співвідношенням. Значить, залишається перевірити, чи буде функція z = y² – xy розв’язком цього рівняння. Вичисливши dz = 2ydy – xdy – ydx й підставивши значення z і dz в рівняння, отримаємо тотожність. Отже, поверхня

z = y² – xy

є єдиною, яка ортогональна полю F = (z + xy, -z, -z – y², y).