Інтегральні криві рівняння Пфаффа

Для рівняння (1) завжди можна побудувати одновимірні «інтег­ральні поверхні», тобто інтегральні криві. При n = З це можна зробити таким чином. Візьмемо довільну точку х₀ D. У деякому її околі B(х₀) завжди можна визначити двічі неперервно диференційовну функцію F: В(х₀) → R, для якої grad F(x) був би неколінеарний вектору а(х). Тоді система

(17)

визначає поле напрямів у B(х₀). Це поле напрямів можна задати дея­кою системою в симетричній формі

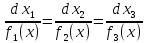, (18)

якій відповідає автономна система

= f(х). (19)

Векторне поле f = (f₁, f₂, f₃) з точністю до множника визначається умо­вою: вектор f(x) ортогональний до векторів а(x) та grad F(x). Наприк­лад, можна покласти

f(x) := | а(x), grad F(х) |, (20)

де | ∙, ∙ | — операція векторного добутку в R³.

Інтегральні криві системи (18) [фазові криві системи (19)] будуть інтегральними кривими системи (17), а отже, рівняння (1).

Зауважимо, що система (17) має очевидний перший інтеграл F. Тому її вимірність можна знизити на одиницю.

Припустимо, наприклад, що а₃(х₀) ≠ 0. Нехай F = F (х₁, х₂) — довільна двічі неперервно диференційовна в околі точки (х₀₁, х₀₂) функція, яка в цьому околі задовольняє умову невиродженості і F(х₀₁,х₀₂)=0. На площині х₁Ох₂ рівняння

F (х₁, х₂) = 0. (21)

визначає криву γ, яка проходить через точку (х₀₁, х₀₂). У просторі R³ воно визначає циліндричну поверхню S із напрямною γ і твірними, паралельними осі Ох₃. Зрозуміло, що вектори а(х) та gгad F(х) неколінеарні в деякому околі точки х₀. Тоді існує єдина інтегральна крива

Г : х = ξ(s), s I (22)

системи (17), яка лежить на поверхні S і проходить через точку х₀.

Для відшукання цієї кривої потрібно рівняння (21) розв'язати відносно однієї зі змінних і результат підставити в рівняння (1). Дістанемо рівняння Пфаффа на площині. Якщо, наприклад, із (21) можна виразити змінну х₂ через х₁, так що х₂ = φ(х₁) (х₀₂ = φ (х₀₁)), то рівняння на площині х₁Ох₃ матиме вигляд

.

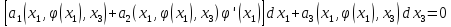Звичайно, функцію F слід намагатися вибирати так, щоб це рівнян­ня легко розв'язувалося. Знайшовши його інтегральну криву х₁ = ξ₁(s), х₃ = ξ₃(s), яка проходить через точку (х₀₁, х₀₂), дістанемо рівняння кривої (22), в якому ξ(s)= (ξ₁(s),φ(ξ₁(s)), ξ₁(s)). Вона водночас є фазовою кривою автономної системи (19), де f(x) визначено фор­мулою (20).

Приклад 3

Приріст dW теплової енергії газу пов'язаний із приростами об'єму dV та тиску dp співвідношенням (закон збереження енергії)

, (23)

де R — газова стала, С_ѵ — теплоємність газу при сталому об'ємі, С_р = С_ѵ+АR — теплоємність газу при сталому тиску, А — стала (термічний еквівалент роботи).

Для даного випадку умова теореми Фробеніуса не виконується:

.

Тому рівняння (23) не є цілком інтегрованим. Із фізичного погляду не означає, що теплова енергія газу не є функцією його стану, який визна­чається значеннями V, р. Тепло, котре поглинається (виділяється) під час деякого процесу — переходу зі стану (V₀, р₀) у стан (V, р), залежить від кривої γ, що сполучає точки x₀ та x, і зображується криволінійним інтегралом

Наприклад, крива, вздовж якої виконується рівність

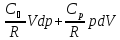, (24)

забезпечує адіабатичний процес (W = const). Із рівняння (24) після відокремлення змінних дістаємо формулу Пуассона для адіабати: , де С — довільна стала.

Якщо скористатися формулою Клапейрона рV = RТ, де Т — абсолютна температура газу, й домножити обидві частини рівнян­ня (23) на 1/T, то побачимо, що

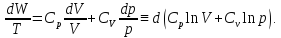
Тому криволінійний інтеграл 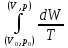не залежить від шляху інтегрування, який сполучає точку (V₀, р₀) зі змінною точкою (V, р). Цей інтеграл визначає ентропію — фізичну величину, яка вже є функцією стану газу.