Цілком інтегровані рівняння Пфаффа

Означення 1

Рівняння (1) називають цілком інтегрованим, якщо через кож­ну точку області D проходить інтегральна гіперповерхня (тобто (п - 1)-вимірна інтегральна поверхня) поля Р.

Як нам уже відомо, при n = 2 кожне рівняння Пфаффа є цілком інтегрованим. Цього, однак, уже не можна стверджувати при n ≥ 3.

Найпростішим прикладом цілком інтегрованого рівняння Пфаффа є рівняння в повних диференціалах, яке характеризується тим, що форма ω є точною, тобто існує функція U(х) С² (D → R) така, що

ω = dU (10)

[Зрозуміло, що точній формі ω відповідає потенціальне векторне поле а(х) = gгad U(х).] У цьому випадку область D розшаровується інтег­ральними гіперповерхнями

M_c :={x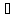 D : U(x) = с} (11)

— поверхнями рівня функції U(х) (стала с пробігає область значень функції U(х)).

Навпаки, припустимо, що для довільної точки х₀ 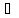D у деякому її околі В(х₀) існує функція U(х) C²(D → R) з ненульовим градієн­том, поверхні рівня якої є інтегральними для поля Р, а отже, орто­гональними до векторного поля а. Легко бачити, що тоді вектори grad U(x) та а(х) будуть колінеарними кожному х D. А це, своєю чергою, означає, що в околі точки х₀ для форми ω існує інтегрувальний множник, тобто функція µ : D → R \ {0}, яка має властивість

µω = dU. (12)

Із невиродженості форми ω випливає, що функція µ неперервно дифе-ренційовна.

Зрозуміло, що рівняння Пфаффа, для якого існує інтегрувальний множник, цілком інтегроване, причому, знаючи інтегрувальний множ­ник, ми зможемо виписати й рівняння інтегральних поверхонь (при­наймні локально).

Далі, якщо для форми

^µω ^{:= b(х) dx ≡ b1(х) dx1 + ... + bn(x) dxn}

виконується рівність (12), то з урахуванням рівностей ,

i, j = 1, …, n дістаємо умови на коефіцієнти b_i :

, i, j = 1, ..., n. (13)

Означення 1

Форму b(x) dx, для якої умови (13) виконуються в кожній точці х D, називають замкненою формою в області D.

Відомо, що в разі виконання умов (13) криволінійний інтеграл ,принаймні в околі точки х₀, не залежить від конкретного вибору шляху γ(х₀, х), який сполучає х₀ з х і цілком лежить в околі точки х₀. Даний інтеграл і визначає функ­цію U(х), яка рівностями (11) задає інтегральні поверхні рівняння (1). Таку функцію назвемо інтегралом рівняння Пфаффа.

Знайдемо необхідні умови існування інтегрувального множника. При b_і = µа_i як наслідок (13) маємо

За допомогою визначників цю рівність можна подати у вигляді

(14)

Оскільки всі мінори третього порядку матриці

дорівнюють нулю, то з огляду на рівності (14) таку саму властивість має й символічна матриця

(15)

Щоб переконатися в цьому, достатньо розкласти будь-які два відповід­них мінори таких матриць за їх першими рядками.

Виявляється, знайдена умова є не лише необхідною, а й достатньою.

Теорема (Фробеніуса)

Для того щоб рівняння (1) було цілком інтегрованим, необ­хідно й достатньо, щоб усі мінори третього порядку матриці (15) перетворювалися в нуль в області D.

Доведення цієї теореми для n = 3 буде наведено в п. 6.2.3. У цьому випадку умова теореми Фробеніуса набирає вигляду

a(x) rot a(x) = 0 (16)

і означає, що векторне поле а(х) ортогональне до свою ротора.