Таблиця 5.1

Значення коефіцієнта

		1,0	2,0	4,0	6,0	10,0
	30,0	31,5	33,3	34,6	34,8	35,1	35,5

Біля опор в балці діють перерізуючі сили, близькі до максимальних, та невеликі згинаючі моменти. Впливом незначних нормальних напружень в цьому випадку нехтують і стійкість стінки перевіряють шляхом порівняння діючих середніх дотичних напружень  в стінці та критичних дотичних напружень _cr:

. (5.27)

Значення середніх дотичних напружень  обчислюють за формулою:

, (5.28)

де

- середнє значення перерізуючої сили в межах відсіку;

та - відповідно висота і товщина стінки.

Місце, де визначається середнє значення в межах відсіку приймають за правилами як для середнього значення.

Значення визначається за формулою:

, (5.29)

тут

- розрахунковий опір сталі зрізу;

- відношення більшого розміру відсіку до меншого.

У формулі (5.29):

, (5.30)

де

- розмір меншого боку відсіку (або).

Якщо одночасно діють нормальні та дотичні напруження, перевірку місцевої стійкості стінки балок симетричного перерізу, підкріплених тільки поперечними ребрами жорсткості, при відсутності місцевого напруження , належить виконувати за формулою:

, (5.31)

де

- слід приймати за [1, табл.6*].

Якщо мають місце місцеві (локальні) напруження , перевірку місцевої стійкості стінки належить виконувати за формулою:

(5.32)

Місцеві нормальні напруження, що входять до (5.32), обчислюють за формулою:

, (5.33)

де

- ділянка стінки, на якій діють локальні нормальні на

пруження в поперечному до осі балки напрямі ;

- розрахункове значення місцевого зосередженого

навантаження.

Рис. 5.9. До визначення локальних напружень:

- межа розповсюдження місцевих (локальних)

напружень

У формулі (5.32) значення івизначають відповідно до[1, п.7.6* і табл.24, 25].

За вимогою [1, п.7.2*], якщо в межах відсіку абозмінюють знак (плюс на мінус або навпаки), їх середні значення слід обчислювати на ділянці відсіку з одним знаком.

В усіх випадках належить обчислюватиза дійсними розмірами відсіку.

5.3.2. Приклад розрахунку місцевої стійкості стінки

В головних балках стінку бажано підкріпити поперечними ребрами жорсткості в місцях опирання балок настилу, щоб запобігти появі місцевих напружень. Але, якщо , то ребра жорсткості в цих місцяхможна не ставити. При цьому обов’язково необхідно додатково перевірити міцність поличок на їх відгинання зосередженими силами, або законструювати їх місцеве підсилення.

У будь-якому випадку крок поперечних ребер балок не повинен перевищувати абов залежності від значення

Оскільки умовна гнучкість стінки у нашому прикладі за формулою (5.21) становить:

,

то стінку балки необхідно підкріпити основними поперечними ребрами жорсткості з максимальним кроком . При цьому, поздовжні ребра жорсткості не потрібні, бо.

З конструктивних міркувань крок поперечних ребер жорсткості вздовж стінки приймаємо , тобто розміщуємо їх не під кожною балкою настилу, а через одну (рис. 5.10).

Місцеві напруження в стінці від опорної реакції балки настилу, що не має під собою поперечних ребер, обчислюємо за формулою (5.33):

,

тут

- опорна реакція балки настилу;

- товщина стінки головної балки;

,

b - ширина полиці балки настилу (рис. 4.4);

- товщина полиці головної балки.

Рис. 5.10. До перевірки місцевої стійкості стійки: - схема розміщення

ребер жорсткості; б - епюра згинаючих моментів і

перерізуючих сил.

Якщо та, необхідна перевірка місцевої стійкості в усіх відсіках стінки. В навчальному прикладі обмежимось перевіркою стійкості лише у відсіку, де змінюється переріз та одночасно діютьі. Цедругий відсік від опори (рис. 5.9).

Оскільки відсік має розміри , то середні значенняіслід обчислити для більш напруженої ділянки довжиною. У нашому випадку перевірку місцевої стійкості за формулою (5.32) належить виконати у двох перерізах:

1-1, на відстані від опори, де прикладена зосереджена сила і;

2-2, на відстані від другого поперечного ребра, де(середина більш напруженої розрахункової ділянки відсіку стінки між поперечними ребрами). Відстань перерізу 2-2 від опори становить(рис. 5.10).

В перерізі 1-1 розрахункові зусилля визначаємо за формулами (5.17) та (5.18):

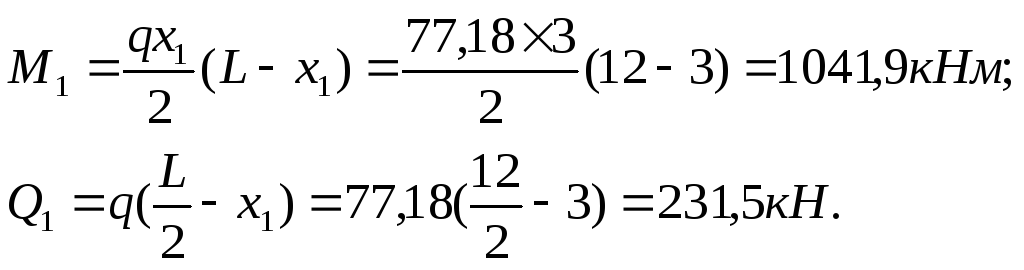
Нормальні стискаючі напруження в стінці на рівні її з’єднання із стиснутим поясом обчислюємо за формулою (5.24):

.

Середні дотичні напруження - за формулою (5.28):

.

Знаходимо і коефіцієнтза формулою (5.26):

.

За [1, табл.24], якщо і, граничне значеннястановить 0,618. В нашому випадку.

Згідно з вказівками [1, п.7.6*, в], якщо і, критичні нормальні напруження обчислюємо за[1, формула (75)]:

,

тут =31,5 - визначаємо за табл.5.1 в залежності від.

Місцеві нормальні критичні напруження за [1, формула (80), та п.7.6*,в]:

,

де

;

- коефіцієнт, який приймається за [1, табл.23] в залежності від

і значення .

Якщо і, маємо

і

.

Критичні дотичні напруження знаходимо за формулою (5.29):

.

Тут, якщо більший бік відcіку і менший:

;

.

Якщо розмір меншого боку відсіку , то за формулою (5.30):

.

Тепер перевіряємо місцеву стійкість стінки другого від опори відсіку в перерізі 1-1 за формулою (5.32):

.

Місцева стійкість стінки в перерізі 1-1 забезпечена.

В перерізі 2-2 цього відсіку розрахункові зусилля також визначаємо за формулами (5.17) та (5.18):

Нормальні стискаючі і середні дотичні напруження:

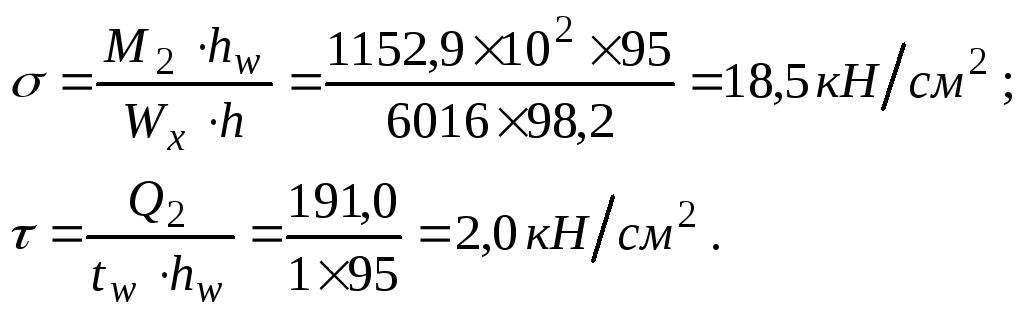
Локальні напруження .

Критичні нормальні та дотичні напруження такі ж, як і в перерізі 1-1 цього відсіку:

; .

Перевіряємо місцеву стійкість стінки в перерізі 2-2 за формулою (5.31):

.

Місцева стійкість стінки другого від опори відсіку забезпечена.

Стійкість стінки в інших відсіках перевіряють аналогічно.

На підставі аналізу результатів обчислень за формулами: (5.32), коли , та (5.31), коли, можна зробити висновок, що наявність локальних напружень збільшує результат розрахунку більш ніж на 30%. І цей вплив зростає із збільшенням зосередженого навантаження.

Тому, якщо за результатами обчислень буде встановлено, що стійкість стінки у відсіку не забезпечена, треба зменшити крок поперечних ребер, або встановити їх в місцях дії зосереджених навантажень, щоб .

Найбільш технологічним типом шарнірного сполучення балок є поверхове, коли балка настилу опирається на верхній пояс головної балки. Якщо опорна реакція балки настилу перевищує 10кН, то для недопущення можливого відгину поясу головної балки передбачають в цьому місті поперечне ребро жорсткості [2, п.3.5], або виконують додаткову перевірку міцності поясу балки на можливий його місцевий відгин. Також виконують місцеве підсилення верхнього поясу в місці опирання балки настилу.

В зварних двотаврових балках, які відносяться до конструкцій груп 2...4 за [1, табл.50*], ребра жорсткості проектуються однобічними з листів з розташуванням їх з одного боку балки [1, п.13.28]. Для однобічних ребер ширина такого ребра має бути не менша ніж

.

Якщо застосовують парні симетрично розташовані ребра, ширина кожного ребра повинна бути

.

Товщина ребра в обох випадках становить

.

Балки перекриття віднесено до конструкцій 2-ї групи, для яких ширина однобічного ребра має бути не менша

.

Це трохи перебільшує ширину звісу поясу в зміненому перерізі балки

.

Тому приймаємо двобічні ребра шириною не менше

.

Остаточно проектуємо .

Товщина поперечного ребра

.

Остаточно приймаємо поперечне ребро з листа – 80х6.

Ребра прикріплюють до стінки двобічними зварними швами .

У прикладі, що розглядається, опорна реакція балки настилу, тобто зосереджене навантаження на головну балку, становить . Виконуючи рекомендації [1, п.7.10] і [2, п.3.5], остаточно проектуємо двобічні поперечні ребра жорсткості в місцях зосереджених навантажень, тобто розташовуємо їх по довжині балки з кроком. Місцеву стійкість стінки, при цьому, не перевіряємо, тому що привона була забезпечена.

З’єднання поясів із стінкою

Розглянемо два варіанти з’єднання поясів із стінкою.

Варіант1, коли крок ребер жорсткості становить . З’єднуємо пояс із стінкою двобічними кутовими швами.

Значення на опорі,відкореговане з урахуванням власної ваги балки):

.

Статичний момент поясу за формулою:

Момент інерції зменшеного перерізу, обчислений у розділі 5, дорівнює

.

Зсуваючі зусилля в першому відсіку визначають відповідно до рис.5.12.

В перерізі 1-1 діє тільки , в перерізі 2-2 діють спільноіF. Очевидно, що в перерізі 2-2 зусилля будуть найбільшими і він буде розрахунковим.

Зсуваючі зусилля за формулою:

;

вертикальне зусилля від дії локальних напружень:

.

Рівнодіюче значення зсуваючого зусилля:

.

Відповідно до норм проектування [1] зварювання виконуємо дротом Св-80А з

, для сталі С245 за [1, табл.51*] маємо ; тоді;і- для ручного напівавтоматичного зварювання відповідно до[1, табл.34*]. Оскільки виконується умова

,

розрахунки проводимо лише за металом шва. Необхідна висота катета шва буде:

.

Відповідно до 1, табл..38^* приймаємо мінімальний катет шва .

Варіант 2, коли крок ребер жорсткості становить .

В цьому випадку можливо прийняти однобічні шви. Зсуваюче зусилля при :-див. вище. Тут, бо дійсна епюраQ є ступінчатою (рис.5.1).

Катет шва за формулою:

.

Відповідно до 1, табл..38^* мінімальний катет шва приймаємо.

Опорна частина балки

Для центральної передачі опорної реакції балки на колону, торцьове опорне ребро (рис.5.6), суміщають з віссю колони, яка проходить через центр ваги останньої. Виступаюча під нижнім поясом частина ребра “а” запобігає позацентровому навантаженню колони в разі прогинання балки. Для щільного прилягання ребра до верху колони торець ребра стругається стругом або фрезою. За цієї умови, а також відповідно до п.7.12 1 за умови

,

опорне ребро розраховують на зім’яття торцьової поверхні (рис.5.6), переріз

1-1):

, (5.1)

де

- ширина і товщина опорного ребра;

- розрахунковий опір сталі зім’яттю.

Рис. 5.6. Опорна частина балки: 1 - торцеве опорне ребро

На практиці ширину опорного ребра звичайно приймають таку саму, як ширина полиці, а товщину опорного ребразнаходять. Ширину ребра не слід приймати меншою ніж 180мм.

Якщо , то розрахунок ребра ведуть за міцністюна стиск і замість в формулу (5.1) підставляють.

Ділянка балки над опорою має перевірятися на стійкість із площини стінки (відносно осі стінки “Y-Y”, рис.5.6), як умовний центрально-стиснутий стержень, на дію опорної реакції V за формулою:

, (5.2)

де

- коефіцієнт поздовжнього згину; як функція гнучкості .

У розрахунковий поперечний переріз цього стержня включають опорне ребро і ділянку стінки балки, що не перебільшує (рис.5.6, переріз 2-2); тоді площа цього перерізу буде:

(5.3)

Розрахункова довжина умовного стержня дорівнює висоті стінки балки. Переріз умовного стиснутого стержня розглядається як неокаймований тавр, поясом якого є опорне ребро. Тоді за[1, табл.29*] місцева стійкість ребра буде забезпечена, якщо відношення ширини його звісу до товщинине перебільшує значень, що визначають за формулою:

, (5.4)

де

- умовна гнучкість умовного стержня відносно осі стінки “Y-Y”,

.

Таким чином умовна гнучкість визначається за формулою:

.

Відповідно, абсолютне значення гнучкості відносно осі Y-Y може бути визначено за формулою:

.

Кутові шви, що прикріплюють опорне ребро до стінки, працюють на зріз від дії опорної реакції. Розрахункова довжина кутових швів не повинна перевищувати [1, п.12.8], а тому мінімально можливий катет шва знаходять із умови міцності зварного шва

(5.5)

при за формулою:

, (5.6)

де

- кількість кутових швів.

Значення берутьне менше, ніж за 1, табл..38^*.

Перевіряють виконання умови . Якщо ця умова не виконується (), то знаходять необхідний катет шва із умови міцності (5.5):

. (5.7)

Опорна реакція балки:

Матеріал - сталь С245 з розрахунковим опором ; розрахунковий опір сталі зім’яттю

Приймаємо ширину ребра , тоді, використовуючи формулу (5.1) знаходимо потрібну товщину ребра із умови зім’яття торцьової поверхні:

.

Конструктивно з урахуванням сортаменту приймаємо товщину ребра . Розмір виступаючої частини ребра приймаємо.

Перевіряємо опорну частину на стійкість із площини балки (із площини стінки) як умовний центрально-стиснутий стержень таврового перерізу з площею, яку обчислюємо за формулою (5.3):

.

Гнучкість стержня:

.

Тут:

- товщина стінки балки;

- висота стінки балки.

За додатком 3 при знайдемо.

Перевіряємо стійкість умовної стійки за формулою (5.2):

.

Стійкість опорної частини балки як умовного центрального стисненого стержня забезпечена.

Умовна гнучкість цього стержня відносно осі “Y-Y”:

.

Граничне значення звісу ребра до його товщини за формулою (5.4):

.

У нашому випадку:

-

- місцева стійкість ребра забезпечена.

Опорне ребро прикріплюється до стінки двобічними кутовими швами. Матеріал для зварювання беремо, як і для поясних швів.

Мінімальний катет шва за формулою (5.6):

.

За додатком 1 приймаємо .

Перевіряємо вимогу . Умова виконується і остаточно приймаємо. Конструктивно цими швами варимо по всій висоті з’єднання опорного ребра із стінкою.