КиОСТСсВС,ОУиО / КиОСТС (для ИИТ) / Лекции / Инженерная психология / Лекция 13

6

Тема 2.8 Алгоритм деятельности оператора

Для описания структуры деятельности оператора в инженерной психологии применяется ряд методов, одним из которых и наиболее распространенным является метод алгоритмического описания деятельности (работы) оператора.

В качестве составляющих алгоритма используются оперативные единицы двух видов: /Pict 13-01/

– элементарные операторы (А) – действия: нажатие кнопки, поворот переключателя, включение тумблера и т.п.;

– логические условия (Р) – образ, понятие, суждение (имеют два исхода): индикатор загорелся или погас, стрелка отклонилась или не отклонилась и т.п.

Для компактной записи алгоритма работы оператора могут использоваться сокращенные обозначения элементарных операторов, логических условий и компонентов панели управления (рис. 13.1) и (рис. 13.2). /Pict 13-2/ и /Pict 13-3/

Рис. 13.1 Обозначения элементарных операторов и логических условий

Рис 13.2 Обозначения компонентов панели управления

Д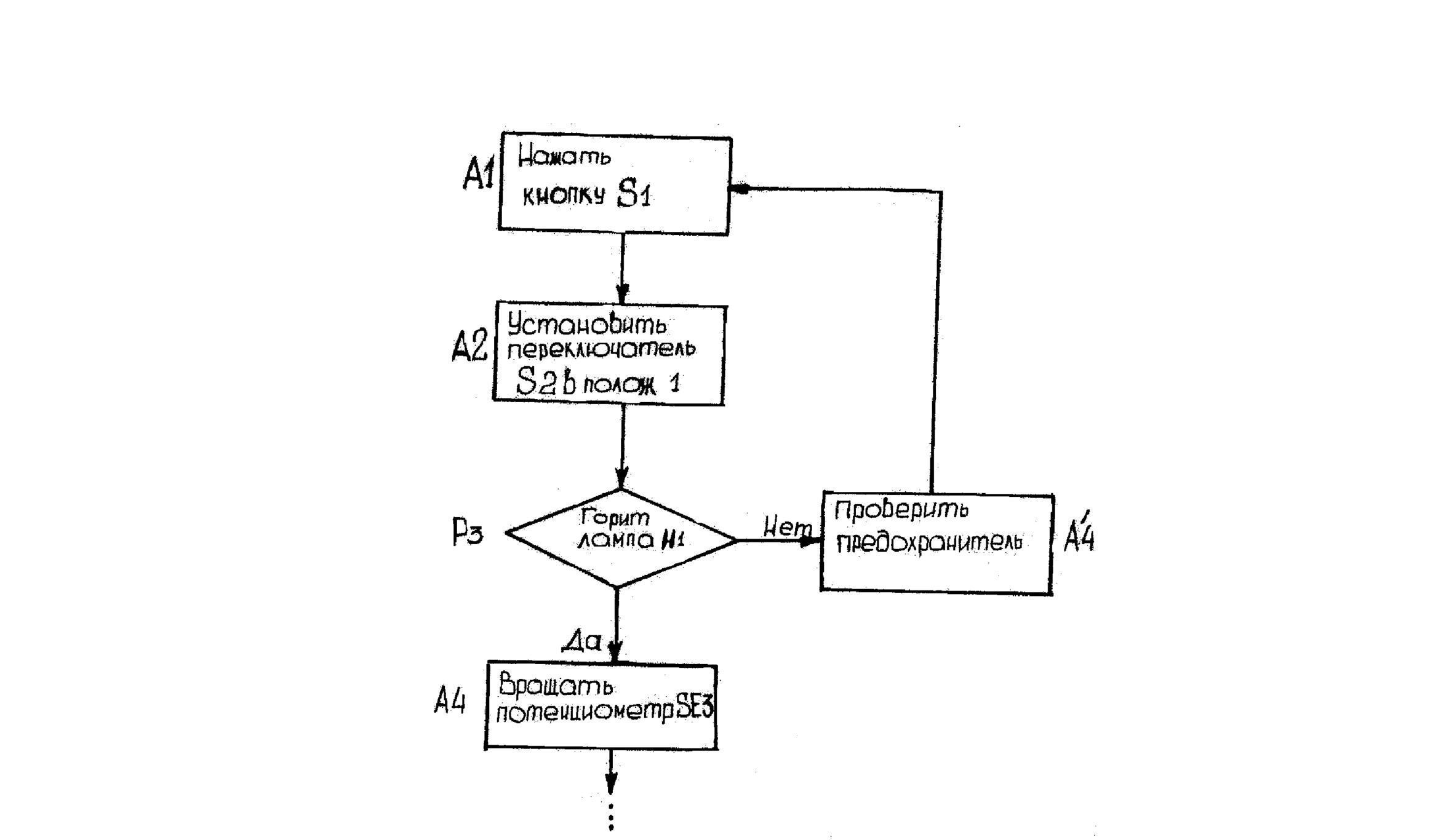ля записи алгоритма применяется структурная схема алгоритма (рис. 13.3). /Pict 13-04/

Рис. 13.3 Структурная схема алгоритма работы оператора с панелью управления

В качестве характеристик алгоритма работы оператора используются нормированные коэффициенты стереотипности и логической сложности.

Пусть алгоритм состоит из N составляющих (N₀ – элементарных операторов и N_л – логических условий), /Pict 13-05/ распределённых соответственно по n0 и nл группам. /Pict 13-06/ Разобъем алгоритм на комплексные группы, включающие в себя по одной группе элементарных операторов и логических условий. Пусть каждая комплексная группа содержит m составляющих алгоритма, из них m0 – элементарных операторов и mл – логических условий. /Pict 13-07/

Стереотипность алгоритма зависит от:

– числа элементарных операторов в алгоритме N0 (чем больше N0 при постоянном Nл, тем больше выражен стереотипный компонент);

– числа групп элементарных операторов n0 ( при постоянных N и N0 с уменьшением n0 увеличивается стереотипность алгоритма);

– общего числа составляющих алгоритма N ( при постоянных N0 и n0 с ростом N уменьшается стереотипность алгоритма);

– распределения операторов по комплексным группам.

Эти факторы учитываются следующими относительными величинами:

– отношением , /Pict 13-08/ характеризующим долю элементарных операторов в алгоритме;

– отношениями и , /Pict 13-09/ характеризующими распределение элементарных операторов по группам.

Тогда выражение для нормированного коэффициента стереотипности можно записать в виде суммы произведений этих отношений: /Pict 13-10/

.

Аналогичным образом можно записать выражение и для нормированного коэффициента логической сложности: /Pict 13-11/

.

Разбивка алгоритма на комплексные группы при вычислении Zн производится, начиная с первой группы элементарных операторов, а при вычислении Lн – с первой группы логических условий, то есть предшествующая ей группа элементарных операторов не учитывается. Поэтому в выражении для Lн вместо N записано N*.

Значения Zн и Lн должны лежать в пределах: /Pict 13-12/

.

Если Zн и Lн лежат в заданных пределах, то в алгоритме достаточно полно учтены возможности человека. При Zн > 0,85 функции оператора целесообразно передать ЭВМ.

Рассмотрим расчет нормированных коэффициентов стереотипности и логической сложности на простом примере.

Пусть нам дан алгоритм, формы записи которого, приведены на (рис. 13.4). /Pict 13-13/ Как видно общее число составляющих элементов алгоритма N = 7, число элементарных операторов N0 = 5 и число логических условий Nл = 2. /Pict 13-14/

Рис. 13.4 Формы записи алгоритма

Для вычисления коэффициента стереотипности Zн разобъем алгоритм на группы, начиная с первого элементарного оператора А и заканчивая логическим условием Р (перед следующим А) (рис. 13.5). /Pict 13-15/

Рис. 13.5 Разбивка алгоритма на группы при вычислении коэффициента стереотипности

При этом необходимо иметь в виду, что алгоритм всегда должен заканчиваться не элементарным оператором, а логическим условием, так как после любого элементарного оператора (действия) предполагается всегда наступление логического условия. Поэтому общее число составляющих алгоритма будет N=8. Тогда, исходя из результатов разбивки алгоритма, приведённых на этом рисунке, можно рассчитать коэффициент стереотипности: /Pict 13-16/ и /Pict 13-17/

.

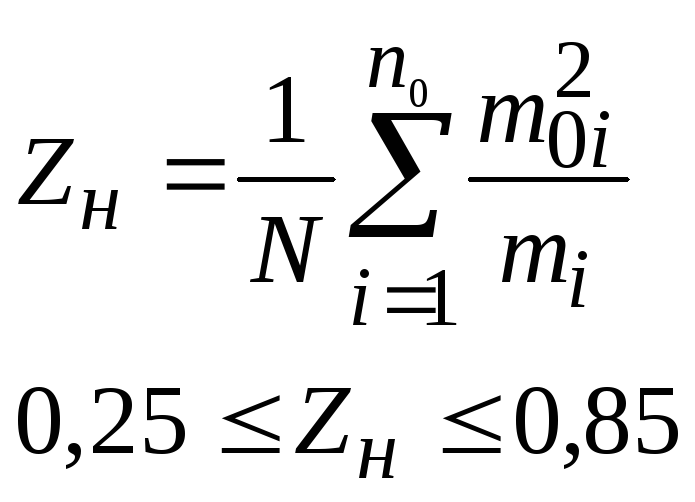
Условие обеспечивается.

Для вычисления коэффициента логической сложности Lн разобъем алгоритм на группы, начиная с первого логического условия P и заканчивая элементарным оператором А (перед следующим Р) (рис.13.6). /Pict 13-18/

Рис. 13.6 Разбивка алгоритма на группы при вычислении коэффициента логической сложности

При этом необходимо иметь в виду, что первый элементарный оператор в данном случае не учитывается. Поэтому общее число составляющих алгоритма будет N* =7. Тогда, исходя из результатов разбивки алгоритма, приведенных на этом рисунке, можно рассчитать коэффициент логической сложности: /Pict 13-19/ и /Pict 13-20/

.

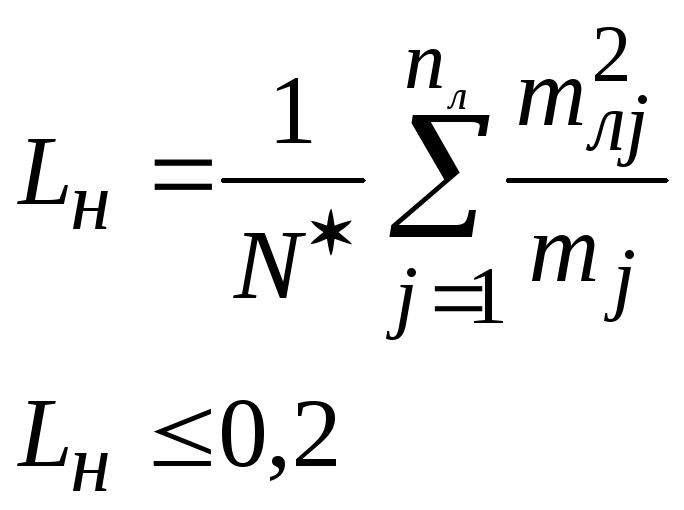
Условие не обеспечивается.