
Роль математического моделирования
.pdf
Общероссийский конкурс на лучший реферат
по теме
«Инновационные медицинские технологии»
Номинация:
«Смежные направления»
Тема реферата:
«Роль математических моделей в медицине»
Работу выполнила:
Ахметова Юлия Андреевна
студентка 3-го курса Волжского политехнического института (филиала)
Государственного образовательного учреждения высшего профессионального образования
«Волгоградский государственный технический университет»
yahmetova@yandex.ru
Научный руководитель:
Мустафина Джамиля Алиевна
старший преподаватель кафедры «Математика» Волжского политехнического института (филиала)
Государственного образовательного учреждения высшего профессионального образования
«Волгоградский государственный технический университет»
dzamilyam@mail.ru
АННОТАЦИЯ
К современной медицине предъявляют высокие требования, как к квалификации врачей, так и используемым методикам. Общее количество
информации о болезнях увеличивается с каждым годом и один человек не в состоянии в точности оценить важность имеющегося материала для врачебной практики и тогда приходит на помощь математика, которая помогает структурировать материал. Выбор тех или иных математических
моделей при описании и исследовании медицинских объектов зависит от индивидуальных знаний специалиста и от особенностей решаемых задач.
Методы оптимизации позволяют выявить режимы работы конструкции, при которых обеспечиваемое механическое воздействие
способно значительно сократить сроки коррекции деформированного позвоночника.
Численные методы оказываются не только наиболее точными, но и позволяют наиболее корректно строить вычислительные алгоритмы, что не маловажно при диагностике болезней.
Чтобы имитировать переходный процесс изменения силы мышцы, возникающий при изменении ее длины, Hill A.V. построил модель мышечного волокна, состоящую из контрактильного элемента, соединенного с последовательным упругим элементом.
Применение дифференциальных уравнений в медицине демонстрируются на примере простейшей математической модели эпидемии.
В модели описывается распространение инфекционного заболевания в изолированной популяции.
Математический подход не только облегчает точное количественное описание определенной задачи путем построения той или иной подходящей модели, но и дает средство к решению поставленной задачи.
Степень разработанности математических методов в научной дисциплине служит объективной характеристикой глубины знаний об изучаемом предмете.
2
ОГЛАВЛЕНИЕ
Аннотация . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 Оглавление. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 I. Области применения математических методов . . . . . . . . . . . . . . . . . . . 7
II. Методы оптимизации - моделирование процесса коррекции
8
деформации позвоночника аппаратом внешней фиксации . . . . . . . . . . .
III. Численное моделирование . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 IV. Модель Хилла . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 V. Математическая модель эпидемии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 Вывод . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . 15 Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
3
ВВЕДЕНИЕ
Степень разработанности математических методов в научной дисциплине служит объективной характеристикой глубины знаний об изучаемом предмете. Явления в физики и химии описываются математическими моделями достаточно полно, в результате эти науки достигли высокой степени теоретических обобщений.
Математическое моделирование как нормальных физиологических, так
и патологических процессов является в настоящее время одним из самых актуальных направлений в научных исследованиях. Дело в том, что
современная медицина представляет собой в основном экспериментальную науку с огромным эмпирическим опытом воздействия на ход тех или иных болезней различными средствами. Что же касается подробного изучения процессов в биосредах, то их экспериментальное исследование является ограниченным, и наиболее эффективным аппаратом их исследования представляется математическое моделирование.
Попытки использовать математическое моделирование в биомедицинских направлениях начались в 80-х гг. 19 в. Идея корреляционного анализа, выдвинутая английским психологом и
антропологом Гальтоном и усовершенствованная английским биологом и математиком Пирсоном, возникла как результат попыток обработки биомедицинских данных. Начиная с 40-х гг. 20 в. математические методы проникают в медицину и биологию через кибернетику и информатику.
Первым примером упрощенного описания живых систем в медицине и биологии была модель черного ящика, когда все выводы делались только на основе изучения реакций объекта (выходов) на те или иные внешние воздействия (входы) без учета внутренней структуры объекта. Соответствующее описание объекта в понятиях вход — выход оказалось неудовлетворительным, т.к. оно не учитывало изменения его выходных реакций на одно и то же воздействие из-за влияния внутренних изменений в
4
объекте. Поэтому метод черного ящика уступил место методам пространства состояний, в которых описание дается в понятиях вход — состояние — выход. Наиболее естественным описанием динамической системы в рамках теории пространства состояний является компартментальное моделирование, где каждому компартменту соответствует одна переменная состояния. В то же время соотношения вход — выход по-прежнему широко используются для описания существенных свойств биологических объектов.
Выбор тех или иных математических моделей при описании и исследовании биологических и медицинских объектов зависит как от индивидуальных знаний специалиста, так и от особенностей решаемых задач. Например, статистические методы дают полное решение задачи во всех случаях, когда исследователя не интересует внутренняя сущность процессов, лежащих в основе изучаемых явлений. Когда знания о структуре системы, механизмах ее функционирования, протекающих в ней процессах и
возникающих явлениях могут существенно повлиять на решения исследователя, прибегают к методам математического моделирования систем.
Под руководством И.М. Гельфанда был развит целый подход,
позволяющий формализовать врачебные знания на основе гипотезы структурной организации данных о человеке, и таким путем получать в клинической медицине результаты, сравнимые по своей строгости с результатами экспериментальных наук, при полном соблюдении этических законов медицины.
Широко применяются математические методы в биофизике, биохимии, генетике, физиологии, медицинском приборостроении, создании биотехнических систем. Развитие математических моделей и методов способствует: расширению области познания в медицине; появлению новых высокоэффективных методов диагностики и лечения, которые лежат в основе разработок систем жизнеобеспечения; созданию медицинской техники.
5
В последние годы активное внедрение в медицину методов математического моделирования и создание автоматизированных, в том числе и компьютерных, систем существенно расширило возможности диагностики и терапии заболеваний.
Одной из разновидностей медицинских компьютерных диагностических систем является диагностика с постановкой конкретного диагноза на основе имеющейся информации.
При математическом моделировании выделяют два независимых круга задач, в которых используют модели. Первый носит теоретический характер и направлен на расшифровку структуры систем, принципов ее функционирования, оценку роли и потенциальных возможностей конкретных регуляторных механизмов.
Другой круг задач имеет практическую направленность. В медицине они применяются, например, с целью получения конкретных рекомендаций для индивидуального больного или группы однородных больных:
определение оптимальной суточной дозы препарата для данного больного при различных режимах питания и физической нагрузки.
6
I.Области применения математических методов [3]
Потребность в математическом описании появляется при любой попытке вести обсуждение в точных понятиях и даже если это касается таких сложных областей, как искусство и этика.
Важен вопрос о том, в каких областях медицины применимы математические методы. Примером может служить область медицинской диагностики. Для постановки диагноза врач совместно с другими
специалистами часто бывает вынужден учитывать самые разнообразные факты, опираясь отчасти на свой личный опыт, а отчасти на материалы, приводимые в многочисленных медицинских руководствах и журналах.
Общее количество информации увеличивается со все возрастающей интенсивностью, и есть такие болезни, о которых уже столько написано, что один человек не в состоянии в точности изучить, оценить, объяснить и
использовать всю имеющуюся информацию при постановке диагноза в каждом конкретном случае и тогда приходит на помощь математика, которая помогает структурировать материал. В тех случаях, когда задача содержит большое число существенных взаимозависимых факторов, каждый из которых в значительной мере подвержен естественной изменчивости, только
с помощью правильно выбранного статистического метода можно точно описать, объяснить и углубленно исследовать всю совокупность взаимосвязанных результатов измерений.
Если число факторов или важных результатов настолько велико, что
человеческий разум не в состоянии их обработать даже при введении некоторых статистических упрощений, то обработка данных может быть произведена на электронной вычислительной машине.
7
II.Методы оптимизации - моделирование процесса коррекции
деформации позвоночника аппаратом внешней фиксации [1]
Современная травматология и ортопедия широко используют устройства механического воздействия при лечении различного рода травм и патологий. В частности для коррекции деформаций позвоночника внедрён аппарат внешней фиксации, конструкция которого обладает высокой степенью статической неопределимости.
Моделирование (от лат. modulus — мера, образец) — процесс создания моделей, схем, знаковых или реальных аналогов, отражающих существенные свойства более сложных объектов (прототипов). Служит исследовательским инструментарием для изучения отдельных аспектов и свойств прототипа.
Выбор математической модели оптимизации того или иного процесса предполагает учёт целого спектра составляющих параметров, способных оказывать влияние на качественные стороны рассматриваемого процесса.
Строить математическую модель необходимо с использованием данных о распределении усилий коррекции, напряжении в опасных сечениях, усилиях возникающих со стороны внешних связей – сегментов позвоночника. В
частности существует методика получения зависимости между изменениями формы искривлённого позвоночника и действием изгибающего момента в его сечениях. В качестве целевой функции оптимизации перевода аппарата
из одного пространственного положения в другое принято время совершения процесса. Необходимо выявить ограничения по прочности, исходному параметру деформации, рабочему диапазону усилий коррекции, изменению параметра деформации в ходе коррекции.
Под результатами оптимизации подразумеваются величины усилий коррекции, при которых значение целевой функции изменения времени в условиях поставленных ограничений минимально (рис 1).
8
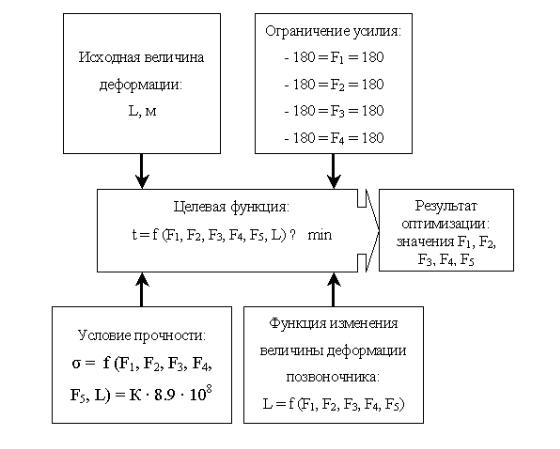
Рис. 1. Блок-схема оптимизации процесса перевода аппарата из одного пространственного положения в другое F1, F2 , F3 , F4 , F5 - усилия коррекции, (H); L – величина деформации.
Таким образом, математическое моделирование процесса изменения
пространственного положения аппарата внешней фиксации позвоночника позволяет выявить режимы работы конструкции, при которых
обеспечиваемое механическое воздействие способно значительно сократить сроки коррекции деформированного позвоночника.
III.Численное моделирование [6]
Среди численных методов наиболее широко используются в вычислительной практике — метод верхней релаксации, трёхслойный метод Чебышева, метод Дугласа–Ренфорда, попеременно-треугольный метод, многосеточный метод.
9
Наибольшие трудности при численном решении вызывают системы уравнений в частных производных гиперболического типа (механика сплошных сред). Эффективными для численного решения такого класса задач являются сеточно-характеристические методы, которые рассмотрены в работах Головизина В.М., Карабасова С.А., Петрова И.Б., Толстых А.И., Холодова А.С. и т. д. Эти методы оказываются не только наиболее точными,
но и позволяют наиболее корректно строить вычислительные алгоритмы на границах области интегрирования и границах раздела сред. Одним из
наиболее важных показателей качества численного решения является его близость к точному вблизи областей с большими градиентами решений.
Численное изучение биомедицинских процессов, показали
эффективность использования численного моделирования при решения задач на основе системы уравнений механика сплошных сред и методов,
учитывающих характеристические свойства систем уравнений гиперболического типа.
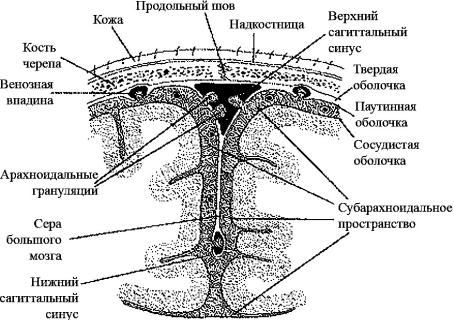
На рис. 2 представлена схема черепно-мозговой системы, которая выбиралась для моделирования последствий черепно-мозговых травм.
рис.2. Схема черепно-мозговой системы, которая выбиралась для моделирования
последствий черепно-мозговых травм.
10
