ИДЗ_2_ТЕОР_ВЕР_Модуль_2_2008_2_VERSION
.doc
Контрольная
работа №2 по теории вероятностей. стр.
1. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Вариант
1-30. Задан
закон распределения дискретных случайных
величин
и
(в первой и второй строке заданы возможные
значения величин
и
,
а в третьем вероятности этих значений).
Найти:
-
для случайных величин
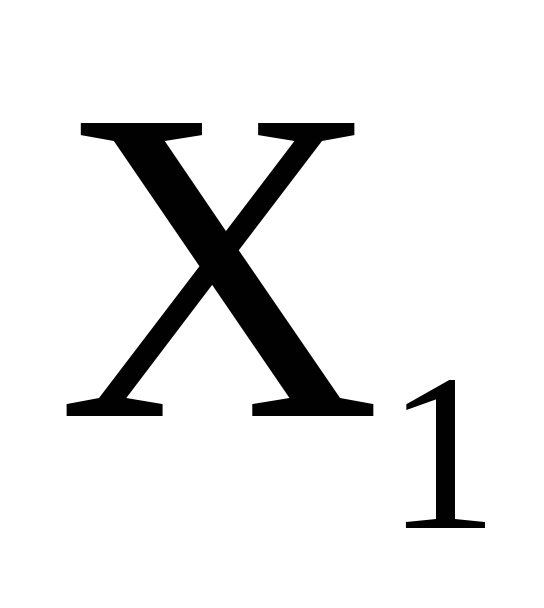
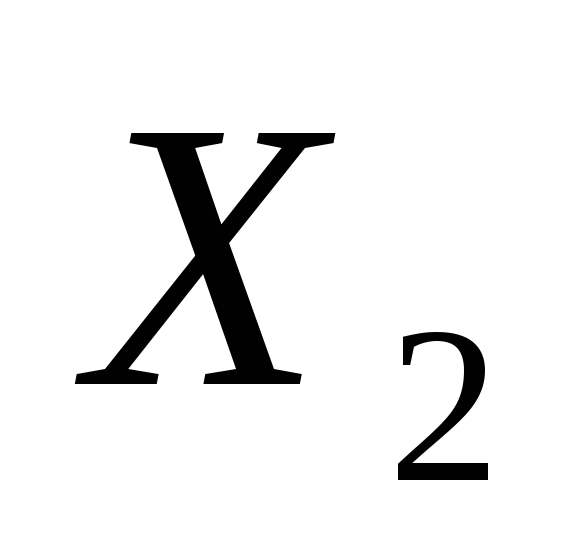построить функции распределения
; -
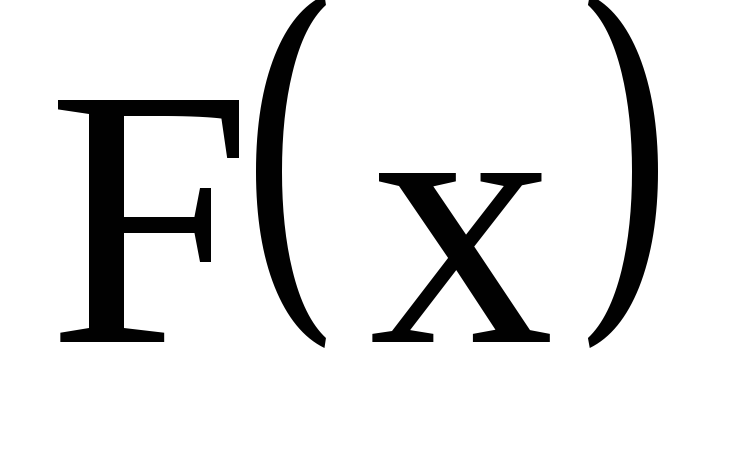математические ожидания
,
; -
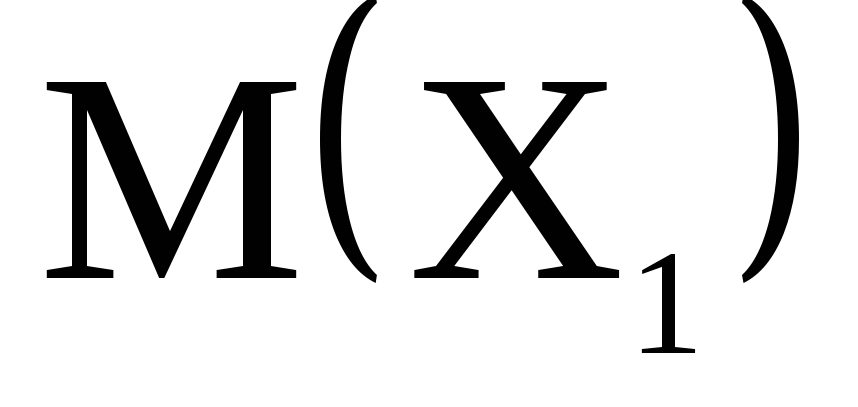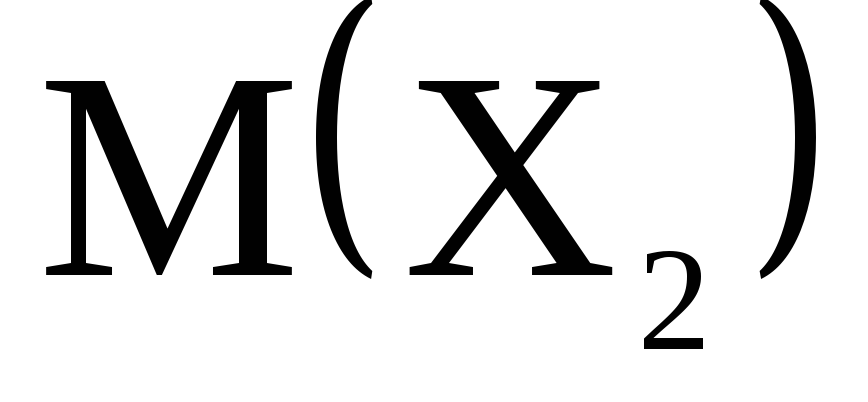дисперсии
,
;
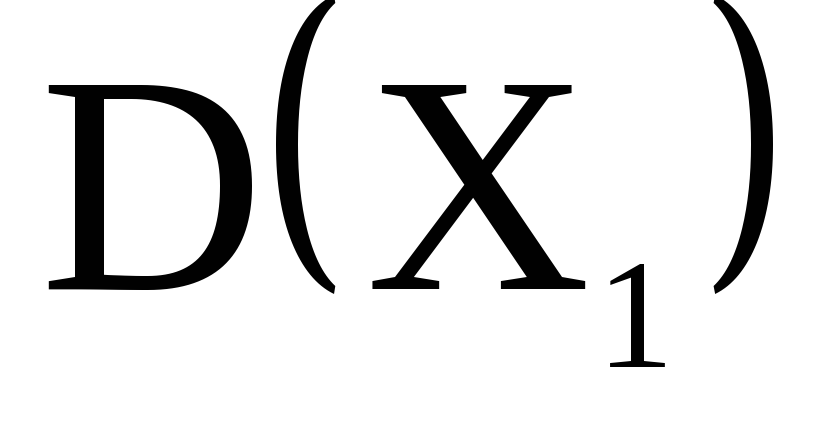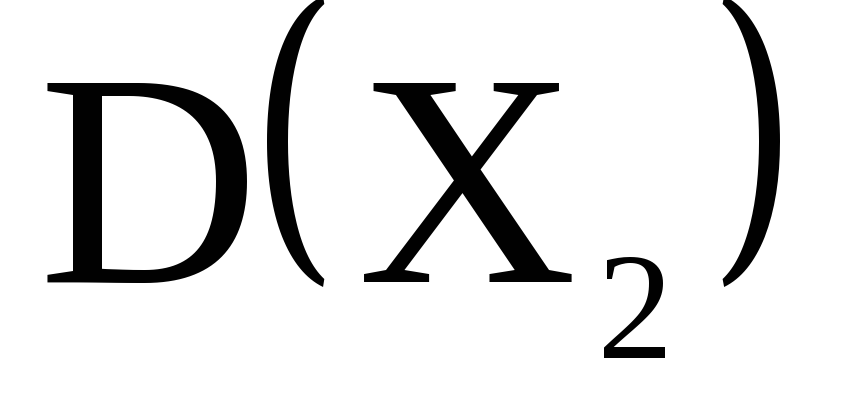среднеквадратичные отклонения
,
;
|
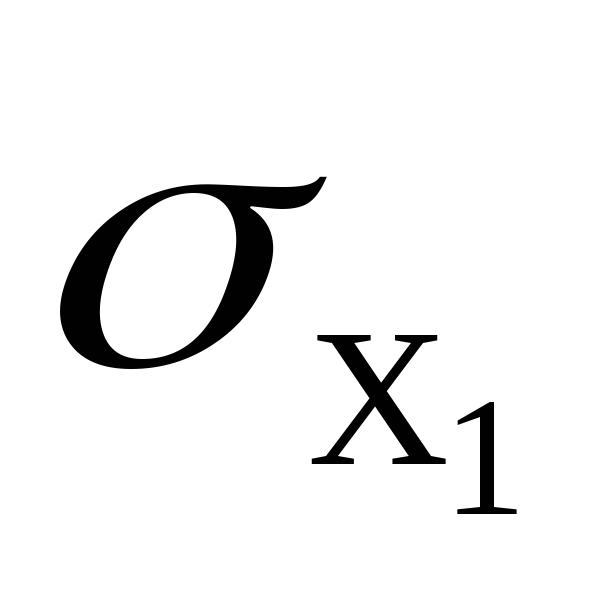Вариант |
Закон распределения |
|||||
|
1 |
|
5 |
6 |
7 |
8 |
9 |
|
|
11 |
14 |
13 |
17 |
22 |
|
|
|
0,1 |
0,2 |
0,25 |
0,25 |
0,2 |
|
|
2 |
|
10 |
15 |
20 |
25 |
30 |
|
|
14 |
18 |
21 |
27 |
32 |
|
|
|
0,2 |
0,1 |
0,1 |
0,3 |
0,3 |
|
|
3 |
|
2 |
4 |
6 |
8 |
10 |
|
|
21 |
17 |
15 |
7 |
5 |
|
|
|
0,1 |
0,3 |
0,3 |
0,2 |
0,1 |
|
|
4 |
|
1 |
5 |
8 |
10 |
11 |
|
|
25 |
20 |
15 |
12 |
10 |
|
|
|
0,3 |
0,1 |
0,2 |
0,1 |
0,3 |
|
|
5 |
|
10 |
20 |
30 |
40 |
50 |
|
|
4 |
12 |
17 |
19 |
27 |
|
|
|
0,2 |
0,1 |
0,2 |
0,2 |
0,3 |
|
|
6 |
|
12 |
15 |
18 |
20 |
25 |
|
|
24 |
19 |
15 |
12 |
9 |
|
|
|
0,15 |
0,2 |
0,3 |
0,2 |
0,15 |
|
|
7 |
|
4 |
7 |
10 |
13 |
20 |
|
|
12 |
15 |
20 |
25 |
33 |
|
|
|
0,3 |
0,2 |
0,2 |
0,15 |
0,15 |
|
|
8 |
|
20 |
25 |
30 |
35 |
40 |
|
|
9 |
15 |
17 |
18 |
23 |
|
|
|
0,3 |
0,15 |
0,1 |
0,15 |
0,3 |
|
|
Вариант |
Закон распределения |
|||||
|
9 |
|
1 |
2 |
3 |
4 |
5 |
|
|
6 |
11 |
13 |
18 |
27 |
|
|
|
0,1 |
0,2 |
0,25 |
0,25 |
0,2 |
|
|
10 |
|
11 |
13 |
15 |
16 |
19 |
|
|
10 |
8 |
6 |
4 |
3 |
|
|
|
0,2 |
0,1 |
0,1 |
0,3 |
0,3 |
|
|
11 |
|
21 |
25 |
27 |
28 |
30 |
|
|
13 |
16 |
18 |
19 |
21 |
|
|
|
0,1 |
0,3 |
0,3 |
0,2 |
0,1 |
|
|
12 |
|
10 |
15 |
20 |
30 |
50 |
|
|
10 |
8 |
7 |
6 |
5 |
|
|
|
0,3 |
0,1 |
0,2 |
0,1 |
0,3 |
|
|
13 |
|
2 |
5 |
8 |
11 |
12 |
|
|
10 |
16 |
22 |
30 |
35 |
|
|
|
0,2 |
0,1 |
0,2 |
0,2 |
0,3 |
|
|
14 |
|
2 |
4 |
6 |
8 |
10 |
|
|
10 |
15 |
21 |
25 |
31 |
|
|
|
0,15 |
0,2 |
0,3 |
0,2 |
0,15 |
|
|
15 |
|
8 |
11 |
12 |
16 |
17 |
|
|
25 |
21 |
18 |
14 |
12 |
|
|
|
0,3 |
0,2 |
0,2 |
0,15 |
0,15 |
|
|
16 |
|
1 |
3 |
4 |
5 |
8 |
|
|
10 |
32 |
45 |
60 |
75 |
|
|
|
0,3 |
0,15 |
0,1 |
0,15 |
0,3 |
|
|
17 |
|
2 |
5 |
8 |
10 |
15 |
|
|
7 |
19 |
22 |
28 |
35 |
|
|
|
0,1 |
0,3 |
0,3 |
0,2 |
0,1 |
|
|
18 |
|
1 |
3 |
5 |
7 |
9 |
|
|
3 |
5 |
8 |
15 |
20 |
|
|
|
0,2 |
0,1 |
0,2 |
0,2 |
0,3 |
|
|
19 |
|
1 |
2 |
3 |
4 |
5 |
|
|
20 |
18 |
15 |
11 |
8 |
|
|
|
0,15 |
0,2 |
0,3 |
0,2 |
0,15 |
|
|
20 |
|
12 |
15 |
16 |
17 |
20 |
|
|
20 |
29 |
33 |
35 |
38 |
|
|
|
0,3 |
0,15 |
0,1 |
0,15 |
0,3 |
|
|
21 |
|
1 |
2 |
5 |
9 |
10 |
|
|
3 |
5 |
12 |
17 |
22 |
|
|
|
0,1 |
0,3 |
0,3 |
0,2 |
0,1 |
|
|
Вариант |
Закон распределения |
|||||
|
22 |
|
1 |
4 |
5 |
6 |
10 |
|
|
21 |
17 |
11 |
7 |
4 |
|
|
|
0,15 |
0,2 |
0,3 |
0,2 |
0,15 |
|
|
23 |
|
10 |
11 |
12 |
13 |
14 |
|
|
19 |
23 |
26 |
25 |
29 |
|
|
|
0,2 |
0,1 |
0,1 |
0,3 |
0,3 |
|
|
24 |
|
0 |
2 |
5 |
6 |
8 |
|
|
4 |
5 |
9 |
13 |
15 |
|
|
|
0,2 |
0,1 |
0,2 |
0,2 |
0,3 |
|
|
25 |
|
2 |
4 |
6 |
8 |
12 |
|
|
7 |
13 |
15 |
21 |
30 |
|
|
|
0,15 |
0,2 |
0,3 |
0,2 |
0,15 |
|
|
26 |
|
0 |
5 |
15 |
20 |
25 |
|
|
4 |
12 |
35 |
39 |
46 |
|
|
|
0,3 |
0,15 |
0,1 |
0,15 |
0,3 |
|
|
27 |
|
1 |
3 |
4 |
5 |
6 |
|
|
4 |
8 |
13 |
16 |
20 |
|
|
|
0,2 |
0,1 |
0,1 |
0,3 |
0,3 |
|
|
28 |
|
2 |
3 |
5 |
7 |
8 |
|
|
17 |
12 |
9 |
6 |
5 |
|
|
|
0,1 |
0,3 |
0,3 |
0,2 |
0,1 |
|
|
29 |
|
1 |
2 |
3 |
8 |
10 |
|
|
4 |
7 |
10 |
21 |
25 |
|
|
|
0,1 |
0,3 |
0,3 |
0,1 |
0,2 |
|
|
30 |
|
5 |
10 |
12 |
15 |
20 |
|
|
19 |
32 |
40 |
61 |
82 |
|
|
|
0,3 |
0,15 |
0,1 |
0,15 |
0,3 |
|
2. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
2.1
Вариант 1-30.
Случайная величина
задана функцией плотности распределения
.
Найти:
-
коэффициент
; -
функцию распределения
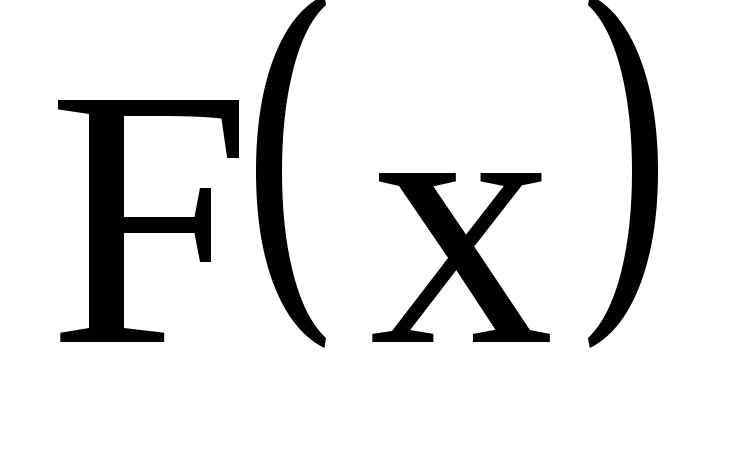и построить её график; -
числовые характеристики случайной величины
:
математическое ожидание
,
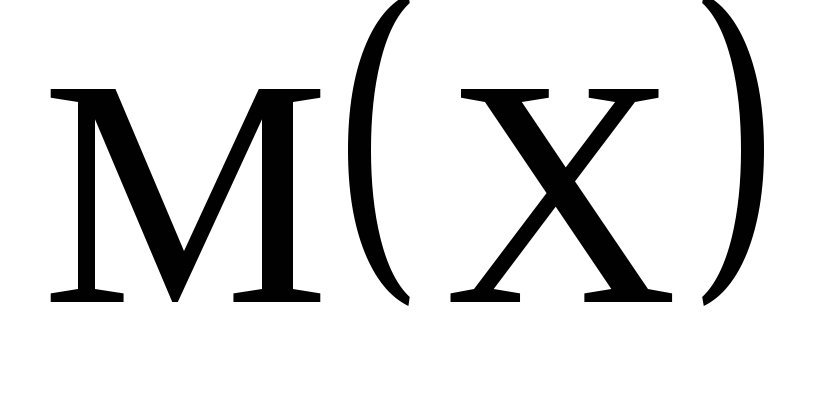дисперсию
,
среднеквадратичное отклонение
; -
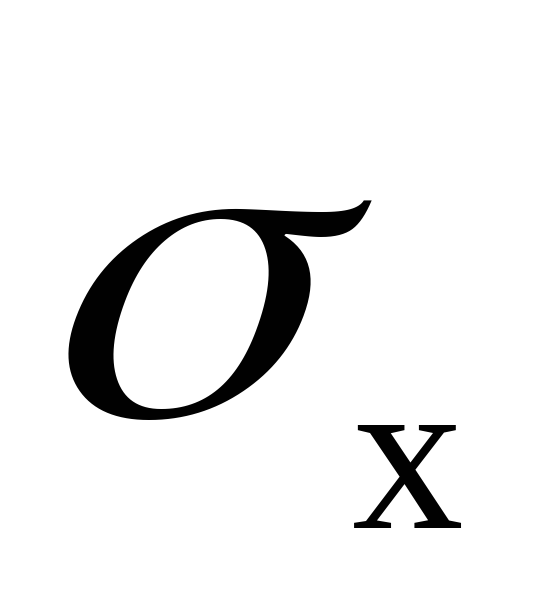вероятность того, что случайная величина находится в интервале
.
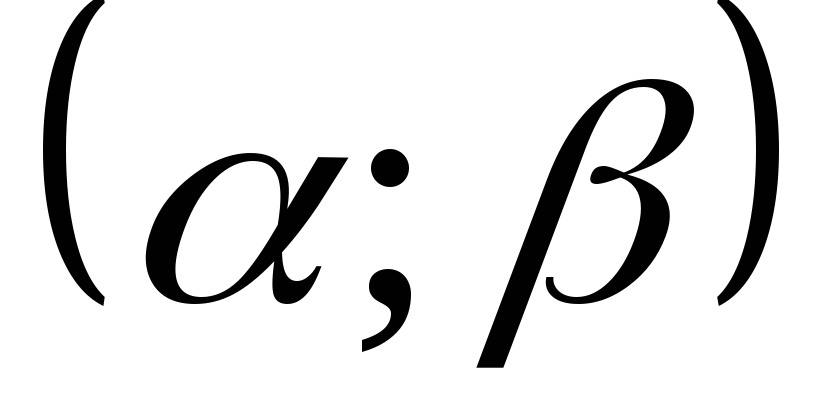