Интегрирование рациональных функций

Рациональной функцией называется функция, равная отношению двух многочленов:

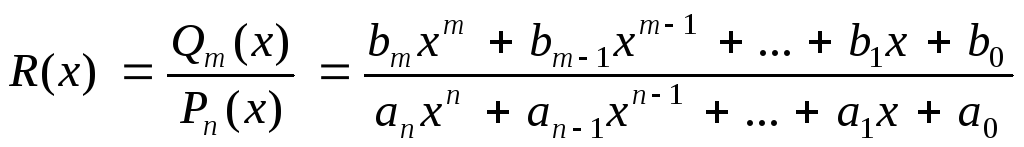(1)

где n, m - целые положительные числа;

Если m < n, то называетсяправильной дробью, если m  n - неправильной дробью.

Всякую неправильную дробь путем деления числителя на знаменатель можно представить в виде суммы некоторого многочлена и правильной дроби:

где - многочлены;- правильная, дробь;l < n.

Так как всякий многочлен легко интегрируется, то интегрирование рациональных функций сводится к интегрированию правильных дробей. Поэтому в дальнейшем будем рассматривать правильные рациональные функции .

Интегрирование правильных рациональных дробей начинают с разложения их на простейшие рациональные дроби.

Простейшей дробью называется дробь одного из следующих четырех типов:

1). ; 2).; 3).; 4).

где A,M,N,a,p,q– постоянные числа;h2 иh– целое;.

Покажем схему нахождения интегралов от простейших рациональных дробей:

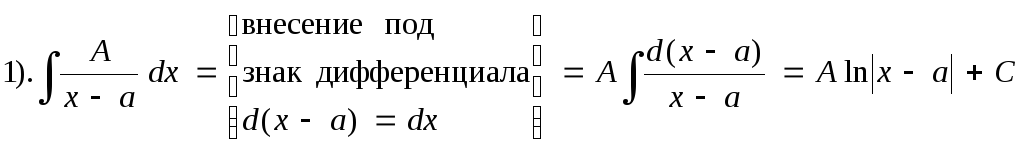
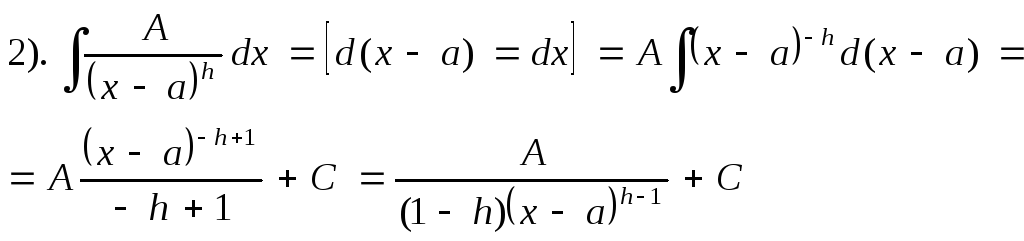
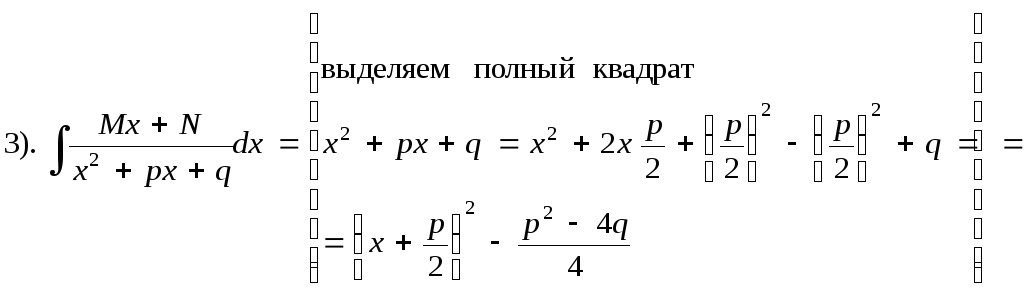
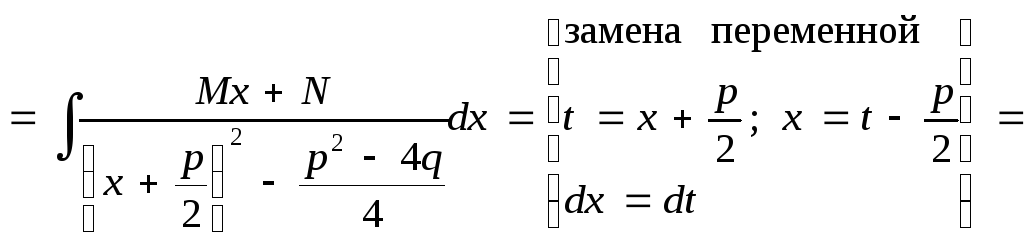
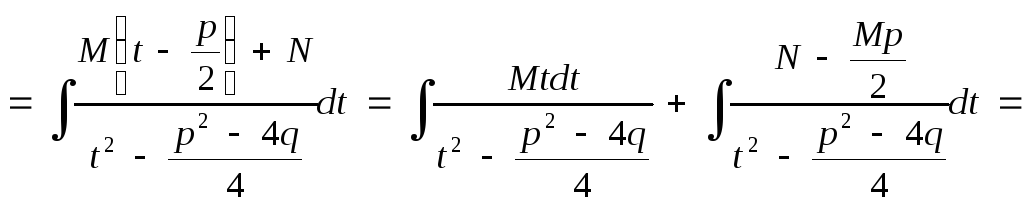
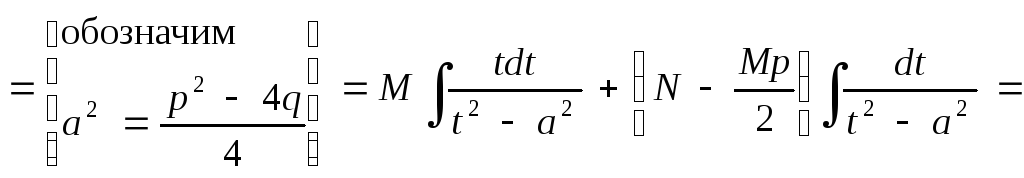
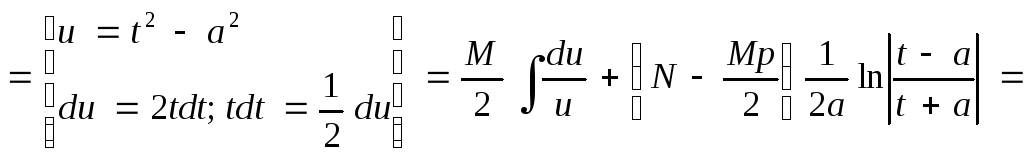
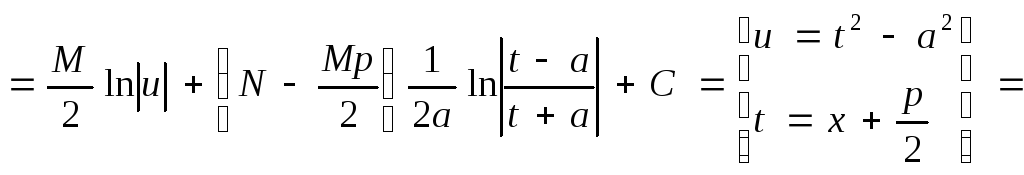
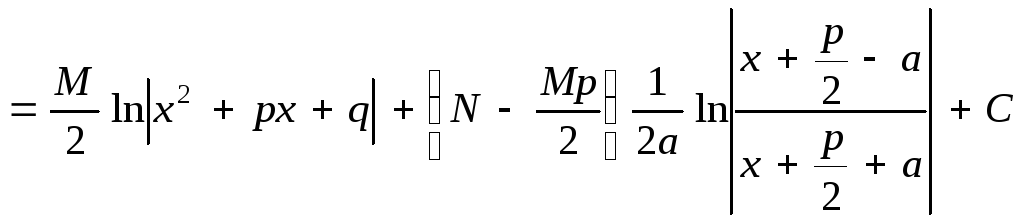
где

Аналогичные приемы используются при интегрировании простейших дробей четвертого типа. При этом задача отыскания интеграла четвертого типа сводится к отысканию интеграла следующего вида

,

где ;, который может быть найден с помощью рекуррентной формулы понижения степени знаменателя

Таким образом, всякая простейшая рациональная дробь может быть проинтегрирована в элементарных функциях.

Известно, что всякий многочлен с действительными коэффициентами на множестве действительных чисел может быть представлен в виде

, (2)

где - действительные корни многочленакратностей, а;

Всякая правильная рациональная дробь (1) со знаменателем, представленным в виде (2), можно разложить в сумму простейших рациональных дробей типа 1)-4). В данном разложении каждому корню кратностимногочлена(множителю) соответствует суммадробей вида

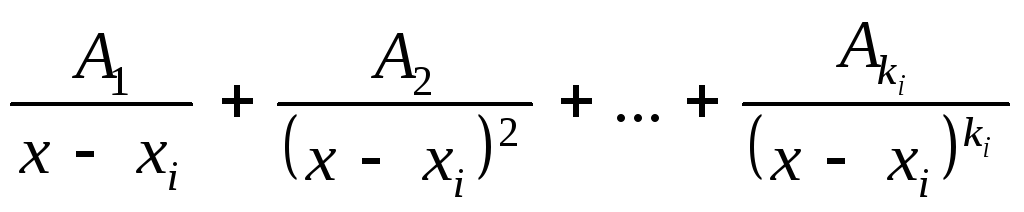(3)

Каждой паре комплексно-сопряженных корней кратности многочлена(множителю) соответствует суммаэлементарных дробей

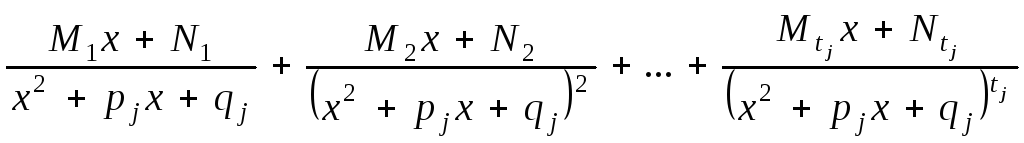(4)

Для вычисления значений A, М, N в разложении функции R(x) на сумму простейших рациональных дробей часто используют метод не­определенных коэффициентов, суть которого заключается в следующем. С учетом формул (3), (4) данную дробь R(x) представим в виде суммы простейших рациональных дробей с неопределенными коэффициентами А, М, N. Полученное равенство является тождеством. Поэтому, если привести все дроби к общему знаменателю в числителе получим многочленстепени (n - 1), тождественно равный многочлену , стоящему в числителе выражения (1). Приравняв коэффициенты при одинаковых степеняхх в этих многочленах, получим систему n уравнений для определения n неизвестных коэффициентов А, М, N (с индексами).

В некоторых случаях с целью упрощения вычислений можно воспользоваться следующим соображением. Так как многочлены итождественно равны, то их значения равны при любых числовых значенияхх. Придавая х конкретные числовые значения, получаем систему уравнений для определения коэффициентов. Такой метод нахождения неизвестных коэффициентов называется методом частных значений. Если значения х совпадают с действительными корнями знаменателя, получаем уравнение с одним неизвестным коэффициентом.

Таким образом, всякая рациональная функция в принципе может быть проинтегрирована указанным выше способом.

В заданиях 3 и 5 необходимо найти интегралы от рациональных функций.

Задание 3. Найти неопределенный интеграл. Результат интегрирования проверить дифференцированием

a). ,b). , c). .

Решение: Во всех примерах задания 3 подынтегральная функция является неправильной рациональной дробью, так как степень многочлена стоящего в числителе больше или равна степени многочлена стоящего в знаменателе. Путем деления числителя на знаменатель выделим целую часть рациональной дроби и правильную рациональную дробь.

Задание 3 a). .

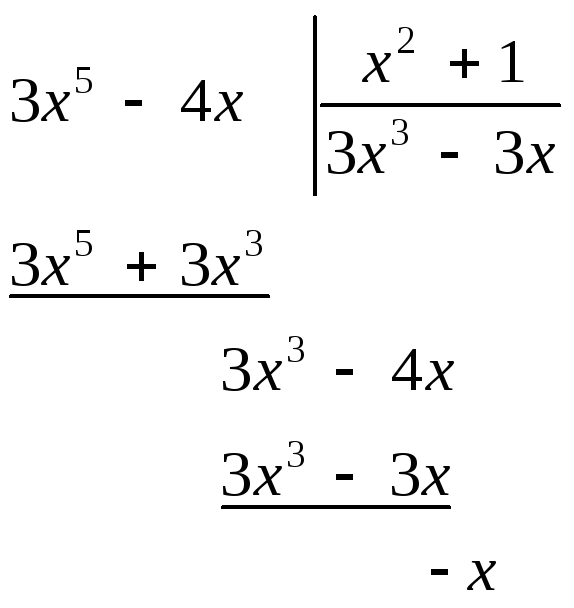
Таким образом . Используя свойство 5⁰, разбиваем исходный интеграл на три интеграла. Первые два являются табличными, где, для первого интеграла, для второго -. Третий интеграл сводится к табличному, где, при помощи внесения под знак дифференциала функции.

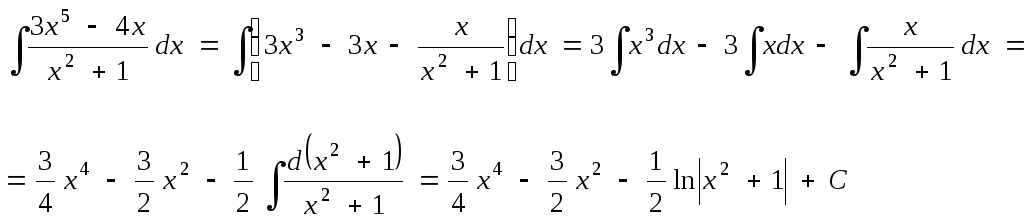
Проверим полученный результат. Продифференцируем

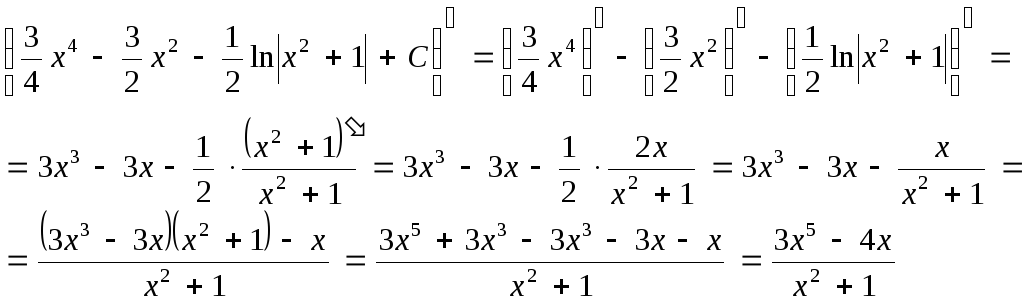Таким образом, производная от неопределенного интеграла равна подынтегральной функции.

Задание 3 b). .

Путем деления числителя на знаменатель выделим целую часть рациональной дроби и правильную рациональную дробь. Разобьем полученный интеграл на два интеграла. Первый является табличным , где,. Второй интеграл является простейшей правильной рациональной дробью третьего типа. Первый этап (выделение полного квадрата в знаменателе) опускается. Подынтегральную функцию разбиваем на сумму двух дробей, после чего второй интеграл представляется в виде суммы двух интегралов. Первый интеграл сводится к табличному, где, при помощи внесения под знак дифференциала функции, второй интеграл является табличным, где,.

Проверка найденного интеграла осуществляется аналогично тому, как это было сделано в пункте а).

Задание 3 c). .

Путем деления числителя на знаменатель выделим целую часть рациональной дроби и правильную рациональную дробь. Разобьем полученный интеграл на три интеграла. Первый и второй интегралы является табличным , где; для первого интеграла, для второго -. Третий интеграл - табличный, где,. Тогда

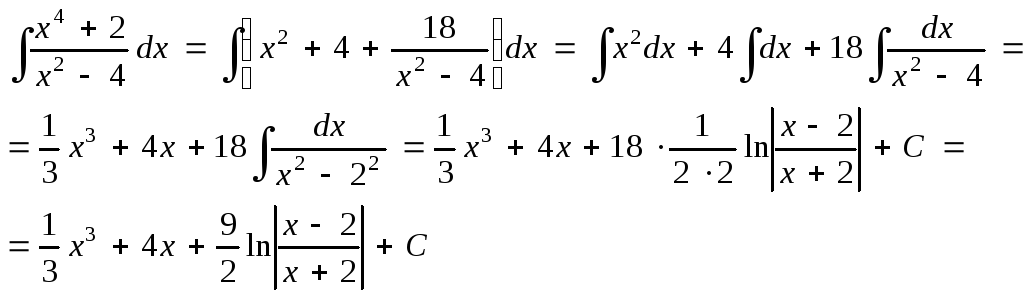
Проверка найденного интеграла осуществляется аналогично тому, как это было сделано в пункте а).

Задание 5. Найти неопределенный интеграл. Результат интегрирования проверить дифференцированием

a). ,b). .

Решение: Во всех примерах задания 5 подынтегральная функция является рациональной дробью. Для интегрирования их воспользуемся разложением подынтегральных дробей на сумму простейших.

Задание 5 a). .

Подынтегральная функция является правильной рациональной дробью, так как степень многочлена стоящего в числителе () меньше степени многочлена стоящего в знаменателе (). Разложим знаменатель подынтегральной функции на множители. Для этого найдем корни квадратного уравнения Тогда . Согласно формуле (3), в разложении правильной дроби на простейшие каждому множителю знаменателя видасоответствует слагаемое. Поэтому в данном случае имеем

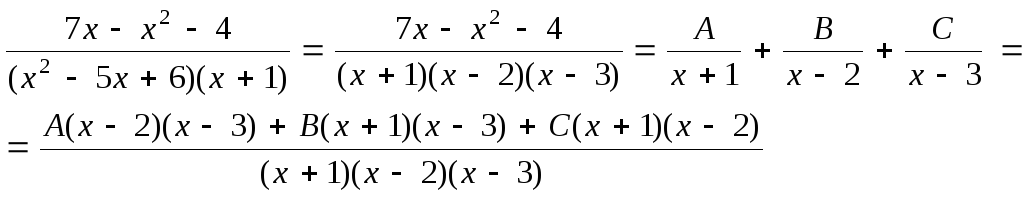
Приведя правую часть разложения на сумму простейших дробей к общему знаменателю, и приравняв числители дробей, получим тождество

Коэффициенты A,B,Cопределим, например, с помощью метода частных значений (подставим одни и те же значенияxв правую и левую часть тождества):

Подставим в тождество. Получим, так как.

Аналогично при получим:; приполучим:.

Таким образом, получаем систему трех уравнений с тремя неизвестными

Подставим найденные коэффициенты в разложение подынтегральной функции на простейшие дроби, получим

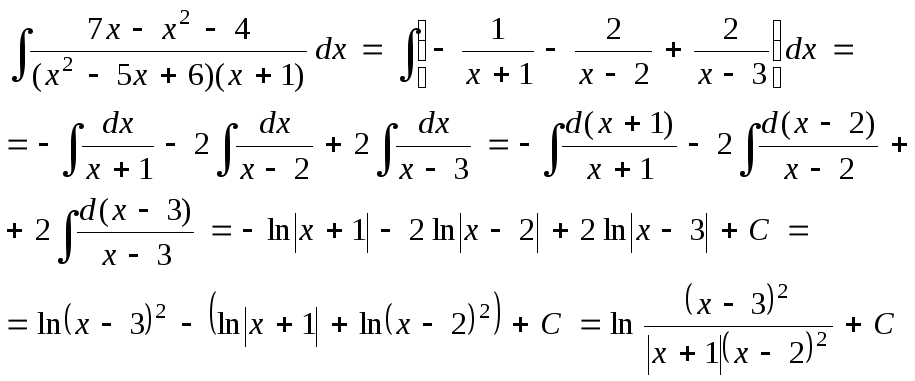
Замечание: результат интегрирования можно оставить в виде суммы логарифмических функций.

Результат интегрирования проверим дифференцированием.

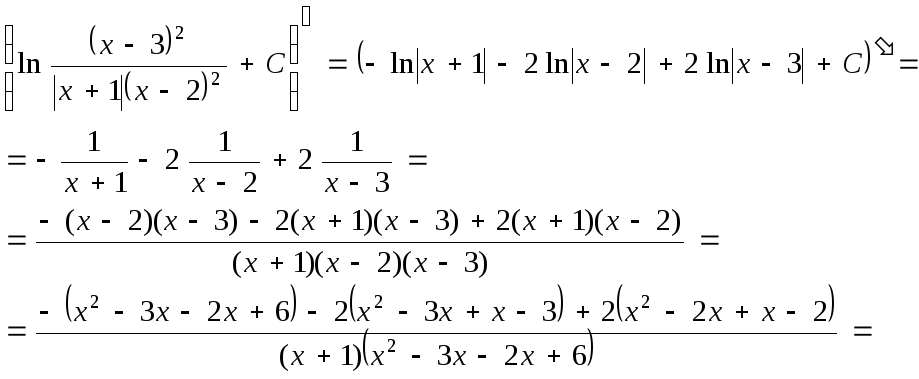
Таким образом, производная от неопределенного интеграла равна подынтегральной функции.

Задание 5 b). .

Так как подынтегральная функция является неправильной дробью (степень многочлена в числителе () больше, чем степень многочлена знаменателя ()), то путем деления числителя на знаменатель можно представить ее в виде суммы целого многочлена и правильной рациональной дроби. Удобно раскрыть скобки в знаменателе и поделить «уголком» числитель на знаменатель.

Так как и, то

Тогда исходный интеграл примет вид

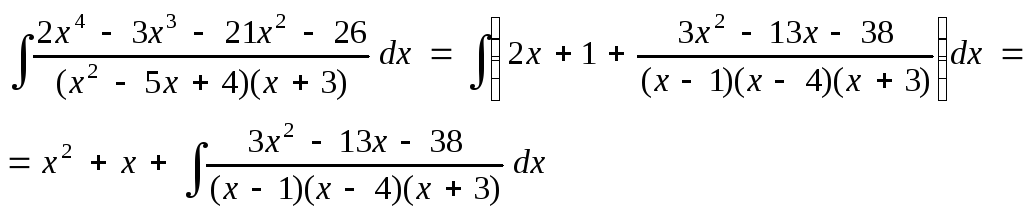
Вычислим отдельно оставшийся интеграл. Подынтегральная функция является правильной рациональной дробью, которая может быть разложена на сумму трех простейших дробей (аналогично тому, как это было сделано в пункте a)).

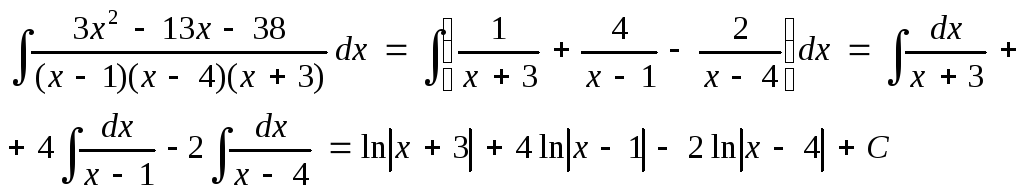
Тогда окончательно получим

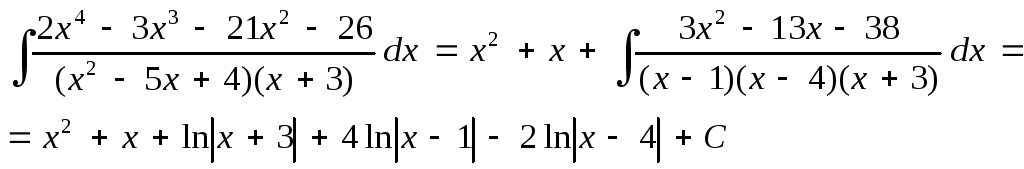
Проверка найденного интеграла осуществляется аналогично тому, как это было сделано в пункте а).