Интегрирование по частям

В этом методе интегрирование осуществляется с помощью формулы

,

где u, v – дифференцируемые функции. Для применения этой формулы подынтегральное выражение разбивается на две части, одну из которых принимают за u, а другую за dv так, чтобы легко находился интеграл от dv и интеграл вычислялся проще, чем исходный.

Рассмотрим два типа интегралов и соответствующие рекомендации по выбору u и dv, для которых формула интегрирования по частям всегда является эффективной, т.е. приводит к более простому интегралу по сравнению с первоначальным. Отметим, что применение формулы интегрирования по частям не ограничивается только этими случаями.

Тип интеграла	Вид интеграла	u	Dv
I
II

Задание 4. Найти неопределенный интеграл. Результат интегрирования проверить дифференцированием

a). ,b). ,

c). d).

Решение: При выполнении задания 4 необходимо воспользоваться формулой интегрирования по частям.

Задание 4 a). .

Данный интеграл является интегралом Iтипа, то есть многочлен первой степениумножается на тригонометрическую функцию. Воспользуемся указанными выше рекомендациями и обозначим черезuмногочлен, то есть, а черезdvоставшеюся часть подынтегрального выражения, то есть. После этого найдеми. Полученный интеграл можно вычислить, используя внесения под знак дифференциалаили свойство 6⁰. Воспользуемся свойством 6⁰, то есть если, то. Так как, то прии , получим. При нахожденииvв формуле интегрирования по частям полагаемCравным нулю, так как необходимо найти не все первообразные, а какую-нибудь одну из них.

Применяя формулу интегрирования по частям , придем к более простому интегралу, который может быть приведен к табличному интегралувнесением под знак дифференциала 5x, либо может быть вычислен, используя указанный табличный интеграл и свойство 6⁰ , как это было показано выше при нахожденииv.

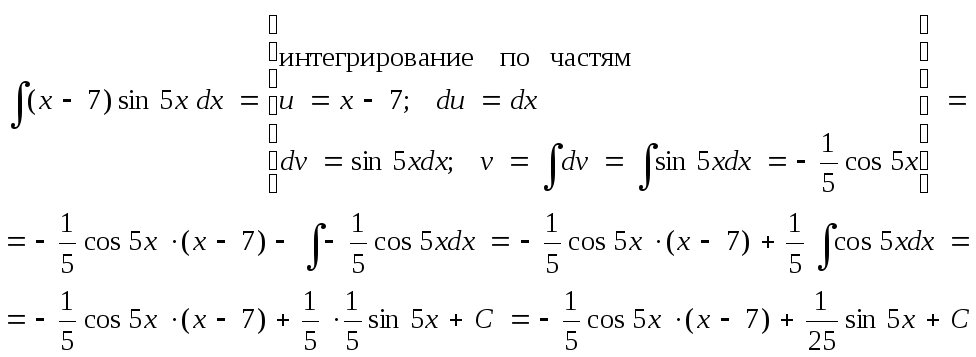
Выполним проверку результата. Найдем производную

Таким образом, производная от неопределенного интеграла равна подынтегральной функции.

Задание 4 b).

Данный интеграл является интегралом II типа, то есть многочлен нулевой степени умножается на обратную тригонометрическую функцию. Воспользуемся указанными выше рекомендациями и обозначим черезu обратную тригонометрическую функцию, то есть , а черезdv оставшеюся часть подынтегрального выражения, то есть . После этого найдеми. Применим формулу интегрирования по частям.

Проверку найденного неопределенного интеграла рекомендуется выполнить самостоятельно.

Задание 4 c).

Данный интеграл является интегралом I типа. Применяем формулу интегрирования по частям, воспользовавшись соответствующими рекомендациями.

Проверку найденного неопределенного интеграла рекомендуется выполнить самостоятельно.

Задание 4 d).

Данный интеграл является интегралом II типа. Применяем формулу интегрирования по частям, воспользовавшись соответствующими рекомендациями.

Проверку найденного неопределенного интеграла рекомендуется выполнить самостоятельно.