Лабораторна робота № 9

Фільтрування суспензії на нутч-фільтрі

Мета роботи – ознайомитися з будовою нутч-фільтра та принципом його роботи; вивчити процес фільтру­вання на періодично діючому фільтрі; визначи­ти константи в рівнянні фільтрування, харак­теристики осаду і фільтрувальної перегородки, продуктивність фільтра та швидкість фільтру­вання.

Основні теоретичні положення

Фільтруванням називають процес розділення неоднорідних систем з твердою дисперсною фазою крізь пористі фільтрувальні перегород­ки, які пропускають дисперсійне середовище (рідину або газ) і зат­римують тверді частинки. Таке розділення, зокрема суспензій, можливе лише тоді, коли до та після фільтрувальної перегородки є різниця тисків Δp, Па, - рушійна сила процесу.

Основним завданням теорії фільтрування є визначення швид­кості фільтрування - тобто об'єму фільтрату, який отримують з 1 м² поверхні фільтрувальної перегородки за одиницю часу:

, (9.1)

де w - швидкість фільтрування, м³/(м² · с); V - об’єм фільтрату, м³; F - площа поверхні фільтрувальної перегородки, м²; τ - три­валість фільтрування, с.

Теоретичне визначення швидкості фільтрування базується на припущен-ні, що в капілярах осаду рух рідини відповідає ламінарному режиму. Звідси випливає, що витрата фільтрату V₁, м³/с, крізь один капіляр з радіусом R і довжиною l підпорядковується рівнянню Пуазейля

, (9.2)

де μ - коефіцієнт динамічної в’язкості фільтрату, Па · с.

Якщо на 1 м² площі фільтра буде z капілярів, то елементарний об’єм рідини, що проходить крізь поверхню фільтра площею F за час dτ,

. (9.3)

Застосовуючи загальне кінетичне рівняння, згідно з яким швидкість процесу прямо пропорційна рушійній силі й обернено пропорційна опору, дістанемо

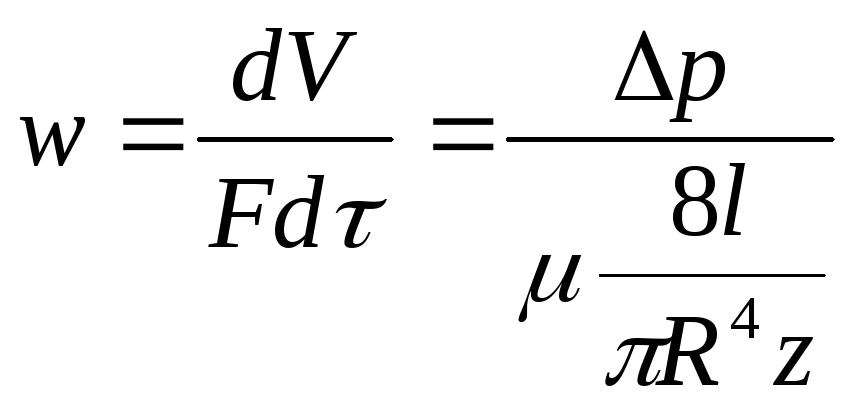. (9.4)

Геометричний комплекс характеризує опір шару осаду, м^-1. У загальному випадку до цього опору додається опір фільтру­вальної перегородки R_п, м^-1. Тоді опір фільтруванню цієї суспензії буде дорівнювати добутку μ(R_o + R_n). Отже,

. (9.5)

Опір R_n можна з достатнім наближенням вважати постійним. Опір шару осаду пропорційний його товщині h_o (за умови одно­рідності структури осаду), тобто

, (9.6)

де r_o - питомий об’ємний опір, який чинить потоку фільтрату з μ = 1 Па · с рівномірний шар осаду завтовшки 1 м, м^-2; х_o = V_o/V - відношення об’єму осаду V_o, що на фільтрувальній перегородці, до об’єму отриманого фільтрату V, м³/м³.

Підставляючи вираз (9.6) у рівняння (9.5), дістаємо основне диференціальне рівняння процесу фільтрування

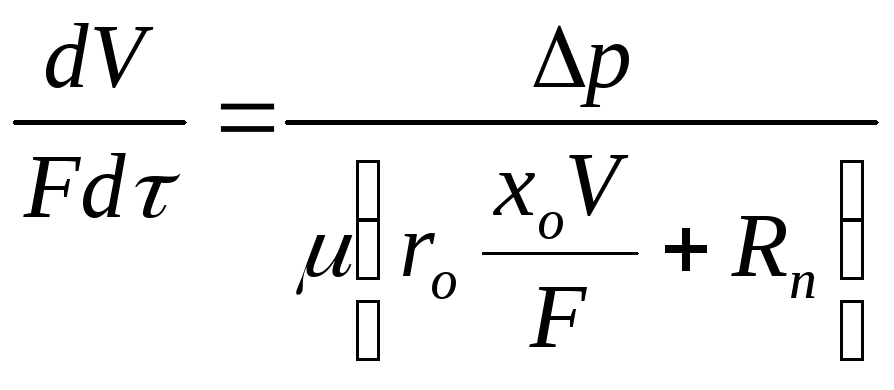. (9.7)

Під час фільтрування питомий опір нестисливих осадів r_o не змінюється, а стисливих - змінюється. Стисливість осаду пояс­нюється деформацією частинок та їх перегрупуванням під впливом тиску і, як наслідок, зумовлює зменшення пористості шару осаду ε - відношення об’єму пор V_п до загального об’єму осаду V_o:

, (9.8)

де V_ч — об’єм частинок осаду.

Під час фільтрування з утворенням осаду найчастіше розрізня­ють два режими роботи: а) при постійній різниці тисків (Δр = const); оскільки зі збільшенням h_o, опір фільтруванню підвищу­ється, швидкість фільтрування зменшується; б) при постійній швидкості (w = const); щоб підтримувати сталу швидкість при зро­стаючому опорі фільтруванню за рахунок зростання h_o, треба збіль­шувати рушійну силу процесу.

При Δр = const із рівняння (9.7) після його інтегрування в ме­жах від 0 до V і від 0 до τ дістанемо

. (9.9)

Це рівняння можна застосувати як до стисливих, так і до не­стисливих осадів. Поділивши всі члени рівняння (9.9) на F², дістанемо

(9.10)

або

, (9.11)

де q - питома продуктивність фільтра (за фільтратом), м³/м², q = V/F; С - константа фільтрування, яка характеризує гідравліч­ний опір фільтрувальної перегородки, м³/м², С = R_п/(r_ox_o); K - константа фільтрування, яка враховує режим процесу фільтрування і фізико-хімічні властивості осаду та рідини, м²/с, К = 2Δр/(μr_ox_o).

Поділивши всі члени рівняння (9.11) на Кq, отримаємо рівнян­ня, яке застосовується для визначення констант фільтрування К і С за дослідними даними:

. (9.12)

Графічно це рівняння виражається прямою лінією АВ, що нахи­лена до горизонтальної осі під кутом α, тангенс якого дорівнює 1/К, і відсікає на осі ординат відрізок 2С/К (див. рис. 9.1).

Знайдені значення К і С дають змогу обчислити за рівнянням (9.11) величину q, а потім продуктивність фільтра V_ф, м³/с:

. (9.13)

Питомий опір осаду r_o визначають із виразу для К, а опір філь­трувальної перегородки R_n - із виразу для С. Опір фільтрувальної перегородки R_п можна визначити також під час фільтрування води при відомих різниці тисків і площі поверхні фільтрування. Щоб визначити оптимальну тривалість фільтрування та середню швид­кість фільтрування, будуємо графічну залежність q = f(τ) (рис. 9.2). На осі вліво від точки 0 відкладаємо відрізок ОL, який дорівнює τ_д - тривалості допоміжних операцій для підготовки фільтра до роботи (складання і розбирання фільтра). З точки L проводимо до­тичну до кривої q = f(τ). Перпендикуляр, проведений з точки доти­ку М на вісь τ, відсікає на ній відрізок, я

кий дорівнює оптималь­ній тривалості процесу фільтруванняτ_опт.

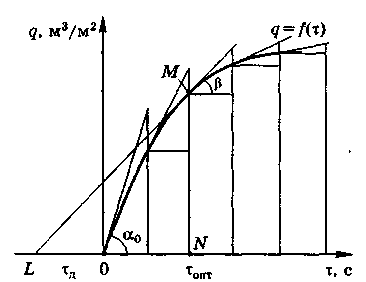
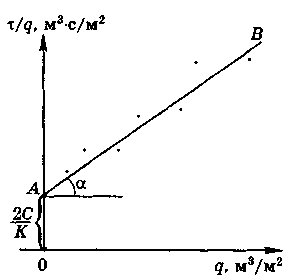
Середня швидкість фільтрування w_c за час τ визначається з рівняння

. (9.14)

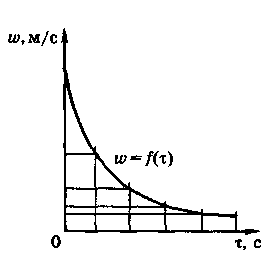
Визначений інтеграл у цьому рівнянні дорівнює площі криволінійної трапеції Φ, мм², яка обмежена графі­ком кривої w = f(τ) (рис. 9.3), крайні­ми ординатами та віссю абсцис.

, (9.15)

Рис. 9.3.Графік залежності швид-кості від тривалості фільтрування

де М_ф - масштаб площі, м³/(м² · мм²), М_ф = М_wМ_τ; М_w - масштаб швидкості, м³/(м² · с · мм); М_τ - масштаб тривалості фільтрування, с/мм

Для побудови графічної залежності w = f(τ) продиференціюємо функцію q = f(τ). На графіку кривої (див. рис. 9.2) з 5-7 її точок, вибраних довільно (наприклад з однаковим кроком по осі абсцис), проводимо дотичні й визначаємо тангенси кутів, що утворюють ці дотичні з додатним напрямом осі абсцис. Ці значення тангенсів кутів дорівнюють миттєвим швидкостям фільтрування у вибраних точках, починаючи з 0:

, (9.16)

де і - номер вибраної точки.