
Algebra_i_geometriya / І модуль / NE_1.2 / Завдання для контролю і самоконтролю
.DOCПитання та завдання для поточного самоконтролю
та контролю знань
Питання:
1. Сформулюйте означення алгебраїчної операції (дії) на множині. Які три необхідні та достатні умови повинні виконуватися, щоб вказане правило задавало алгебраїчну операцію на множині?
2. Опишіть властивості асоціативності та комутативності алгебраїчної операції.
3. Сформулюйте означення нейтрального елемента. Коли нейтральний щодо операції елемент єдиний?
4. Сформулюйте означення нейтралізуючого до заданого елемента. Коли нейтралізуючий елемент єдиний?
5. Які елементи називаються оборотними щодо вказаної операції? Коли їх можна шукати?
6. Сформулювати означення групи.
7. Яка група називається абелевою?
8. Що називають порядком групи? Яку групу називають скінченною (нескінченною)?
9. Сформулювати означення порядку елемента групи. Яка основна властивість порядку елемента скінченної групи?
10. Сформулюйте означення підгрупи.
11. Сформулюйте означення циклічної підгрупи, циклічної групи. Дайте означення твірного елемента циклічної групи.
12. Сформулювати означення кільця.
13. Яке кільце називають асоціативним (комутативним, асоціативно-комутативним, кільцем з одиницею)?
14. Яке кільце називають числовим?
15. Які умови досить перевірити, для того, щоб деяка числова множина була числовим кільцем?
16. Сформулювати означення дільників нуля в кільці.
17. Яке кільце називають кільцем з одиницею? Сформулювати означення дільників одиниці в такому кільці.
18. Сформулювати означення поля.
19. Яке поле називають числовим? Які умови досить перевірити, для того, щоб деяка числова множина була числовим полем?
Завдання:
1.
Вивчити
основні властивості (алгебраїчність,
асоціативність, комутативність, існування
нейтрального елемента, наявність
оборотних елементів) дії
 над елементами множини
над елементами множини
 ,
якщо:
,
якщо:
|
№ варіанта |
|
|
№ варіанта |
|
|
|
1 |
|
|
4 |
|
|
|
2 |
|
|
5 |
|
|
|
3 |
|
|
6 |
|
|
2.
Яку алгебраїчну структуру (групоїд,
напівгрупу, моноїд чи групу) утворює
множина, задана у прикладі 1, щодо вказаної
дії
 ?
?
3. Перевірити, чи буде групою задана множина щодо вказаної дії. Чи буде задана дія комутативною, якщо:
|
№ варіанта |
|
|
1 |
Множина всіх самосуміщень правильного многокутника відносно дії послідовного виконання перетворень. |
|
2 |
Множина
|
|
3 |
Множина
|
|
4 |
Множина
|
|
5 |
Множина
|
4.
Знайти порядок елемента
 групи
групи
 .
Побудувати циклічну групу, породжену
цим елементом та виписати усі її підгрупи:
.
Побудувати циклічну групу, породжену
цим елементом та виписати усі її підгрупи:
|
№ варіанта |
Елемент |
Група |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
5.
Перевірити, чи утворює кільце щодо
звичайних дій додавання та множення
чисел множина
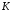 .
Якщо відповідь позитивна, то з’ясувати,
чи є це кільце полем.
.
Якщо відповідь позитивна, то з’ясувати,
чи є це кільце полем.
|
№ варіанта |
Множина |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
6.
Перевірити, чи утворює кільце множина
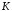 .
Чи є це кільце полем?
.
Чи є це кільце полем?
|
№ варіанта |
|
|
1 |
Множина
|
|
2 |
Множина
|
|
3 |
Множина
|
|
4 |
Множина
|
|
5 |
Множина
|


 ,
,


 ,
,





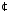







 відносно дії множення
своїх елементів.
відносно дії множення
своїх елементів. парних цілих чисел відносно дії
додавання.
парних цілих чисел відносно дії
додавання.
 всіх підстановок
всіх підстановок
 -го
степеня (
-го
степеня ( )
відносно дії множення
підстановок.
)
відносно дії множення
підстановок.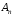 всіх парних підстановок
всіх парних підстановок
 -го
степеня (
-го
степеня ( )
відносно дії множення підстановок.
)
відносно дії множення підстановок.
 – мультиплікативна
група підстановок шостого
степеня.
– мультиплікативна
група підстановок шостого
степеня.
 – мультиплікативна
група коренів десятого степеня з
одиниці.
– мультиплікативна
група коренів десятого степеня з
одиниці.
 – мультиплікативна
група невироджених матриць другого
порядку з комплексними елементами.
– мультиплікативна
група невироджених матриць другого
порядку з комплексними елементами.
 – мультиплікативна
група коренів восьмого степеня
з одиниці.
– мультиплікативна
група коренів восьмого степеня
з одиниці.
 – група
функцій відносно дії суперпозиції
функцій.
– група
функцій відносно дії суперпозиції
функцій.
 .
. –– цілі
числа, кратні
–– цілі
числа, кратні
 (
( ,
,
 ).
).
 .
. відносно звичайних дій додавання та
множення матриць.
відносно звичайних дій додавання та
множення матриць. матриць другого порядку з цілими
елементами відносно звичайних дій
додавання та множення матриць.
матриць другого порядку з цілими
елементами відносно звичайних дій
додавання та множення матриць. матриць другого порядку з раціональними
елементами відносно звичайних дій
додавання та множення матриць.
матриць другого порядку з раціональними
елементами відносно звичайних дій
додавання та множення матриць. векторів простору щодо дій додавання
та векторного множення векторів.
векторів простору щодо дій додавання
та векторного множення векторів. цілочисельних векторів простору щодо
дій додавання та векторного множення
векторів.
цілочисельних векторів простору щодо
дій додавання та векторного множення
векторів.