Algebra_i_geometriya / ІІ модуль / NE_2.3 / Завдання для самостійної роботи до НЕ 2

Завдання для самостійної роботи студентів:

1. Знайти нормальний вигляд та перетворення, яке приводить до цього вигляду для квадратичної форми .

2. Знайти нормальний вигляд та перетворення, яке приводить до цього вигляду для квадратичної форми .

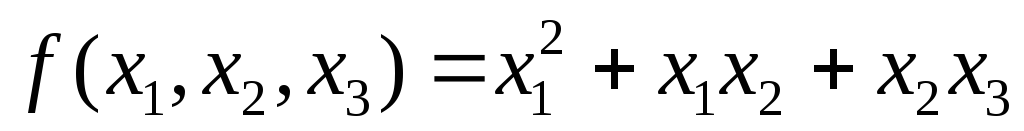3. Знайти ранг, додатний та від’ємний індекси інерції, сигнатуру квадратичної форми:

а) ;

б) ;

в) .

4. Методом Лагранжа звести квадратичну форму до канонічного (нормального) вигляду. Виписати лінійне невироджене перетворення, яке приводить цю форму до канонічного (нормального) вигляду. Чому дорівнює сигнатура форми?

5. Знайти канонічний вигляд квадратичної форми . Чи є ця форма додатно-визначеною?

6. Знайти нормальний вигляд та перетворення, яке приводить до цього вигляду для квадратичної форми:

а) ;

б) .

7. Знайти всі значення параметра , при яких квадратична форма

є додатно-визначеною.

8. З’ясувати, при якому значенні дійсна квадратична форма

розпадається на добуток дійсних лінійних форм.

9. Чи є еквівалентними квадратичні форми та над полем дійсних чисел?