Algebra_i_geometriya / ІІ модуль / NE_2.1 / Практичні заняття до НЕ 2

Приклади розв’язування задач

Приклад 1. За допомогою алгоритму Евкліда обчислити найбільший спільний дільник многочленів

та .

Розв. f:g

g:r₁

r₁:r₂

НСД

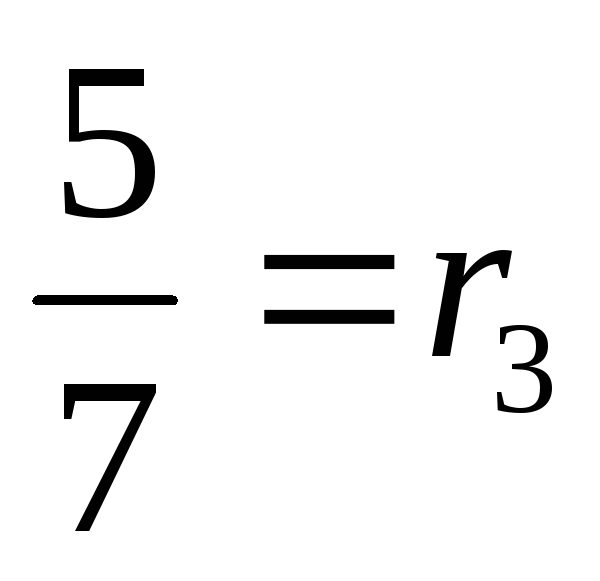
r₂:r₃

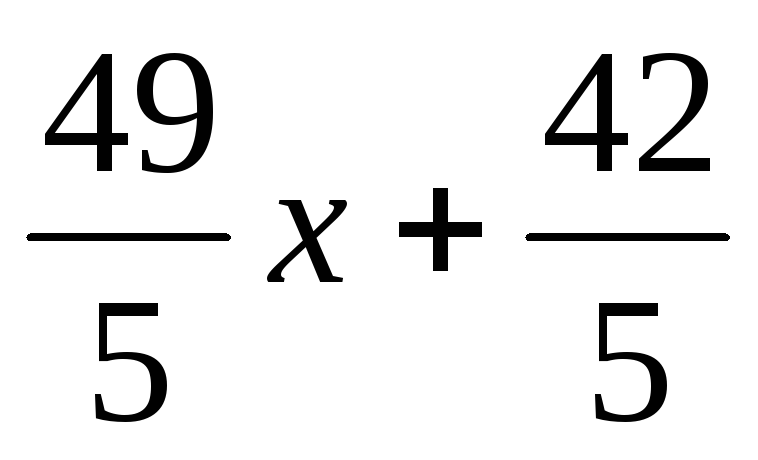
0

Отже, НСД

Приклад 2. Знайти НСД многочленів

та

Розв.

НСД

Приклад 3. Для многочленів

та

Побудувати многочлени та , які задовольняють рівність

де , використовуючи:

а) алгоритм Евкліда;

б) метод невизначених коефіцієнтів.

Розв. а) u, v за допомогою алгоритму Евкліда

f:g

g:r₁

r₁:r₂

0

Отже, НСД .

Розпишемо алгоритм Евкліда:

, де .

Звідси

Отже,

.

Відповідь:

.

б) Знайдемо тепер множини та методом невизначених коефіцієнтів.

Для цього скористаємося умовами:

‑ многочлени не вище 3-го степеня.

Отже,

де a, b, c, d, m, n, q, p ‑ ? шукані.

Складемо систему для знаходження цих коефіцієнтів. Для цього скористаємося умовою (*) та знайденим вище .

Маємо

Порівняємо коефіцієнти біля відповідних степенів змінної х:

Розв’язуємо отриману систему:

Із 1-го р-ня:

Із 8-го р-ня:

Із 2-го р-ня:

Із 3-го р-ня:

Із 4-го р-ня:

Враховуючи (3), маємо:

Із 5-го р-ня:

Із 6-го рівняння:

Із 7-го рівняння:

Розв’яжемо тепер систему рівнянь (3)-(8) відповідно до змінних a, b, c,d, m, n, q, p методом Гаусса:

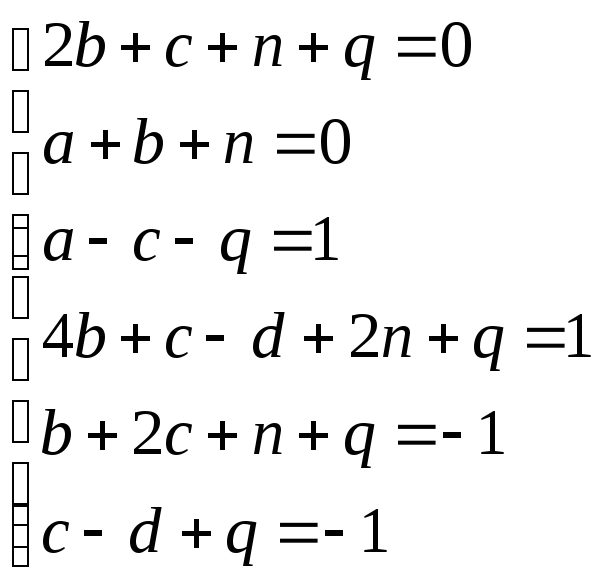
a b c d n q

Із (1) і (2) маємо, що

Отже

‑ шукані многочлени.

Відповідь:

а)

б)

Приклад 4. Розділити многочлени з остачею () та обчислити значення , якщо

а) б)

Користуємося схемою Горнера:

а)

	2	0	-5	0	-8	0
-3	2	-6	13	-39	109	-327

Отже,

та

б)

	2	0	-5	0	-8	0
1+і	2	2+2і	4і-5	-9-і	-16-10і	-6-26і

Отже, та

Приклад 5. Знайти значення многочлена

при:

а) б) .

Розв. Користуємося схемою Горнера:

	3	-2і	1	1-і	-2і
-1	3	-3-2і	4+2і	-3-3і	3+і
1+і	3	3-8і	-12-12і	-35+11і	-13+79і

Відповідь: а) б)

Приклад 6. Користуючись схемою Горнера, розкласти за степенями (х+1) многочлен.

Розв.

	1	2	-3	-4	1
-1	1	1	-4	0	1
-1	1	0	-5	5
-1	1	-1	-4
-1	1	-2
-1	1

Приклад 7. Виписати значення многочлена

та всіх його похідних при

	1	0	-4	6	-8	10
2	1	2	0	6	4	18
2	1	4	8	22	48
2	1	6	20	62
2	1	8	36
2	1	10
2	1

Отже,

Приклад 8. Знайти значення для коефіцієнта так, щоб

мав число коренем не нижче другої кратності.

Для того, щоб був коренем не нижче ІІ-ої кратності потрібно, щоб

.

Скористаємося схемою Горнера

	1	0	0			1
-1	1	-1	1	-1	1	0
-1	1	-2	3	-4

Звідси маємо, що .

Відповідь:

Приклад 9. Чому дорівнює кратність кореня для многочлена

?

Розв.

	3	2	1	0	-10	-8
-1	3	-1	2	-2	-8	0
-1	3	-4	6	-8	0
-1	3	-7	13	-21

Отже, корінь є другої кратності.

Приклад 10. Розкласти на суму простіших дробів І і ІІ типу дріб

.

Звідси, прирівнюючи чисельники (бо знаменники однакові) маємо:

Отже, .