spz / spz

ідентифікатора! Іншим недоліком є необхідність роботи з динамічним виділенням пам'ятідля побудови дерева..

Якщо припустити, що послідовність ідентифікаторів у вихідній програмі є статистично неупорядкованою (що в цілому відповідає дійсності), то можна вважати, що побудоване бінарне дерево буде невиродженим. Тоді середній час на заповнення дерева (Т3) і на пошук елемента в ньому (Тn) можна оцінити в такий спосіб :

Тз =N*O(log2 N).

Тn =O(log2 N).

У цілому метод бінарного дерева є досить удалим механізмом для організації таблиць ідентифікаторів. Він знайшов своє застосування в ряді компіляторів. Іноді компілятори будують кілька різних дерев ідентифікаторів різних типів і різної довжини .

Хеш-функції і хеш-адресація

1.Принципи роботи хеш-функцій.

2.Побудова таблиць ідентифікаторів на основі хеш-функцій.

3.Побудова таблиць ідентифікаторів методом ланцюжка.

4.Комбіновані способи побудови таблиць ідентифікаторів.

Логарифмічна залежність часу пошуку і часу заповнення таблиці ідентифікаторів — це самий добрий результат, якого можна досягти за рахунок застосування різних методів організації таблиць. Однак у реальних вхідних програмах кількість ідентифікаторів настільки велика, що навіть логарифмічну залежність часу пошуку від їхнього числа не можна визнати задовільною. Необхідні більш ефективні методи пошуку інформації в таблиці ідентифікаторів.

Кращих результатів можна досягти, якщо застосувати методи, зв'язані з використанням хеш-функцій і хеш-адресаціи.

Хеш-функціей F називається деяке відображення множини вхідних елементів R на множину цілих невід’ємних чисел Z: F(r) = n, r R, n Z. Сам термін «Хеш-функція» походить від англійського терміна «hash function» (hash

— «заважати», «змішувати», «плутати»). Замість терміна «хешування» іноді використовуються терміни «рандомізація», «перевпорядкування».

Множина припустимих вхідних елементів R називається областю визначення хеш-функції. Множиною значень хеш-функції F називається підмножина М з множини цілих невід’ємних чисел Z: M Z (M є підмножиною Z, М вкючене в Z), що містить усі можливі значення, які повертаються функцією F:

r R: F(r) М (Для всіх r, які належ R; F(r) належ M. )

Процес відображення області визначення хеш-функції на безліч значень називається «хешуванням».

При роботі з таблицею ідентифікаторів хеш-функція повинна виконувати відображення імен ідентифікаторів на множину цілих невід’ємних чисел.

Областю визначення хеш-функціи буде множина усіх можливих імен ідентифікаторів.

Хеш-адресація полягає у використанні значення, що повертається хешфункцією, як адресу комірки з деякого масиву даних . Тоді розмір масиву даних повинний відповідати області значень використовуваної хеш-функціи. Отже, у реальному компіляторі область значень хеш-функціи ніяк не повинна перевищувати розмір доступного адресного простору комп'ютера.

Метод організації таблиць ідентифікаторів, заснований на використанні хеш-адресації, полягає в розміщенні кожного елемента таблиці в комірку, адреса якого повертає хеш-функція, обчислена для цього елемента. Тоді в ідеальному випадку для розміщення будь-якого елемента в таблиці ідентифікаторів досить тільки обчислити його хеш-функцію і звернутися до потрібної комірки масиву даних. Для пошуку елемента в таблиці необхідно обчислити хеш-функцію для шуканого елемента і перевірити, чи не є задана

нею комірка масиву порожньою (якщо вона не порожня — елемент знайдений, якщо порожня — не знайдений).

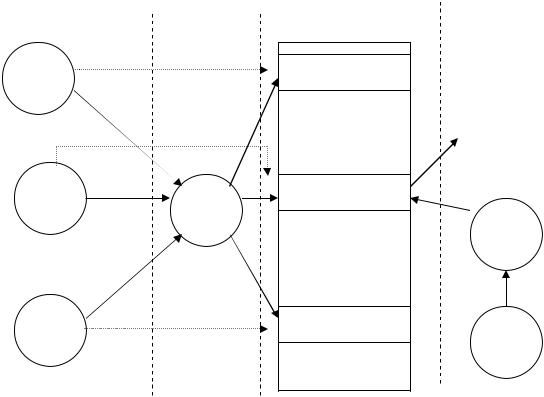
На мал. проілюстрований метод організації таблиць ідентифікаторів з використанням хеш-адресації. Трьом різним ідентифікаторам А1 А2, А3 відповідають на малюнку три значення хеш-функції n1, n2, n3. В комірки, адресовані n1, n2, n3, міститься інформація про ідентифікатори А1 ,А2, А3. При пошуку ідентифікатора А3 обчислюється значення адреси n3 і вибираються дані з відповідної комірки таблиці.

А2

А2

F

F

А3

А3

?

Рис. 13.3. Організація таблиці ідентифікаторів с використанням хеш-адресації

Цей метод дуже ефективний — як час розміщення елемента в таблиці, так і час його пошуку визначаються тільки часом, затрачуваним на обчислення хеш-функції, що у загальному випадку незрівнянно менше часу, необхідного на багаторазові порівняння елементів таблиці.

Метод має два очевидних недоліки. Перший з них – неефективне використання обсягу пам'яті під таблицю ідентифікаторів: розмір масиву для її збереження повинний відповідати області значень хеш-функції, у той час як реально збережених у таблиці ідентифікаторів може бути істотно менше. Другий недолік – необхідність відповідного розумного вибору хеш-функції.

Існують різні варіанти хеш-функцій. Одержання результату хеш-функції

— «хешування» — звичайно досягається за рахунок виконання над ланцюжком символів деяких простих арифметичних і логічних операцій. Найпростішою хеш-функціей для символу є код внутрішнього представлення в ЕОМ літери символу. Цю хеш-функцію можна використовувати і для ланцюжка символів, вибираючи перший символ у ланцюжку. Так, якщо двійкове ASCII представлення символу А є 00100001, то результатом хешування ідентифікатора АТаble буде код 00100001.

Хеш-функція, запропонована вище, очевидно не задовільна: при використанні такої хеш-функції виникне нова проблема — двом різним ідентифікаторам, що починаються з однієї і тієї ж букви, буде відповідати те саме значення хеш-функції. Тоді при хеш-адресації в одну комірку таблиці ідентифікаторів по тому самому адресі повинні бути поміщені два різних ідентифікатори, що є неможливим. Така ситуація, коли двом чи більш ідентифікаторам відповідає те саме значення функції називається колізією.

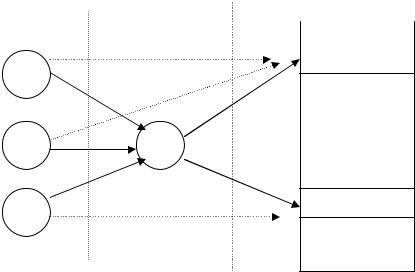
Виникнення колізії проілюстроване на мал. - двом різним ідентифікаторам A1 і

А2 F

А3

n3 А3

Рис. Виникнення колізії при використанні хеш-адресації

Природно, що хеш-функція, що допускає колізії, не може бути прямо використана для хеш-адресації в таблиці ідентифікаторів. Причому досить одержати хоча б один випадок колізії на всій множині ідентифікаторів, щоб такою хеш-функцією не можна було користуватися безпосередньо. Але в прикладі взята сама елементарна хеш-функція. А чи можливо побудувати нетривіальну хеш-функцію, яка б цілком виключала виникнення колізій?

Очевидно, що для повного виключення колізій хеш-функція повинна бути взаємно однозначної: кожному елементу з області визначення хешфункції повинне відповідати одне значення з її множини значень, але і кожному значенню з множини значень цієї функції повинний відповідати тільки один елемент з області її визначення. Тоді будь-яким двом довільним елементам з області визначення хеш-функції будуть завжди відповідати два різні її

значення. Теоретично для ідентифікаторів таку хеш-функцію побудувати можна, тому що й область визначення хеш-функції (усі можливі імена ідентифікаторів), і область її значень (цілі невід’ємні числа) є нескінченними перелічуваними множинами. Теоретично можна організувати взаємно однозначне відображення однієї перелічуваної множини на інше, але практично це зробити винятково важко1 .

Практично існує обмеження, що робить створення взаємно однозначної хеш-функції для ідентифікаторів неможливим. Справа в тому, що в реальності область значень будь-якої хеш-функції обмежена розміром доступного адресного простору в даній архітектурі комп'ютера. При організації хешадресації значення, використовуване як адреса таблиці ідентифікаторів не може виходити за межі, задані адресною сіткою комп'ютера2. Множина адрес будьякого комп'ютера з традиційною архітектурою може бути великою, але завжди кінцева, то обмежена. Організувати взаємно однозначне відображення нескінченної множини на кінцеве навіть теоретично неможливо. Можна врахувати, що довжина прийнятої до уваги рядка ідентифікатора і реальних компіляторів також практично обмежена — звичайно вона лежить у межах від 32 до 128 символів (то й область визначення хеш-функції кінцева). Але і тоді кількість елементів у кінцевій множині, що складає область визначення функції, буде перевищувати їхню кількість у кінцевій множині області значень функції (кількість усіх можливих ідентифікаторів все одно більше кількості припустимих адрес у сучасних комп'ютерах). Таким чином, створити взаємно однозначну хеш-функцію практично ні в якому варіанті неможливо. Отже, неможливо уникнути виникнення колізій.

Поки для двох різних елементів результати хешування різні, час пошуку збігається з часом, витраченим на хешування. Однак виникає утруднення, коли результати хешування двох різних елементів збігаються.

Для рішення проблеми колізії можна використовувати багато способів. Одним з них є метод «рехешування» (або «розміщення»). Відповідно до цього методу, якщо для елемента А адреса h(А), обчислена за допомогою хеш-функції вказує на уже зайняту комірку, то необхідно обчислити значення функції n1=h1(А) і перевірити зайнятість комірки за адресою n1. Якщо і вона зайнята, то обчислюється значення h2(A), і так доти, поки або не буде знайдений вільна комірка, або чергове значення hi(А) співпаде з h(А). В останньому випадку вважається, що таблиця ідентифікаторів заповнена і місця в ній більше немає - видається інформація про помилку розміщення ідентифікатора в таблиці. Особливістю методу є те, що спочатку таблиця ідентифікаторів повинна бути заповнена інформацією, що дозволила б говорити про те, що всі її комірки є порожніми (не містять даних). Наприклад, якщо використовуються покажчики

1 Элементарным примером такого отображения для строки символов является сопоставление ей двоичного числа, полученного путем конкатенации кодов символов, входящих в строку. Фактически сама строка тогда будет выступать адресом при хэш-адрсации Практическая ценность такого отображения весьма сомнительна.

2 Можно, конечно, организовать адресацию с использованием внешних накопителей для организации виртуальной памяти, но накладные затраты для такой адресации будут весьма велики; кроме того, компилятор не должен брать на себя функции ОС . Но даже в таком варианте адресное пространство никогда не будет бесконечным

для збереження імен ідентифікаторів, то таблицю треба попередньо заповнити порожніми покажчиками.

Таку таблицю ідентифікаторів можна організувати по наступному алгоритму розміщення елемента.

Крок 1. Обчислити значення хеш-функції n=h(A) для нового елемента А..

Крок 2. Якщо комірка за адресою n порожня, то помістити в неї елемент А і завершити алгоритм, інакше i:=l і перейти до кроку 3.

Крок 3. Обчислити ni=hi(А). Якщо комірка за адресою ni порожня, то помістити в неї, елемент А і завершити алгоритм, інакше перейти до кроку 4.

Крок 4. Якщо n=ni, то повідомити про помилку і завершити алгоритм, інакше і:=і+1 і повернутися до кроку 3.

Тоді пошук елемента А в таблиці ідентифікаторів, організованої таким чином, буде виконуватися по наступному алгоритму.

Крок 1. Обчислити значення хеш-функції n = h(A) для нового елемента А.

Крок 2. Якщо комірка за адресою n порожня, то елемент не знайдений, алгоритм завершений, інакше порівняти ім'я елемента в комірці n з ім'ям шуканого елемента А. Якщо вони збігаються, то елемент знайдений і алгоритм завершений, інакше і:=1 і перейти до кроку 3.

Крок 3. Обчислити ni=hi(А). Якщо комірка за адресою ni порожня чи n=ni , то елемент не знайдений і алгоритм завершений, інакше порівняти ім'я елемента в комірці ni з ім'ям шуканого елемента А. Якщо вони збігаються, то елемент знайдений і алгоритм завершений, інакше і:=і+1 і повторити крок 3.

Алгоритми розміщення і пошуку елемента схожі по виконуваних операціях. Тому вони будуть збігатися і по оцінках часу, необхідного для їхнього виконання.

При такій організації таблиць ідентифікаторів у випадку виникнення колізії алгоритм розміщає елементи в порожніх комірках таблиці, вибираючи їх певним чином. При цьому елементи можуть попадати в комірки з адресами, що потом будуть збігатися зі значеннями хеш-функції, що приведе до виникнення нових, додаткових колізій. Таким чином, кількість операцій, необхідних для пошуку або розміщення в таблиці елемента, залежить від заповнювання таблиці. Дійсно, функції hi(A) повинні обчислюватися одноманітно на етапах розміщення і пошуку елемента. Питання тільки в тому, як організувати обчислення функцій hi (А).

Найпростішим методом обчислення функції hi(A) є її організація у вигляді

hi(A) = (h(A) + pi)mod Nm,

де pi — деяке ціле число, що обчислюється,

а Nm - максимальне число елементів у таблиці ідентифікаторів.

У свою чергу, найпростішим підходом тут буде покласти Рi = і. Тоді одержуємо формулу

hi(A)=(h(A)+i) modNm.

У цьому випадку при збіганні значень хеш-функції для яких-небудь елементів пошук вільної комірки в таблиці починається послідовно від поточної позиції, заданою хеш-функціею h(A).

Цей спосіб не можна визнати особливо вдалим — при співпаданні хеш- адрес елементи в таблиці починають групуватися навколо них, що збільшує число необхідних порівнянь при пошуку і розміщенні. Середній час пошуку елемента в такій таблиці в залежності від числа операцій порівняння можна оцінити в такий спосіб :

Тn= O((l-Lf/2)/(l- Lf)).

Тут Lf — (load factor) ступінь заповнювання таблиці ідентифікаторів - відношення числа зайнятих комірок таблиці до максимально припустимого числа елементів у ній: Lf = N/Nm.

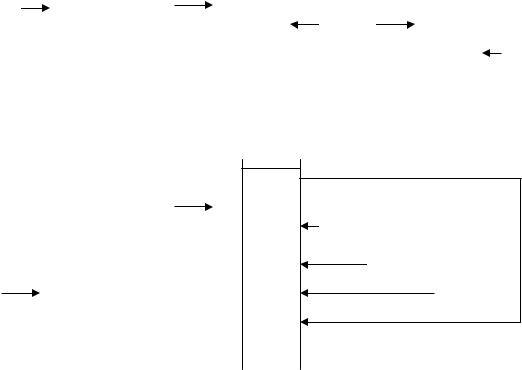
Розглянемо як приклад ряд послідовних комірок таблиці n1, n2, n3, n4, n5 і ряд ідентифікаторів, які треба розмістити в ній: А1, А2, А3, А4 ,А5 за умови, що h(A1) = h(A2) = h(A5) = n1, h(A3) = n2; h(A4) = n4. Послідовність розміщення ідентифікаторів у таблиці при використанні найпростішого методу рехешування показана на мал. 13.5. В результаті після розміщення в таблиці для пошуку ідентифікатора А1 буде потрібно 1 порівняння, для A2 - 2 порівняння, для А3 — 2 порівняння, для А4 — 1 порівняння і для А5 — 5 порівнянь.

Рис. 13.5. Заповнення таблиці ідентифікаторів при використанні найпростішого рехешування

Навіть такий примітивний метод рехешування є досить ефективним засобом організації таблиць ідентифікаторів при неповному заповненні таблиці. Маючи, наприклад, навіть заповнену на 90 % таблицю для 1024 ідентифікаторів, у середньому необхідно виконати 5,5 порівнянь для пошуку одного ідентифікатора, у той час як навіть логарифмічний пошук дає в середньому від 9 до 10 порівнянь. Порівняльна ефективність методу буде ще вище при рості числа ідентифікаторів і зниженні заповнювання таблиці.

Середній час на розміщення одного елемента в таблиці і на пошук елемента в таблиці можна знизити, якщо застосувати більш досконалий метод рехешування. Одним з таких методів є використання в якості рi для функції hi(A) = (h(A) + pi)mod Nm послідовності псевдовипадкових цілих чисел p1, p2 , … pk при гарному виборі генератора псевдовипадкових чисел довжина послідовності k буде k= N m . Тоді середній час пошуку одного елемента в таблиці можна оцінити в такий спосіб:

En=O((1/Lf)*log2(1-Lf))

Існують і інші методи організації функцій рехешуванні hi(A), засновані на квадратичних обчисленнях, наприклад, на обчисленні по формулі hi(A) = (h(A)*i) mod Nm, якщо Nm — просте число. У цілому рехешування дозволяє отримати непоганих результатів для ефективного пошуку елемента в таблиці (кращих, чим бінарний пошук і бінарне дерево), але ефективність методу сильно залежить від заповнювання таблиці ідентифікаторів і якості

використовуваної хеш-функції — чим рідше виникають колізії, тим вище ефективність методу. Вимога неповного заповнення таблиці веде до неефективного використання обсягу доступної пам'яті.

Побудова таблиць ідентифікаторів методом ланцюжків

доступного компілятору. Причому обсяг невикористовуваної пам'яті буде тим вище, чим більше інформації зберігається для кожного ідентифікатора. Цього недоліку можна уникнути, якщо доповнити таблицю ідентифікаторів деякою проміжною хеш-таблицею.

В комірках хеш-таблиці може зберігатися або порожнє значення, або значення покажчика на деяку область пам'яті з основної таблиці ідентифікаторів Тоді хеш-функція обчислює адресу, по якій відбувається звертання спочатку до хеш-таблиці, а потім уже через неї по знайденій адресі

— до самої таблиці ідентифікаторів. Якщо відповідна комірка таблиці ідентифікаторів порожня, то комірка хеш-таблиці буде містити порожнє значення. Тоді зовсім не обов'язково мати в самій таблиці ідентифікаторів комірку для кожного значення хеш-функції – таблицю можна зробити динамічною так, щоб її обсяг ріс у міру заповнення (спочатку таблиця идинтификаторів не містить ні одної комірки, а всі комірки хеш-таблиці мають порожнє значення).

Такий підхід дозволяє отримати два позитивних результатів: по-перше немає необхідності заповнювати порожніми значеннями таблицю ідентифікаторів - це можна зробити тільки для хеш-таблиці; по-друге, кожному ідентифікатору буде відповідати тільки одна комірка у таблиці ідентифікаторів ( у ній не буде порожніх невикористовуваних комірок). Порожні комірки в такому випадку будуть тільки в хеш-таблиці, і обсяг невикористовуваної пам'яті не буде залежати від обсягу інформації, збереженої для кожного ідентифікатора — для кожного значення хеш-функції буде витрачатися тільки пам'ять, необхідна для збереження одного покажчика на основну таблицю ідентифікаторів.

На основі цієї схеми можна реалізувати ще один спосіб організації таблиці ідентифікаторів за допомогою хеш-функцій, називаний «метод ланцюжків”. Для методу ланцюжків у таблицю ідентифікаторів для кожного елемента додається ще одне поле, у якому може міститися посилання на будьякий елемент таблиці. Спочатку це поле завжди порожнє (нікуди не вказує). Також для цього методу необхідно мати одну спеціальну змінну, котра завжди вказує на першу вільну комірку основної таблиці ідентифікаторів (спочатку — указує на початок таблиці).

Метод ланцюжків працює в такий спосіб по наступному алгоритму.

Крок 1. В усі комірки хеш-таблиці помістити порожнє значення, таблиця ідентифікаторів не повинна містити ні одної комірки, змінна FreePtr (покажчик першої вільної комірки) указує на початок таблиці ідентифікаторів; і:=1.

Крок 2. Обчислити значення хеш-функції ni; для нового елемента Аi;. Якщо комірка хеш-таблиці за адресою ni порожня, то помістити в неї значення змінної FreePtr і перейти до кроку 5; інакше — перейти до кроку 3.

Крок 3. Покласти j:=l, вибрати з хеш-таблиці адреса комірки таблиці ідентифікаторів mj і перейти до кроку 4.

Крок 4. Для комірки таблиці ідентифікаторів за адресою mj перевірити значння поля посилання. Якщо воно порожнє, то записати в нього адресу з перемінної FreePtr і перейти до кроку 5; інакше j:=j+l, вибрати з поля посилання адресу mj і повторити крок 4.

Крок 5. Додати в таблицю ідентифікаторів нову комірка, записати в неї інформацію для елемента Aі (поле посилання повинне бути порожнім), у змінну FreePtr помістити адресу за кінцем доданої комірки. Якщо більше немає ідентифікаторів, які треба розмістити в таблиці, то виконання алгоритму закінчене, інакше і:=і+1 і перейти до кроку 2.

Пошук елемента в таблиці ідентифікаторів, організованої в такий спосіб буде виконуватися по наступному алгоритму.

Крок 1. Обчислити значення хеш-функції n для шуканого елемента А. Якщо комірка хеш-таблиці за адресою n порожня, то елемент не знайдений і алгоритм завершений, інакше покласти j:=l, вибрати з хеш-таблиці адресу комірки таблиці ідентифікаторів mj=n.

Крок 2. Порівняти ім'я елемента в комірки таблиці ідентифікаторів за адресою mj з ім'ям елемента А. Якщо вони співпадають, то шуканий елемент знайдений і алгоритм завершений, інакше - перейти до кроку 3.

Крок 3. Перевірити значення поля посилання в комірці таблиці ідентифікаторів за адресою mj . Якщо воно порожнє, то шуканий елемент не знайдений і алгоритм завершений ; інакше j:=j+l, вибрати з поля посилання адреса mj і перейти до кроку 2.

При такій організації таблиць ідентифікаторів у випадку виникненні колізії алгоритм розміщає елементи в комірках таблиці, зв'язуючи їх один з одним послідовно через поле посилання. При цьому елементи не можуть попадати в комірки з адресами, що потім будуть співпадати зі значеннями хешфункції. Таким чином, додаткові колізії не виникають. У підсумку, у таблиці виникають своєрідні ланцюжки зв'язаних елементів, відкіля відбувається і назву даного методу — «метод ланцюжків».