1. Пограничний шар і турбулентність

При обтіканні тіла повітряним потоком шари повітря в безпосередній близкості від поверхні тіла завдяки в'зкості гальмуються, і в них виникають вихори. Ці вихори захоплюються загальним потоком, витягуються у невпорядковані хвости. Завихрений шар, що безпосередньо прилягає до тіла, яке обтікається, називається пограничним шаром або шаром поверхневого завихрення. В ньому швидкість рідини змінюється від нуля до швидкості незбуреного потоку, але чіткого поділу між пограничним шаром і зовнішнім потоком немає. Теоретично товщина цього шару змінюється по параболічному закону.

Далі рис.19 на стор. 46.

Характер туху рідини в пограничному шарі визначається безрозмірним параметром, який називається критерієм Рейнольдса і дорівнює

,

де ω - швидкість рідини, l – лінійний параметр, який характеризує розміри поверхні, ν – коефіцієнт кінематичної в’язкості.

Рідина при малих числах Rе в пограничному шарі має ламінарний характер (коли рідина рухається паралельними шарами, які не перемішуються), а при Rе>Rе_кр – турбулентний. Коефіцієнт опору у турбулентному шару більший, ніж у ламінарному. Але збільшення турбулентності збільшує коефіцієнт опору лише у тіл, у яких головною складовою опору є тертя, а не тиск. До таких тіл належать: пластина вздовж потоку, крила, дирижабль та інші тіла з хорошою формою обтікання.

При обдуванні тіл, в яких опір залежить, в основному, від тиску (куля, пластина, перпендикулярна потоку, дирижабль, поставлений поперек потоку), опір в турблентному потоці може вявитись меншим, ніж в ламінарному. При цьому зменшення величини коефіцієнту опору відбудеться одночасно з переходом пограничного шару із ламінарного в турбулентний.

2. Три системи координат в аеродинаміці

В елементарній аеродинаміці користуються трьома системами координат:

• Земною

• Поточною

• Зв’язаною

В земній системі координат одна із осей, зазвичай OY₀, спрямовується вертикально вверх, а дві інші – OX₀ і OZ₀ розміщуються в горизонтальній площині. Цією системою координат користуються при встановленні аеродинамічних труб і моделей в них.

В поточній системі координат ОХ направляється за вектором незбуреного потоку, OY – в площині симетрії моделі ( вона є віссю підйомної сили); OZ (бічна) розміщується перпендикулярно до OX і OY. Площини, які утворюються осями координат, називаються XY – площиною потоку, XZ – площиною ковзання, YZ – лобовою площиною.

При узгоджені потоків в аеродинамічних трубах, поточні осі приводять до спів падання із земними осями труби.

Початкові координати поточних осей для моделей літаків і дирижаблів вибирають в точках, де знаходяться центри тяжіння машини і для окремого (ізольованого) крила – біля його передньої кромки.

Осі координат, які вважаються під час дослідів жорстко з’єднаними з моделлю, називається зв’язаними. Початок цих осей координат поміщають в точки центри тяжіння натурального літака або в деякій умовній точці. Вісь , яка називається повздовжньою, розміщається в площині симетрії моделі; у літака паралельно центру хорди літака, у дирижабля – паралельно його осі. Вісь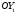називають нормальною віссю і розміщують в площині симетрії моделі перпендикулярно

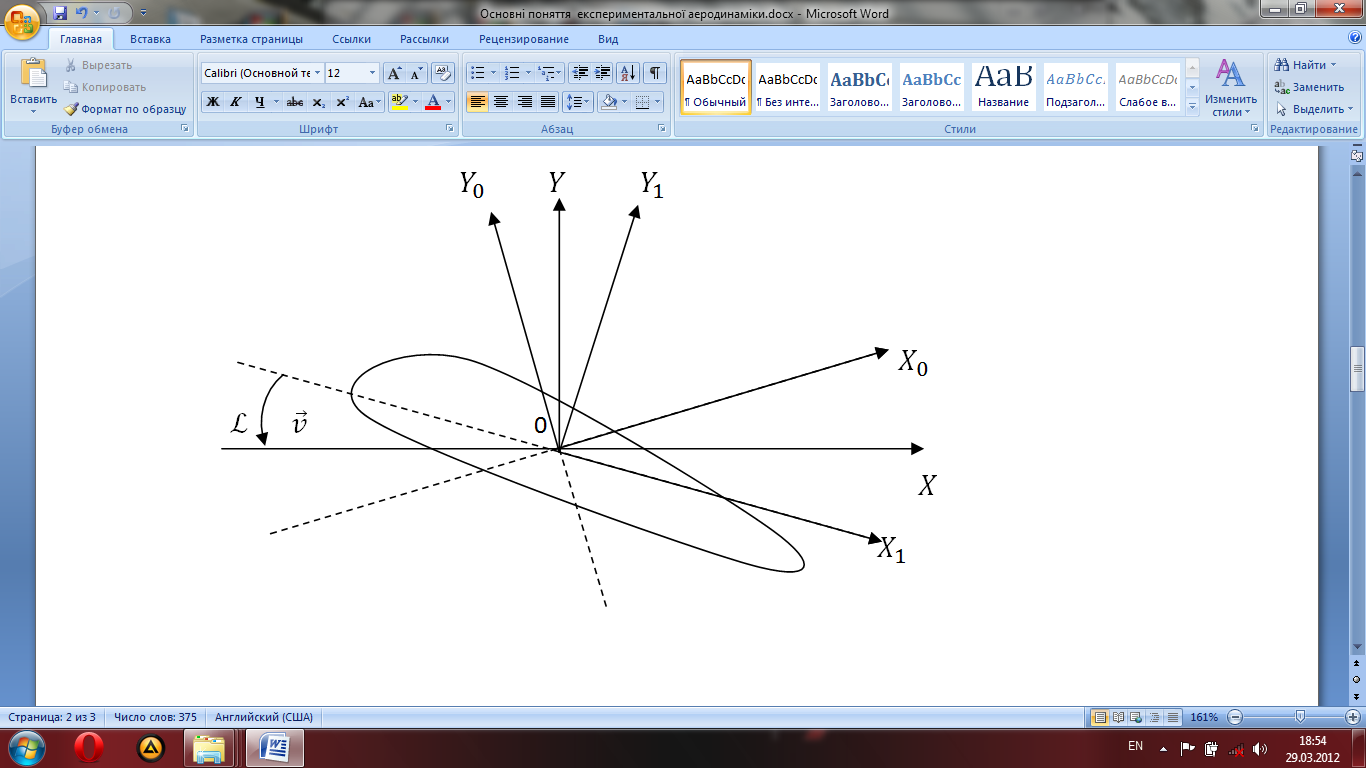
Вісь називають попереч-ною і направляють перпенди-кулярно осям і . Площина називається площиною симетрії, - головною площиною, а поперечною. Всі ці системи координат відносно моделі зображені на рисунку, де 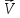– швидкість потоку, пунктирна пряма – напрямок хорди крила. При повертанні крила навколо осі OZ буде змінюватися кут між і площиною крила . Цей кут позначається α і називається істиннимкутом атаки.

При розв’язуванні практичних задач від моделі до зразка переходять за допомогою аеродинамічних коефіцієнтів. Для цього певну аеродинамічну силу R, яка діє на тіло, котре обтікається потоком і коефіцієнт , що їй відповідає, розкладають на компоненти по поточним вісям. Отримують:

Лобовий опір: X=C_хSq=C_хS, де С_х – коефіцієнт лобового опору; підйомну силу: Y=C_уSq=C_уS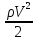, де С_у – коефіцієнт підйомної сили;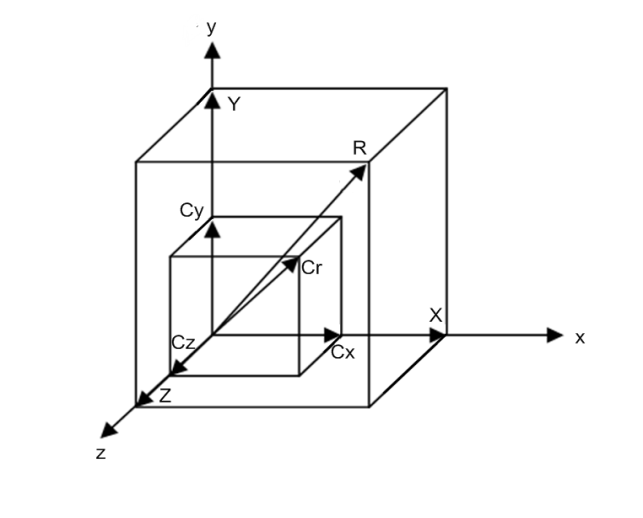

бічну силу : Z= C_zSq=C_zS , де

C_z – коефіцієнт бічної сили.

Із рис. бачимо, що сила R і коефіцієнт є рівнодійними відповідних компонент:

R= , =.

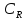Розкладаючи моменти по сям координат, отримаємо і відповідні моменти:

M_і=C_miSqL=C_mі SL,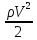

де і=x,y,z, S- площа крил або інша характерна площа тіла, L – умовна довжина.

Рівнодійний або повний момент: M=

І C_m =,

де C_mx , C_my ,C_mz - коефіцієнти моментів і є безрозмірними числами.

C_m називається коефіцієнтом повного аеродинамічного моменту. Отже, формула для аеродинамічного моменту така: M=C_m SL.

3. Поняття про аеродинамічні коефіцієнти. Перехід від моделі до зразка. Крива Лілієнталя

В результаті аеродинамічних досліджень обтікання тіл повітряним потоком в аеродинамічній трубі отримують такі аеродинамічні коефіцієнти:

Коефіцієнт сили опору: C_х =;

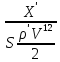Коефіцієнт підйомної сили: C_у =; ; Коефіцієнт бічної сили: С_z =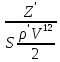, де- відповідні сили, що діють на зразок.

Існують і відповідні коефіцієнти для моментів.

Дія сили на тіло будь-якої форми визначають за допомогою рівняння:

P_х =C_хF∙.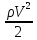

F – проекція площі тіла на площину, перпендикулярну напрямку повітряного потоку.

Криві, які характеризують аеродинамічні властивості крила взагалі, називаються аеродинамічними характеристиками. Крива, яка зображує залежність C_у від C_у, називається кривою або полярою Лілієнталя. Її побудова здійснюється так:

Із характеристик C_у=f(α) і C_ч =f(α) для кожного кута атаки беруть відповідні значення С_у і С_х, і наносять в прямокутну систему координат, надписуючи біля кожного точки величину α. Лінія від точки.0 – початку координат до будь-якої точки М на кривій Лілієнталя дає відрізок ОМ, який дорівнює 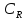- коефіцієнту рівнодійної суми підйомної сили і сили опору. Розмірні величини сил отримують із кивої Лілієнталя., помноживши її коефіцієнти на площуS реального зразка і швидкісний напір 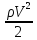, а саме:

X=C_хS , Y=C_уS , Z=C_zS .

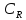Якістю крила К називається тангенс кута , який утворює вектор з віссю Ох: tg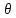==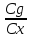K. Обернене відношення називається оберненою якістю крила: µ=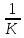=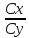. Якість найкращих сучасних літаків дорівнює 22.

Крива (поляра) Лілієнталя.

4. Теорема М.Е.Жуковського про підйомну силу крила

При обтіканні крила повітряним потоком, над крилом створюється понижений тиск, а під ним –підвищений. На основі теореми Бернуллі у випадку нестискуваних рідини це означає, що швидкість струменок, які течуть безпосередньо над крилом, буде більша, ніж швидкість далеко від крила, а під ним – менша. Якщо окреслити контур навколо крила, то на його ділянці над крилом течія швидкості буде більшою, ніж від’ємна течія під ним. Це вказує на те, що навколо крила, яке дає підйомну силу, існує циркуляція швидкості. А оскільки циркуляція швидкості існує і навколо вихрового шнура, то Жуковський запропонував замінювати при розрахунках крило пучком вихорів, які він назвав приєднаними вихорами. (Нагадаємо, що циркуляцією швидкості називається течія швидкості по замкненому контуру. Її розмірність м²/c.)

Жуковський так сформулював свою теорему:

підйомна сила, що діє на крило безмежного розмаху, дорівнює густині рідини, помноженій на циркуляцію, на швидкість потоку на безмежності і на довжину вибраного куска крила:

Y=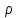VГl (1)

Y – сила, перпендикулярна швидкості незбуреного потоку, яка діє на відрізок крила довжиною l , - масова густина, Г- циркуляція швидкості.

Напрямок сили отримується поворотом вектора швидкості на прямий кут в сторону, обернену циркуляції.

При розв’язуванні практичних задач доводиться користуватися теоретичною формулою (1) і формулою експериментальної аеродинаміки:

Y=C_уS = C_у bl , (2)

де S - площа прямокутного крила з розмахом l і шириною b.

Прирівнюючи (1) і (2), отримаємо рівняння зв’язку:

Г=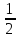Суb (3)

Тому, що воно пов’язує експериментальну величину С_у і теоретичну Г.

5.. Системи вітродвигунів

Рисунки 37 – 40 на стор.79-81.

Класифікація вітродвигунів за принципом їх роботи:

За схемою пристрою вітроколеса і його положенню відносно вітру системи вітродвигунів поділяються на три класи:

1.Вітродвигуни, в яких вітрове колесо розміщено у вертикальній площині, при цьому площина обертання перпендикулярна напрямку вітру, отже, вісь вітроколеса паралельна потоку. Це крильчаті вітродвигуни. Вони бувають ще багатолопатні і малолопатні. Крім того, в залежності від швидкохідності і типу вітроколеса крильчаті вітродвигуни поділяються ще на три групи:{Швидкохідністю називається відношення колової швидкості кінця лопаті до швидкості вітру }

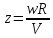1. вітродвигуни багатолопатні, тихохідні із z≤2.

2. вітродвигуни малолопатні, тихохідні (найпростішої деревометалічної конструкції), в тому числі вітряні млини із z>2.

3. вітродвигуни малолопатні, швидкохідні із z≥3.

2. До другого класу відносяться системи вітродвигунів з вертикальною віссю обертання вітрового колеса.

За конструкцією вони поділяються на: 1)карусельні, в яких неробочі лопаті або прикриваються ширмою, або розміщуються ребром проти вітру; 2)роторні вітродвигуни системи Савоніуса.

3. Барабанні вітродвигуни, які працюють за принципом водяного млина. У них вісь обертання горизонтальна і перпендикулярна напрямку вітру.

6. Робота поверхні при дії на неї сил вітру

Потік вітру з поперечним перерізом F володіє кінетичною енергією . Маса повітря, що протікає через перерізF зі швидкістю V, дорівнює m=ρFV. Підставивши цю величину, отримаємо (1).

Отже, енергія вітру змінюється пропорційно кубу його швидкості.

Знайдемо, яку частку енергії вітру може перетворити в корисну роботу поверхня, поставлена перпендикулярно до напрямку вітру і яка рухається в тому ж напрямку (вітродвигун карусельного типу).

Потужність або секундна робота Т є добутком сили Р на швидкість V: T=PV (2).

Одну і ту ж роботу можна отримати або за рахунок великої сили при малій швидкості переміщення, або, навпаки, за рахунок малої сили, і, відповідно, малої поверхні, але при великій швидкості її переміщення.

Рис.41 на стор.82

Нехай маємо поверхню F, перпендикулярну швидкості вітру. Повітряний потік створить тиск силою Р_х на поверхню, внаслідок чого вона буде переміщуватись в напрямку потоку зі швидкістю U, і виконуватиметься робота T=P_xU, де P_x-сила опору яка дорівнює

P_x=C_xF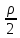 (V-U)², (3)

тому що в даному випадку вітер набігає на поверхню з відносною швидкістю W=V-U.

В результаті отримаємо:

Т= C_xF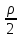 (V-U)² U (4)

Знайдемо відношення (4)до(1). Отримаємо коефіцієнт використання енергії вітру:

ξ =(V-U)^2,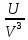

Після деяких перетворень

ξ=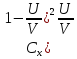 (5)

Нескладні розрахунки показують, що для отримання максимального ξ, поверхня повинна переміщуватись зі швидкістю U=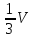(6)i ξ=0.148C_x. Коефіцієнт лобового опору C_x для поверхонь, розміщених перпендикулярно до потоку вітру, дорівнює 1.3, отже ξ=0,148*1,3=0,192. Тобто максимальний коефіцієнт використання енергії вітру при роботі поверхні силою опору не може бути більшим, ніж ξ=0,192.