
Chasovim_2M_1
.pdf
1.Амплитудная импульсная модуляция (АИМ)
2.Широтная импульсная модуляция (ШИМ)
3.Временная импульсная модуляция (ВИМ)
4. Обзор методов расчета частотных спектров импульсно-модулированных сигналов 5. Нестатистические методы расчета частотных спектров модулированных последовательностей импульсов 6. Понятие о статистических методах расчета частотных спектров
7. Частотные спектры и способы демодуляции импульсных сигналов
2.Амплитудная импульсная модуляци.
3.Широтная импульсная модуляция
8. Модуляционные в демодуляционные искажения в системах с ВРК
§ 5.1. Основные виды импульсной модуляции и способы их получения
1. Амплитудная импульсная модуляция (АИМ)
Амплитудно-модулированная последовательность импульсов оп-ределяется соотношением (3.103), если амплитуда импульсов U(t) изменяется в соответствии с передаваемым сообщением, а все ос-тальные параметры сохраняются неизменными, т. е.
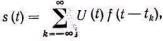 (5.1)
(5.1)
где
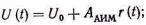 ' (5.2)
' (5.2)
U0—амплитуда немодулированных импульсов (рис.5.1); ААИМ — постоянный коэффициент, определяющий крутизну модуляционной характеристики; r(t)=rмаксD(t) — модулирующее на-пряжение (передаваемое сообщение), определяемое выражениями (4.9) и (4.11). Амплитуда импульсов (5.2)
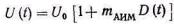 (5.3)
(5.3)
где
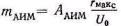 (5.4)
(5.4)
— коэффициент амплитудной импульсной модуляции.
Если учесть формулу (4.9), определяющую нормированную функ-цию сообщения D(t), то после подстановки равенства (5.3) в со-отношение (5.1), получим
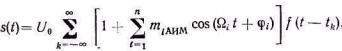 (5.5)
(5.5)
где
 (5.6)
(5.6)
— парциальный коэффициент модуляции [см. формулу (4.17)].
Различают амплитудную импульсную модуляцию первого рода (АИМ-1) и модуляцию второго рода
(АИМ-2).
Рис. 5.1
При АИМ-1 амплитуда импульса следует за изменениями мо-дулирующей функции в течение всего времени существования это-го импульса (рис. 5.1б). Модулированная последовательность в этом случае определяется .следующим выражением:
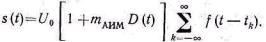 (5.7)
(5.7)
Амплитуда импульсов U(t) определяется формулой (5.3) и может быть вынесена за знак суммы, поскольку она не зависит от k.
В случае АИМ-2 амплитудная модуляция импульсов опреде-ляется мгновенными значениями функции сообщения, взятыми в моменты tk=kTп. Поэтому амплитуда импульсов здесь пропорцио-нальна D(tk) и сохраняется постоянной во время импульса (рис. 5.1г). Модулированный сигнал в этом случае можно запи-сать в следующем виде:
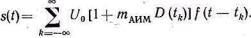 (5.8)
(5.8)
Если длительность импульсов т<Гп, то различие между АИМ-1 и АИМ-2 становится несущественным. Анализ показывает, что АИМ-2 сопровождается искаже-ниями и на передающей стороне этот вид модуляции обычно не применяется. АИМ-2 получается на приемной стороне, если перед демодуляцией АИМ-1 осуществ-ляется удлинение импульсов. Выбор параметров модуляции и тре-бования к характеристикам модулятора устанавливаются на ос-нове анализа модуляционных и демодуляционных искажений, ко-торый
последует далее.
2. Широтная импульсная модуляция (ШИМ)
Параметр модуляции при ШИМ—длительность импульсов т— не входит явно в формулу (3.103), и поэтому для аналитической запи-си ШИМ представим периодическую последовательность импуль-сов в следующей форме:
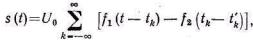 (5.9)
(5.9)
где f1(t-tk), f2(t-t`k) —функции, описывающие закон изменения переднего и заднего фронтов импульсов соответственно.
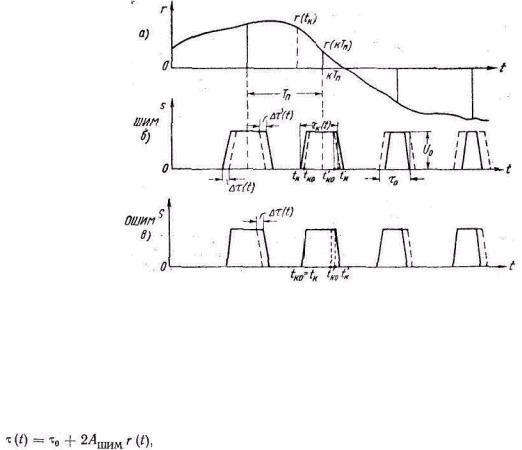
При отсутствии модуляции моменты появления переднего и заднего фронтов (рис. 5.4)
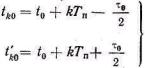 (5.10)
(5.10)
Длительность модулированных импульсов определяется из рис. 5.46 следующим образом:
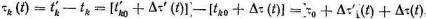 (5.11)
(5.11)
где t , t - мгновенные отклонения переднего и заднего фронтов при модуляции.
Рис. 5.4
Различают два вида модуляции импульсов по ширине (рис. 5.46 и в): двустороннюю (ШИМ) и одностороннюю широтные модуля-ции (ОШИМ). Широтная модуляция называется двусторонней симметричной, если оба фронта импульсов сдвигаются на одина-ковые временные интервалы, в противном случае ее называют двусторонней несимметричной.
Для симметричной ШИМ 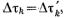 , и поэтому из выражения (5.11) получается
, и поэтому из выражения (5.11) получается
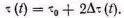 (5.12)
(5.12)
Изменения длительности импульсов вызываются модулирую-щим напряжением r(t), поэтому последнее соотношение можно представить в следующей форме:
где Ашим[мксек/В] - крутизна характеристики модулятора ШИМ.
Принимая во внимание выражение (4.11), для t получаем
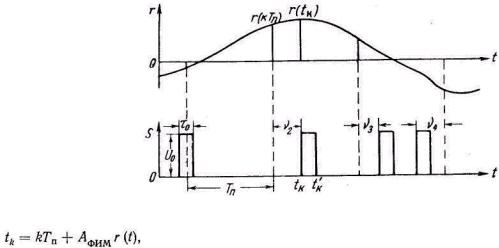
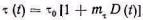 (5.13)
(5.13)
Здесь
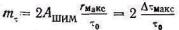 (5.14)
(5.14)
- коэффициент широтной 'модуляции импульсов;
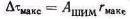 (5.15)
(5.15)
- максимальное отклонение фронта импульсов в одну сторону.
Односторонняя широтная модуляция (ОШИМ) определяется аналогично выражению (5.13), при этом числитель в соотношении (5.14) будет в два раза меньше. Поскольку всегда должно выпол-няться условие
 при ШИМ и условие
при ШИМ и условие 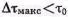 при ОШИМ, коэффициент широтной модуляции m в первом
при ОШИМ, коэффициент широтной модуляции m в первом
иво втором случаях должен удовлетворять требованию m <1.
Взависимости от того, каким образом устанавливается связь между моментом отсчета мгновенных значений модулирующей функции r(t) и шириной импульса, различают широтную импульс-ную модуляцию первого рода (ШИМ-1) и второго рода (ШИМ-2).
Вслучае ШИМ-1 длительность импульсов определяется зна-чениями модулирующей функции r(t) в моменты возникновения переднего или заднего фронта импульсов (рис. 5.4), т. e.
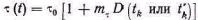 (5.16)
(5.16)
При ШИМ-2 длительность импульсов пропорциональна мгно-венным значениям модулирующего напряжения в тактовых точ-ках, т. e.
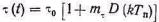 (5.17)
(5.17)
Обычно применяется ОШИМ-1. При 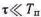 различие между ШИМ-1 и ШИМ-2 несущественно. Широтную импульсную модуляцию можно получить несколькими способами. В частности, Для этой цели используются схемы, действие которых основано на сравнении пилообразного напряжения с модулирующим r(t), релак-сационные схемы, например запертый мультивибратор, фантастрон и т.п. схе-мы с использованием ферриттранзисторных элементов.
различие между ШИМ-1 и ШИМ-2 несущественно. Широтную импульсную модуляцию можно получить несколькими способами. В частности, Для этой цели используются схемы, действие которых основано на сравнении пилообразного напряжения с модулирующим r(t), релак-сационные схемы, например запертый мультивибратор, фантастрон и т.п. схе-мы с использованием ферриттранзисторных элементов.
3. Временная импульсная модуляция (ВИМ)
При временной импульсной модуляции сдвиг импульсов k t относительно тактовых точек kTп изменяется по закону r(t), отображающему передаваемую информацию (рис. 5.7). Последова-тельность импульсов, модулированных по положению, можно по-лучить из выражения (5.9), если принять, что разность моментов возникновения переднего и заднего фронтов постоянна и равна длительности импульсов , поэтому для ВИМ
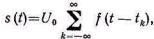 (5.20)
(5.20)
где
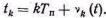 (5.20а).
(5.20а).
В зависимости от закона изменения tk различают два вида временной импульсной модуляции: фазовую импульсную модуляцию (ФИМ) и частотную импульсную модуляцию (ЧИМ). Различие между ФИМ и ЧИМ такое же, как и между ФМ и ЧМ (гл. 4). Остановимся сначала на рассмотрении фазовой импульсной модуляции.
Рис. 5.7
Уравнение, определяющее Моменты возникновения канальных импульсов, в обозначениях рис. 5.7 будет

где 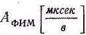 — крутизна характеристики модулятора ФИМ.
— крутизна характеристики модулятора ФИМ.
Подставляя в последнее выражение r(t) через нормированную функцию сообщения D(t) формулы (4.11), получаем
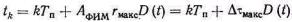 (5.21)
(5.21)
Здесь 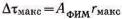 — максимальная девиация импульсов.
— максимальная девиация импульсов.
Если моменты возникновения импульсов подчиняются законо-мерности (5.21), то получаем фазовую импульсную модуляцию. Существует несколько разновидностей ФИМ, в частности фазовая импульсная модуляция первого рода (ФИМ-1) и второго рода (ФИМ-2).
ПРИ ФИМ-1 моменты возникновения импульсов
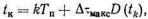 (5-22)
(5-22)
т. е. временной сдвиг импульса k t пропорционален значению модулирующей функции D(t) в момент
появления этого же импульса tk (рис. 5.7).
Моменты возникновения импульсов при ФИМ-2
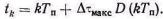 (5.23)
(5.23)
В данном случае временной сдвиг импульсов пропорционален значениям модулирующего напряжения в тактовых точках. Различие между ФИМ-1 и ФИМ-2 становится несущественным, если выполнено условие
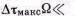 1, где Q — частота модулирующего напряжения.
1, где Q — частота модулирующего напряжения.
Фазовую импульсную модуляцию можно получить из широтной, если последовательность модулированных по ширине импульсов продифференцировать и исключить из последовательности импульсы, соответствующие неподвижно-му фронту. Нетрудно убедиться, что при таком способе получения фазоимпульсной модуляции ОШИМ-1 переходит в ФИМ-l, а ОШИМ-2 соответственно в ФИМ-2. Следовательно, все способы и схемы получения ОШИМ пригодны также и для получения ФИМ.
Перейдем теперь к частотной импульсной модуляции (ЧИМ). При ЧИМ частота периодической последовательности импуль-сов Fп изменяется по закону, отображающему передаваемую ин-формацию. Так же, как и при ФИМ, канальные импульсы сдвига-ются относительно тактовых точек, однако сдвиги импульсов под-чиняются другой закономерности. Можно показать [2], что при ЧИМ моменты возникновения импульсов определяются следую-щим соотношением:
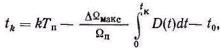 (5.24)
(5.24)
где  — максимальная девиация частоты повто-рения
— максимальная девиация частоты повто-рения 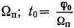 —— постоянный для всех импульсов сдвиг.
—— постоянный для всех импульсов сдвиг.
Один из возможных способов получения ЧИМ основан на использова-нии различия между частотной и фазовой модуляциями [см. выражение (5.26) и (5.27)]. Для получения ЧИМ этим способом используются схемы получения ФИМ, однако, модулирующее напряжение r(t) перед подачей на модулятор про-пускают через линейный четырехполюсник, амплитудно-частотная характеристи-ка которого меняется обратно пропорционально частоте модуляции, что и тре-буется при ЧИМ.
Второй способ получения ЧИМ основан на преобразовании частотно-моду-лированного колебания посредством двустороннего ограничения с последующим дифференцированием в последовательность импульсов модулированных по ча-стоте повторения. Иногда для получения ЧМ применяется мультивибратор, ча-стота колебаний которого может легко модулироваться.
§ 5.2. Обзор методов расчета частотных спектров импульсно-модулированных сигналов
Спектр периодической последовательности импульсов F(t) [см. формулу (3.103)] определяется рядом
Фурье:
(5.29)
где
(5.30)
—коэффициенты ряда, n=0, ±1, ±2 ...
На интервале t2 t1 выражение F(t) заменим функцией f(t—t0), описывающей отдельный импульс последовательности (см. рис. 3.18). Если при этом пределы интегрирования распро-странить до ± и ввести
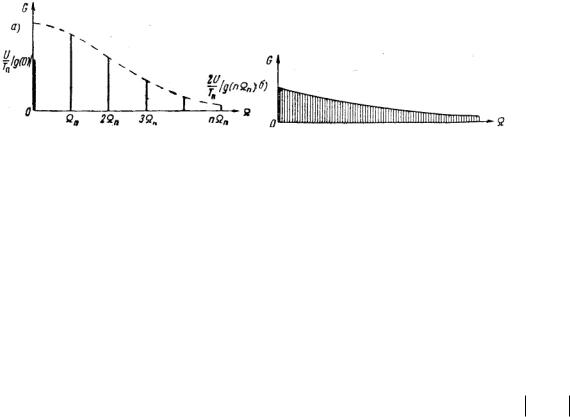
замену переменной интегрирования, приняв x t t0 , то соотношение (5.30) можно представить в следующем виде:
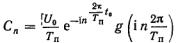 (5.31)
(5.31)
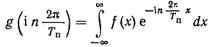 (5.32)
(5.32)
—комплексная спектральная плотность импульса f(x).
После подстановки выражения (5.31) в ряд (5.29) получается выражение для частотного спектра периодической последователь-ности импульсов:
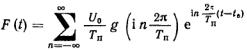 (5.33)
(5.33)
Далее комплексную спектральную плотность представим как
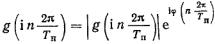 (5.34)
(5.34)
Если при этом воспользоваться формулой Эйлера, то выраже-ние (5.33) можно привести к более употребительной тригонометрической форме:
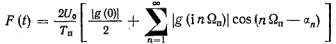 (5.35)
(5.35)
где 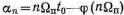 —фаза п-й спектральной компоненты.
—фаза п-й спектральной компоненты.
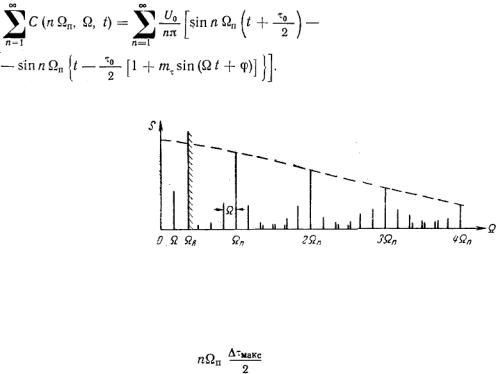
Формула (5.35) достаточно общая и позволяет проследить изменение структуры частотного спектра в зависимости от зна-чений параметров периодической последовательности. В своем составе спектр содержит постоянную составляющую и бесконеч-ную сумму гармоник частоты повторения импульсов (рис. 5.9).
Рис. 5.9
Амплитуды спектральных компонент определяются значениями модуля спектральной плотности
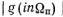 | на гармониках частоты повторения, и, таким образом, форма огибающей частотного спектра периодической последовательности определяется формой f(x) отдельного импульса. При уменьшении периода следования Тп интервал между соседними гармоническими составляющими спектра увеличивается, а их амплитуды возрастают при сохранении постоянного соотношения между ними. С увеличением периода повторения интервал частот между соседними спектральными компонентами сокращается, их число растет, а амплитуда каждой компоненты уменьшается.
| на гармониках частоты повторения, и, таким образом, форма огибающей частотного спектра периодической последовательности определяется формой f(x) отдельного импульса. При уменьшении периода следования Тп интервал между соседними гармоническими составляющими спектра увеличивается, а их амплитуды возрастают при сохранении постоянного соотношения между ними. С увеличением периода повторения интервал частот между соседними спектральными компонентами сокращается, их число растет, а амплитуда каждой компоненты уменьшается.
При неограниченном увеличении Тп периодическая последовательность вырождается в одиночный импульс, а линейчатый спектр становится сплошным (рис. 5.96). Поскольку при всех изменениях Тп соотношение между амплитудами спектральных компонент остается неизменным, форма огибающей спектра также сохраняется. Спектр периодической последовательности радиоимпульсов получается из спектра последовательности видеоимпульсов пере-носом шкалы частот на несущую частоту f0 и дополнением полученного спектра его зеркальным отображением.
Основная энергия сигнала концентрируется в относительно узком частотном диапазоне. При введении соответствующего критерия этот диапазон можно принять за полосу частот, занимаемую спектром последовательности импульсов. Практически эту полосу обычно определяют одним из следующих двух приемов:
1) верхней частотой n п , при которой модуль спектральной плотности импульсов составляет некоторую долю от максимального значения, т. е.
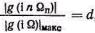 (5.36)
(5.36)
где d= 0,01 0,2 в зависимости от допустимых искажений формы импульсов на приемной стороне;
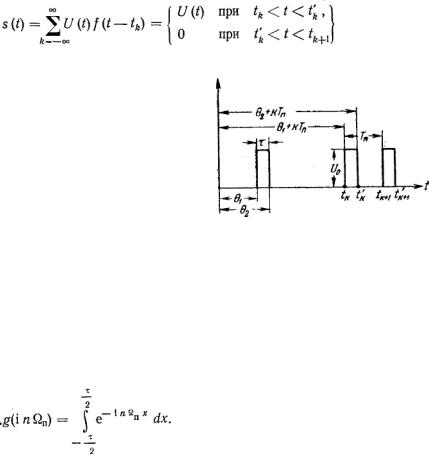
2) верхней частотой n п , ограничивающей область спектра, в которой заключена основная часть всей его энергии. Этот метод определения полосы основан на вычислении функции распределе-ния энергии [8] следующего вида:
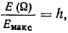 (5.37)
(5.37)
где h 1 - некоторая величина, определяемая допустимыми иска-жениями формы импульсов на выходе приемной части;
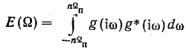 - энергия спектра в полосе
- энергия спектра в полосе 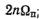
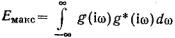 - полная энергия спектра.
- полная энергия спектра.
Расчет полосы частот, занимаемой спектром периодической последовательности импульсов различной формы, первым способом проводится в работе [2], а вторым — в [8].
3. Нестатистические методы расчета частотных спектров модулированных последовательностей импульсов
Из многочисленных нестатических способов расчета частотных спектров рассмотрим лишь два: метод деформации периодической последовательности и операционный.
Операционный метод—наиболее строгий и позволяет вычис-лить частотные спектры при любой импульсной модуляции, в том числе и комбинированной, для импульсов произвольной формы. Применение этого метода, однако, требует знания теории вычетов и часто сопряжено с определенными математическими трудностями.
Метод деформации периодической последовательности импульсов — более простой и пригоден для любого вида импульсной модуляции, но лишь в случае импульсов прямоугольной формы. Метод формирующего фильтра — удобный прием, позволяющий по спектру прямоугольных импульсов вычислять частотный спектр непрямоугольных импульсов. Таким образом, последний можно рассматривать лишь как дополнение к методу деформации, существенно расширяющее его возможности.
Метод деформации периодической последовательности прямоугольных импульсов. Модулирован-ная последовательность импульсов прямоугольной формы опреде-ляется соотношением, вытекающим из рис. 5.10:
|
f t tk 1 |
(5:38) |
|
Здесь |
; U(t) —амплитуда импульсов; |
||
|
Рис. 5.10.
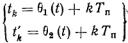 (5.39)
(5.39)
функции, определяющие положе-ние переднего и заднего фронтов импульсов соответственно.
Нетрудно убедиться, что соот-ношение (5.38) при соответствую-щем выборе изменяющихся параметров определяет любой из рас-смотренных выше видов импульс-ной модуляции. Если все параметры в этом соотношении зафиксировать, т. е. принять 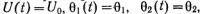 , то получится периодическая последовательность импульсов прямоугольной фор-мы.
, то получится периодическая последовательность импульсов прямоугольной фор-мы.
В случае импульсов прямоугольной формы длительностью т и при f(t—tk) = 1 комплексная спектральная плотность (5.32)

В результате интегрирования
(5.41)
Подставляя это значение спектральной плотности в соотношение (5.35), получаем
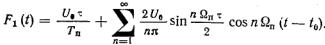 (5.42)
(5.42)
Применительно к рассматриваемому случаю (рис. 5.10)
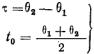 (5.43)
(5.43)
Для любого фиксированного момента t=t1 можно вычислить значения F(t) и F1(t). При этом нетрудно убедиться, что они совпадают, т. е.
Предположим, что параметры, входящие в формулу (5.42), являются функциями времени, т. е. U0=U(t),1= 1(t), 2= 2(t). Тогда, переходя к временному представлению соотношения (5.42), по-лучим новую, уже непериодическую функцию, деформированную относительно исходной, определяемой соотношением (5-40):
(5.44)
Изменение какого-либо параметра последовательности импульсов s(t) в процессе модуляции можно, таким образом, рассматри-вать как деформацию периодической последовательности F(t). Для любого фиксированного момента времени t при соответствую-щем подборе параметров U0, 1 и 2 периодической последова-тельности можно добиться ее совпадения с деформированной последовательностью, т. е.
Следовательно, для того же момента времени соотношение (5.44) возможно представить .в эквивалентной тригонометрической форме:
(5.45)
Формула определяет частотный спектр деформированной последо-вательности импульсов.
Для вычисления частотного спектра модулированной последовательности s(t) методом деформации, прежде всего, необходимо подобрать деформирующие функции Uд=U(t), 1= 1(t) и 2= 2(t) так, чтобы деформированная последовательность sд(t) в любой момент вре-мени совпадала с последовательностью s(t),
частотный спектр которой надлежит найти, т. е.
sд tk s tk
4. Понятие о статистических методах расчета частотных спектров
Рассматриваются два способа вычис-ления спектров нестационарных импульсных случайных процессов: непосредственный и способ, основанный на предварительном вычислении функции корреляции исследуемою случайного процесса.
Рис. 5.11
При непосредственном вычислении энергетического спектра нестационарного импульсного случайного процесса (5] рассматривается одна из усеченных его реализации (например, (-тая), которая может быть задана следующим соотно-шением (рис. 5.11):
(5.67)
где
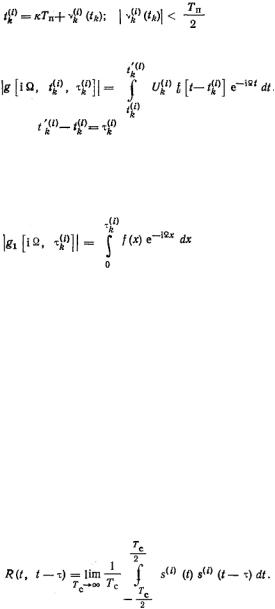
— моменты начала переднего фронта импульсов, 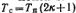 —длительность реализации. Спектральная плотность к-го импульса i-той реализации
—длительность реализации. Спектральная плотность к-го импульса i-той реализации
Здесь — длительность k-го импульса.
Вводя замену переменной интегрирования 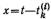 получаем
получаем
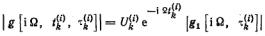 (5.68)
(5.68)
где
(5.69)
|
i |
— спектральная плотность импульса длительностью |
k и единичной амплитуды. |
Спектральную плотность всей (-той реализации случайного процесса мож-но получить как сумму спектральных плотностей отдельных импульсов.
В случае нестационарного случайного процесса энергетический спектр 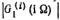 изменяется от реализации к реализации, поэтому для определения спектра случайно модулированной последовательности необходимо дополнительное усреднение значения (5.71) по всем реализациям:
изменяется от реализации к реализации, поэтому для определения спектра случайно модулированной последовательности необходимо дополнительное усреднение значения (5.71) по всем реализациям:
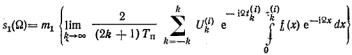 (5.72)
(5.72)
где m1{...} означает операцию усреднения.
Формула (5.72) дает искомый энергетический спектр импульсного случайного нестационарного процесса; она определяет метод вычисления этого спектра.
При втором способе вычисления энергетического спектра импульсного слу-чайного процесса [6], как и в предыдущем случае, исходят из усеченной реализации процесса (5.67), для которой сначала вычисляют функцию автокорреляции по формуле
Энергетический спектр процесса на основании теоремы Винера-Хинчина можно найти как преобразование Фурье от усредненной по времени автокорреляционной функции процесса, т. е.
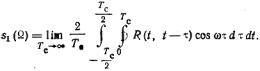 (5.73)
(5.73)
Статистические методы расчета частотных спектров модулированных после-довательностей импульсов позволяют получить достаточно полные сведения о структуре и характере изменения спектров для различных случаев модуляции.
§ 5.3. Частотные спектры и способы демодуляции импульсных сигналов
Высокочастотный сигнал, несущий информацию всех каналов, поступает на вход приемного устройства, усиливается и далее подвергается демодуляции.
Разделение и демодуляция канальных сигналов в этом случае осуществляются оператором или автоматически в процессе рас-шифровки полученных записей. Однако для реализации той же точности, что и при аналоговом методе, здесь требуется значительно более высокая частота повторения импульсов. Вместо
Fп / Fв 2 (см. рис. 3.16), здесь 5 6 .
2.Амплитудная импульсная модуляция
Частотный спектр АИМ-1 и АИМ-2. Чтобы вычислить частотный спектр АИМ-1 для любой формы импульсов, восполь-зуемся формулой (5.7), в которой D (t) определим соотношением (5.49). Тогда
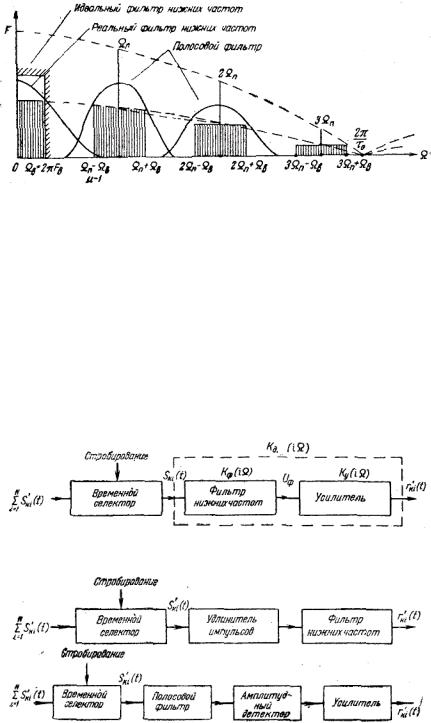
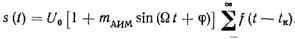 (5.74)
(5.74)
Для импульсов прямоугольной формы частотный спектр АИМ-1 был найден ранее [см. формулу (5.50)]. Примерный вид этого спектра показан на рис. 5.12.
Рис. 5.12
спектр АИМ-1 можно представить в следующей форме:
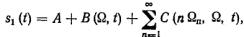 (5.76).
(5.76).
где А — постоянная составляющая;
В( ,t) —компонента спектра, отображающая переданные сообщения [модулирующую функцию D(t)];
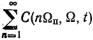 — бесконечная сумма составляющих, кратных тактовой частоте п с семейством боковых, расположенных по обе стороны от n п на расстоянии .
— бесконечная сумма составляющих, кратных тактовой частоте п с семейством боковых, расположенных по обе стороны от n п на расстоянии .
Основные схемы и способы демодуляции АИМ. Из анализа частотного спектра амплитудномодулированной последовательности импульсов (рис. 5.12) вытекают два способа демодуляции АИМ:
1)Непосредственное выделение сообщения из спектра АИМ с помощью фильтра нижних частот. Функциональные схемы демодуляторов, реализующие этот способ, изображены на рис. 5.14 и 5.15.
2)Выделение одной из компонент тактовой частоты n п вместе с боковыми n п± с помощью полосового фильтра (рис. 5.12).
Рис. 5.14
Наиболее широкое распространение на практике получил метод непосредственной демодуляции с помощью фильтра нижних ча-стот.
Рис. 5.16
Параметры модуляции и требования к характеристикам ка-нального модулятора и демодулятора АИМ выбираются в результате анализа модуляционных и демодуляционных искажений. Этот вопрос рассмотрен в следующем параграфе. АИМ нашла широкое применение в различных системах радиотелефонии, радиотелеметрии и радиотелеуправления. Особенно широко АИМ используется в качестве первой ступени модуляции в радиотелеметрии. При этом простыми средствами удается получить большое число каналов, а использование ЧМ во второй ступени обеспечивает высокую по-мехоустойчивость.
3. Широтная импульсная модуляция
Частотный спектр ОШИМ-1. Пользуясь методом деформации периодической последовательности прямоугольных им-пульсов, в предыдущем параграфе нашли выражение (5.56) для частотного спектра ОШИМ- 1, откуда следует, что спектр имеет сложную структуру и содержит в своем составе следующие ком-поненты:
постоянную составляющую
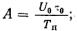 (5.88)
(5.88)
полезную составляющую, отображающую переданное сооб-щение,
 (5.89)
(5.89)
бесконечное число составляющих
(5.90)
Следовательно, помимо постоянной составляющей и полезной компоненты, отображающей сообщения, частотный спектр ОШИМ-1 содержит бесконечное число гармоник частоты повто-
Рис. 5.20
рения (рис. 5.20), каждая из которых, в свою очередь, окружена бесконечным числом компоненте частотами
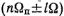 .
.
Амплитуды боковых компонент, группирующиеся вблизи соответствующих гармоник частоты повторения n п , изменяются в соответствии со значениями функций Бесселя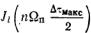 которые, в свою
которые, в свою
очередь, зависят от аргумента |
и номера l, характеризующего порядок этой функции. Это |
группирование более заметно в области небольших значений частоты повторения, т. е. при п , 2 п ,
3 п ... При больших n группирование становится менее заметным. Последнее объясняется тем, что аргумент
функции Бесселя 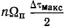 на этих частотах велик, и поэтому спектр боковых полос около этих гармоник расширяется. Поскольку при любом значении п и l функция Бесселя существует, ширина спектра боковых
на этих частотах велик, и поэтому спектр боковых полос около этих гармоник расширяется. Поскольку при любом значении п и l функция Бесселя существует, ширина спектра боковых
около каждой гармоники n п теоретически бесконечна, т. е. спектры полос всех гармоник практически неразделимы. Это обстоятельство вызывает появление искажений при демодуляции, если демодуляция производится с помощью фильтра низких частот.
С ростом девиации макс увеличивается аргумент функции Бесселя, поэтому он всегда сопровождается ростом интенсивности боковых компонент гармоник таковой частоты и, следовательно, увеличением комбинационных искажений.
Основные способы и схемы демодуляции ШИМ. При расчете частотного спектра ШИМ установлено, что он содержит большое число спектральных составляющих около каждой гармоники частоты повторения, и их полосы перекрываются (рис. 5.20). Поэтому единственный, практически приемлемый спо-соб демодуляции ШИМ — использование фильтра нижних частот. Демодуляция ШИМ может быть осуществлена тем же методом, что и демодуляция АИМ (рис. 5.14).
При одинаковой длительности импульсов на входе демодулятора амплитуды полезной составляющей при ОШИМ-1 и АИМ-1 на его выходе примерно одинаковы. Однако, если учесть, что удлинение импульсов возможно при АИМ и невозможно при ШИМ, то демодуляция АИМ может дать больший эффект на выходе.
Широтная импульсная модуляция используется в многоканальных линиях импульсной радиосвязи, а также в некоторых радиотелеметрических системах и системах радиотелеуправления.
4. Фазовая импульсная модуляция
