
- •Лабораторна робота № 1. Форматний ввід/вивід
- •Лабораторна робота № 4. Вказівники та операції над ними
- •Завдання 4.3. Арифметичні дії над вказівниками
- •Лабораторна робота № 5. Одновимірні масиви Рекомендації до виконання лабораторної роботи
- •Лабораторна робота № 6. Двовимірні масиви
- •Лабораторна робота № 7. Символьна інформація та рядки
- •Лабораторна робота № 8. Передача масивів у функцію
- •Лабораторна робота № 9. Перевантаження функцій. Функції зі змінною кількістю параметрів.
- •Лабораторна робота № 10. Структури
- •Список використаної літератури
Лабораторна робота № 6. Двовимірні масиви
Рекомендації до виконання лабораторної роботи
Слід використовувати динамічні масиви зі змінними розмінностями, пам’ять під такі масиви виділяється в циклах.
Введення розмірності масиву та його елементів здійсніть у текстовому файлі з обраним Вами іменем (наприклад: input.txt), а одержані результати виведіть в інший текстовий файл (наприклад: output.txt).
Пояснення. Текстові файли створюються у будь-якому текстовому редакторі до першого запуску програми на виконання. Файли повинні зберігатися в тому самому каталозі, що і Ваша програма. Введення з файлу та виведення у файл здійснюється за допомогою об’єкта fin класу вхідних файлових потоків і об’єкта fout класу вихідних файлових потоків, відповідно. Файлові потоки описані у заголовочному файлі <fstream.h>. Робота з цими об’єктами аналогічна роботі зі стандартними об’єктами cin і cout, тобто можна користуватися тими самими операціями розміщення в потік << і вилучення з потоку >>.
Визначення зазначених об’єктів виконується в тілі головної функції на самому початку у вигляді:
ifstream fin (“input.txt”, ios::in | ios::nocreate);
if (!fin) {
cout<< “Даний файл не знайдено.”<<endl; return 1;}
ofstream fout (“output.txt”);
if (!fout) {
cout << “Неможливо відкрити файл для запису”<<endl;
return 1;}
Якщо текстовий файл збережено в іншому каталозі, тоді слід вказати повний шлях до файлу, дублюючи символ оберненої нахиленої риски, наприклад:
ifstream fin (“c:\\prim\\cpp\\input.txt”, ios::in | ios :: nocreate);
Після визначення об’єктів перевіряється успішність їх створення. Особливо важливо це робити для вхідного файлу, щоб виключити імовірність помилки в імені і розміщенні файлу.
Працюючи з об’єктами класів стандартних потоків, можна паралельно використовувати стандартні об’єкти cin і cout для виведення на екран, а не у файл.
Використовуйте проміжний друк ініціалізованих масивів і величин, що обраховуються.
Задавайте текстові приклади, які б перевіряли всі гілки алгоритму, можливі діапазони значень вихідних даних і ситуації, що можуть скластися при виконанні програми.
Початкові і кінцеві двовимірні масиви виводьте на екран у вигляді матриці, а не стовпчика чи рядка.
Варіанти індивідуальних завдань
Варіант 6.1
Дано цілочисельну прямокутну матрицю. Визначіть:
1). Кількість рядків, що не містять жодного нульового елемента (3 бали);
2). Максимальне з чисел, що зустрічається у заданій матриці більше одного разу (+2 бали).
Варіант 6.2
Дано цілочисельну прямокутну матрицю. Визначіть:
1). Кількість стовпчиків, що не містять жодного нульового елемента (3 бали);
2). Розташувати рядки матриці за зростанням суми додатних парних елементів рядка (+2 бали).
Варіант 6.3
Дано цілочисельну прямокутну матрицю. Визначіть:
1). Кількість стовпчиків, що містять хоча б один нульовий елемента (3 бали);
2). Номер рядка, в якому знаходиться найдовша послідовність однакових елементів (+2 бали).
Варіант 6.4
Дано цілочисельну прямокутну матрицю. Визначіть:
1). Добуток елементів тих рядків, які не містять від’ємні елементи (3 бали)
2). Максимум серед сум елементів діагоналей, паралельних головній діагоналі матриці (+2 бали).
Варіант 6.5
Дано цілочисельну прямокутну матрицю. Визначіть:
1). Суму елементів у тих стовпчиках, які не містять від’ємні елементи (3 бали)
2). Мінімум серед сум модулів елементів діагоналей, паралельних побічній діагоналі матриці (+2 бали).
Варіант 6.6
Дано цілочисельну прямокутну матрицю. Визначіть:
1). Суму елементів у тих рядках, що містять хоча б один нульовий елемент (3 бали);
2). Номери всіх рядків і стовпців всіх седлових точок матриці (+2 бали).
* Примітка: матриця А має седлову точку Аij, якщо Аij є мінімальним елементом в і-му рядку і максимальним у j-му стовпчику.
Варіант 6.7
Сусідами елемента Аij назвемо елементи Akl з і-1≤ k ≤ i+1, j-1 ≤ l ≤ j+1, (k,l)≠(i,j). Елемент матриці називається локальним мінімумом, якщо він строго більший за всіх його сусідів.
1). Знайдіть кількість локальних мінімумів заданої матриці розміром 10х10 (3 бали);
2). Знайдіть суму модулів елементів, розташованих вище головної діагоналі (+2 бали).
Варіант 6.8
Для заданої матриці розміром 8х8. Знайдіть:
1). Такі j i k, коли j-й рядок матриці співпадає з k-м стовпчиком (3 бали);
2). Суму елементів у тих рядках, які містять хоча б один від’ємний елемент (+ 2 бали).
Варіант 6.9
Дано цілочисельну прямокутну матрицю.
1). Розташуйте стовпчики заданої матриці за зростанням сум модулів їх від’ємних непарних елементів (3 бали);
2). Знайдіть суму елементів у тих стовпчиках, які містять хоча б один від’ємний елемент (+2 бали).
Варіант 6.10
Дано цілочисельну прямокутну матрицю.
1). Стисніть задану матрицю, видаляючи з неї рядки і стовпчики, заповнені нулями (3 бали);
2). Знайдіть номер першого з рядків, що містять хоча б один додатній елемент (+2 бали).
Варіант 6.11
Сусідами елемента Аij назвемо елементи Akl з і-1≤ k ≤ i+1, j-1 ≤ l ≤ j+1, (k,l) ≠ (i,j). Операція згладжування дає нову матрицю того ж розміру, кожен елемент якої є середнім арифметичним сусідів відповідного елемента вихідної матриці.
1). Побудуйте результат згладжування заданої дійсної матриці розміром 10х10 (3 бали);
2). У згладженій матриці знайдіть суму модулів елементів, розташованих нижче головної діагоналі (+2 бал).
Варіант 6.12
Дано цілочисельну прямокутну матрицю.
1). Здійсніть циклічний зсув елементів на n елементів вправо або вниз (в залежності від введеного режиму) (3 бали);
2). Передбачте випадок, коли n перевищує кількість елементів у рядку або стовпчику (+2 бали).
Варіант 6.13
Дано цілочисельну прямокутну матрицю.
1). Визначіть номер першого з рядків, який містить хоча б один нульовий елемент (3 бали);
2). Розташуйте рядки заданої матриці за спаданням суми їх від’ємних парних елементів (+2 бали).
Варіант 6.14
Дано квадратну матрицю розміром M x N.
Здійсніть циклічний зсув її елементів таким чином: елементи 1-го рядка зміщуються в останній рядок зверху вниз, з нього – в останній рядок справа наліво, з нього – в перший стовпчик знизу вверх, з нього – в перший рядок; для решти – аналогічно (5 балів).
Варіант 6.15
Дано дійсну квадратну матрицю.
1). Шляхом перестановки її елементів досягніть того, щоб її максимальний елемент знаходився у лівому верхньому куті (0,0), наступний максимальний – на позиції (1,1), наступний за величиною – на позиції (2,2) тощо, тобто в такий спосіб заповнити всю головну діагональ (+3 бали);
2). Знайдіть номер першого з рядків, що не містить жодного додатного елемента (+2 бали).
Варіант 6.16
Дано цілочисельну прямокутну матрицю.
1). Впорядкуйте її рядки за зростанням кількості однакових елементів в кожному рядку (3 бали);
2). Знайдіть номер першого зі стовпців, що не містить жодного від’ємного елемента (+2 бали).
Варіант 6.17
Дано цілочисельну матрицю розміром N x M.
1). Перестановкою її рядків і стовпців досягти того, щоб найбільший елемент опинився у верхньому лівому куті (3 бали);
2). Знайдіть номер першого з рядків, у якому немає однакових елементів (+ 2 бали).
Варіант 6.18
Дано дійсну матрицю розміром NxM.
1). Впорядкуйте її рядки за неспаданням найбільших елементів у рядках матриці (3 бали);
2). Всі відємні елементи замініть на їх модулі (+ 2 бали).
Варіант 6.19
Дано матрицю розміром N x N, яка містить 0 і 1.
1). Розверніть елементи масиву на 900 за годинниковою стрілкою (+ 3 бали);
2). Знайдіть рядок, сума елементів якого є найменшою (+ 2 бали).
Варіант 6.20
Дано дійсну матрицю розміром N х N , всі елементи якої різні.
1) Знайдіть скалярний добуток рядка, у якому знаходиться найбільший елемент матриці, на стовпець з найменшим елементом (+ 3 бали);
2). Змініть місцями відповідні рядок і стовпець (+2 бали).
Варіант 6.21
Дано цілочисельну квадратну матрицю.
1). Визначіть, чи є задана матриця магічним квадратом, тобто такою, в якій сума елементів у всіх рядках і стовпцях однакова (+ 3 бали);
2). Знайти номер стовпця, який містить останній нульовий елемент (+ 2 бали).
Варіант 6.22
Дано матрицю розміром N х N.
1). Зайдіть суму найменших елементів її непарних рядків і найбільших елементів її парних рядків (+ 3 бали);
2). Впорядкуйте елементи у рядках за зростанням (+ 2 бали).
Варіант 6.23
Дано дійсну квадратну матрицю порядку N х N.
1). Знайдіть добуток елементів у рядках, що починаються з відємного елемента (нульові елементи ігнорувати) (+ 3 бали);
2). Для кожного стовпчика просумуйте елементи вище головної діагоналі, значення суми розмістіть замість відповідного елемента головної діагоналі
(+ 2 бали).
Варіант 6.24
Дано дійсну квадратну матрицю порядку N х N.
1). Знайти суму елементів вище, нижче головної діагоналі та на ній (+ 3 бали).
2). Отримати квадратну матрицю того ж порядку, у якій елемент рівний 1, якщо відповідний йому елемент вихідної матриці більший за елемент, розташований на головній діагоналі, інакше - рівний 0.
Варіант 6.25
1 )
Отримайте цілочисельну квадратну
матрицю порядку N, елементами якої є
числа 1, 2, 3, … , розташовані у ній по
спіралі (+ 3 бали):
)
Отримайте цілочисельну квадратну
матрицю порядку N, елементами якої є
числа 1, 2, 3, … , розташовані у ній по
спіралі (+ 3 бали):
2) Поміняти місцями нульовий і N-й стовпчик (+ 2 бали).
Варіант 6.26
Дано дійсну квадратну матрицю.
1) Розбийте матрицю на чотири рівні блоки (рис а.) і знайдіть суму в кожному з них (+ 3 бали);
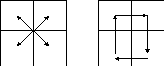
а) б)
2) Змістіть дані у матриці на один блок за годинниковою стрілкою (рис б.)
(+ 2 бали).
Варіант 6.27
Дано дійсну квадратну матрицю порядку n.
1) Знайдіть найменше зі значень елементів, розміщених у заштрихованій частині матриці (+ 3 бали);

2) Змініть місцями елементи у відповідних заштрихованих областях (+ 2 бали).
Варіант 6.28
Дано квадратну цілочисельну матрицю порядку N.
Знайдіть суму значень елементів, що знаходяться у заштрихованій частині даної матриці (+ 3 бали);
Визначіть максимальний і мінімальний елементи у даній частині матриці (+ 2 бали).
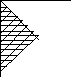
Варіант 6.29
Дано два масиви А(N) і В(M).
Знайдіть рядки масиву А(N), сума елементів яких більша за суму елементів у рядках масиву В(M) (+ 3 бали);
Змініть місцями знайдені у пункті 1 рядки масиву А(N) з відповідними рядками масиву В(M). Передбачте, що маcиви мають різні розмірності. (+ 2 бали)
Варіант 6.30
Дано масив А(N).
1) Отримайте з нього масив В, який складається з елементів масиву А, які знаходяться на парних позиціях (+ 3 бали).
2) В отриманому у пункті 1 масиві змініть порядок розміщення стовпчиків за зростанням кількості у них від’ємних елементів (+ 2 бали).
