
печать кн лабы / KN7
.docxТеоретичні відомості:
Ділення чисел, які представлені у форматі з плаваючою крапкою, відбувається за наступною схемою. Порядок результату визначається шляхом віднімання порядків діленого та дільника. Для визначення мантиси результату виконують ділення мантиси діленого на мантису дільника як правильних дробів у форматі з фіксованою крапкою. Мантиса частки може бути денормалізованою ліворуч. В такому випадку необхідно виконати нормалізацію результату, зсунувши його на один розряд праворуч, та збільшивши порядок на одиницю. Знак мантиси частки визначається шляхом додавання по модулю 2 знаків операндів ділення.
Ділення з відновленням залишку. Нехай ділене X і дільник Y є правильними дробами представлені в прямому коді в n-розрядній сітці. На першому кроці дільник Y вираховується з діленого X і визначається знак нульового залишку R0. R0 означає, що відповідна цифра частки відповідає розряду цілих, тобто 20. Якщо R0 > 0, то в розряді цілих встановлюється 1, формується ознака переповнення і операція ділення припиняється. В протилежному випадку в розряд цілих встановлюється цифра 0, і відбувається відновлення діленого Y шляхом додавання до залишку дільника X. Далі відбувається зсув відновленого діленого на один розряд ліворуч і повторне віднімання дільника. Знак таким чином отриманого залишку R1 визначає першу цифру після коми. Якщо залишок додатній, то цифра частки рівна 1, в протилежному випадку 0. При отриманому додатному залишку його знову зсувають на один розряд ліворуч та виконують віднімання дільника для визначення наступної цифри частки. Якщо ж залишок був від’ємним, то потрібно відновити залишок шляхом додавання до нього дільника. Такі дії повторюють до отримання потрібної кількості цифр.
Ділення без відновлення залишку. Алгоритм виконання операції ділення без відновлення залишку подібний до вищеописаного алгоритму ділення з відновленням залишку. Відмінність полягає в тому, що якщо на певному кроці, в результаті віднімання від поточного залишку дільника, отримується від’ємний залишок, то його наступне відновлення не проводиться, а замість цього на наступному кроці при виконанні порівняння залишку та дільника операція віднімання замінюється операцією додавання.
У випадку коли буде вироблено ознаку переповнення розрядної сітки, необхідно ділене X зсунути праворуч на один розряд і знову розпочати ділення. Після завершення операції частку зсувають ліворуч на те число розрядів, на яке зсувалось праворуч ділене.
Розглянемо приклад.
Нехай X = 1.4375
Y = 3.8125
Необхідно обчислити Z = X*Y.
X2 = 1.0111
Y2 = 11.1101
Число X представлене у форматі SINGLE:
0 01111111 011100000000000000000000
Число Y представлене у форматі SINGLE:
0 10000000 111010000000000000000000
Знаходимо характеристику результату 01111111 – 10000000 + 01111111 = 01111110
Знаходимо знак мантиси 0 0 = 0
Виконуємо ділення мантис за алгоритмом з відновленням залишку:
|
Пояснення |
Операції, операнди, результати |
Цифри частки |
|
1 |
2 |
3 |
|
X -Y R0 |
0|101110000000000000000000 1|000011000000000000000000 1|110001000000000000000000 |
0, |
|
Відновлення Зсув -Y R1 |
0|101110000000000000000000 1|011100000000000000000000 1|000011000000000000000000 0|011111000000000000000000 |
0,1 |
|
Зсув -Y R2 |
0|111110000000000000000000 1|000011000000000000000000 0|000001000000000000000000 |
0,11 |
|
Зсув -Y R3 |
0|000010000000000000000000 1|000011000000000000000000 1|000101000000000000000000 |
0,110 |
|
Відновлення Зсув -Y R4 |
0|000010000000000000000000 0|000100000000000000000000 1|000011000000000000000000 1|000111000000000000000000 |
0,1100 |
|
Відновлення Зсув -Y R5 |
0|000100000000000000000000 0|001000000000000000000000 1|000011000000000000000000 1|001011000000000000000000 |
0,11000 |
|
1 |
2 |
3 |
|
Відновлення Зсув -Y R6 |
0|001000000000000000000000 0|010000000000000000000000 1|000011000000000000000000 1|010011000000000000000000 |
0,110000 |
|
Відновлення Зсув -Y R7 |
0|010000000000000000000000 0|100000000000000000000000 1|000011000000000000000000 1|100011000000000000000000 |
0,1100000 |
|
Відновлення Зсув -Y R8 |
0|100000000000000000000000 1|000000000000000000000000 1|000011000000000000000000 0|000011000000000000000000 |
0,11000001 |
|
Зсув -Y R9 |
0|000110000000000000000000 1|000011000000000000000000 1|001001000000000000000000 |
0,110000010 |
|
Відновлення Зсув -Y R10 |
0|000110000000000000000000 0|001100000000000000000000 1|000011000000000000000000 1|001111000000000000000000 |
0,1100000100 |
|
Відновлення Зсув -Y R11 |
0|001100000000000000000000 0|011000000000000000000000 1|000011000000000000000000 1|011011000000000000000000 |
0,11000001000 |
|
Відновлення Зсув -Y R12 |
0|011000000000000000000000 1|110000000000000000000000 1|000011000000000000000000 1|110011000000000000000000 |
0,110000010000 |
|
Відновлення Зсув -Y R13 |
0|110000000000000000000000 1|100000000000000000000000 1|000011000000000000000000 1|100011000000000000000000 |
0,1100000100001 |
|
Зсув -Y R14 |
1|000110000000000000000000 1|000011000000000000000000 0|001001000000000000000000 |
0,11000001000011 |
|
Зсув -Y R15 |
0|010010000000000000000000 1|000011000000000000000000 1|010101000000000000000000 |
0,110000010000110 |
|
Відновлення Зсув -Y R16 |
0|010010000000000000000000 0|100100000000000000000000 1|000011000000000000000000 1|100111000000000000000000 |
0,1100000100001100 |
|
Відновлення Зсув -Y R17 |
0|100100000000000000000000 1|001000000000000000000000 1|000011000000000000000000 0|001011000000000000000000 |
0,11000001000011001 |
|
Зсув -Y R18 |
0|010110000000000000000000 1|000011000000000000000000 1|011001000000000000000000 |
0,110000010000110010 |
|
1 |
2 |
3 |
|
Відновлення Зсув -Y R19 |
0|010110000000000000000000 0|101100000000000000000000 1|000011000000000000000000 1|101111000000000000000000 |
0,1100000100001100100 |
|
Відновлення Зсув -Y R20 |
0|101100000000000000000000 1|011000000000000000000000 1|000011000000000000000000 0|011011000000000000000000 |
0,11000001000011001001 |
|
Зсув -Y R21 |
0|110110000000000000000000 1|000011000000000000000000 1|111001000000000000000000 |
0,110000010000110010010 |
|
Відновлення Зсув -Y R22 |
0|110110000000000000000000 1|101100000000000000000000 1|000011000000000000000000 0|101111000000000000000000 |
0,1100000100001100100101 |
|
Зсув -Y R23 |
1|011110000000000000000000 1|000011000000000000000000 0|100001000000000000000000 |
0,11000001000011001001011 |
|
Зсув -Y R24 |
1|000010000000000000000000 1|000011000000000000000000 0|000101000000000000000000 |
0,110000010000110010010111 |
Частка Z у форматі SINGLE має вигляд:
0 01111110 10000010000110010010111
Тема роботи: Програмне моделювання машинних алгоритмів ділення чисел з плаваючою крапкою.
Мета роботи: Розглянути машинні алгоритми виконання операції ділення над числами у форматі з плаваючою крапкою. Програмно промоделювати машинні алгоритми ділення чисел з плаваючою крапкою.
Варіант №3
Текст програми на Pascal:
program Project1;
{$APPTYPE CONSOLE}
uses
SysUtils;
const x1=(*250*)'1110010000000000000000000000000000000000000000000000000000000000';
x2=(*050*)'1100001100111000000000000000000000000000000000000000000000000000';
var a,b:string(*DOUBLE*);
procedure SUM(b:string; var c:string;n:integer);
var j,r:integer;
begin
r:=0;
for j:=n downto 1 do
begin
if ord(b[j])+ord(c[j])-96+r>1 then
begin
if ord(b[j])+ord(c[j])-96+r>2 then c[j]:='1'
else c[j]:='0';
r:=1;
end
else
begin
if ord(b[j])+ord(c[j])-96+r=1 then c[j]:='1'
else c[j]:='0';
r:=0;
end;
end;
end;
Function DOD(b:string):string;
var i:integer;
a:string;
Begin
a:=b;
i:=length(a);
while a[i]<>'1' do dec(i);
for i:=i-1 downto 1 do if a[i]='0' then a[i]:='1'
else a[i]:='0';
DOD:=a;
end;
Function Division(a,b:string):String;
var i:integer;
a1,b1,m1,M:string;
begin
m:='';
if a[1]=b[1] then m1:='0'
else m1:='1';
(*A*) a1:=copy(a,2,11);
delete(a,2,11);
insert('01',a,2);
a[1]:='0';
(*B*) b1:=copy(b,2,11);
delete(b,2,11);
insert('01',b,2);
b[1]:='0';
SUM(dod(b1),a1,11);
delete(a1,1,3);
SUM('01111111',a1,8);
Sum(dod(b),a,55);
while a[1]<>'0' do
begin
delete(a,1,1);
a:=concat(a,'0');
Sum('11111111',a1,8);
SUM(b,a,55);
end;
while length(m)<22 do
begin
delete(a,2,1);
a:=concat(a,'0');
if a[1]='0' then Sum(dod(b),a,55)
else Sum(b,a,55);
If a[1]='0' then m:=concat(m,'1')
else m:=concat(m,'0');
end;
Division:=concat(m1,a1,m);
end;
Begin
a:=x1;
b:=x2;
Writeln(a);
Writeln(b);
Writeln(Division(a,b));
readln
End.

Блок-схема процедури Sum
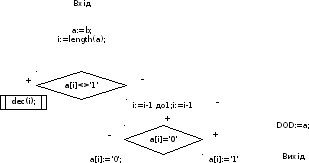
Блок-схема функції Dod

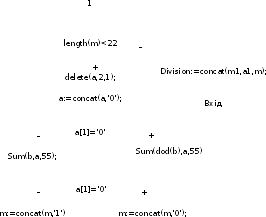
Блок-схема функції Division

Результар роботи програми:

Висновок: Я розглянув машинні алгоритми виконання операції ділення над числами у форматі з плаваючою крапкою. Програмно промоделював машинні алгоритми ділення чисел з плаваючою крапкою
