Лабораторна робота № 5 програмне моделювання машинних алгоритмів додавання та віднімання чисел з плаваючою крапкою

Мета роботи: Розглянути машинні алгоритми виконання операцій додавання та віднімання над числами у форматі з плаваючою крапкою.

Теоретичні відомості:

Будь-яке число Х в позиційній однорідній системі числення з основою р можна записати як X = M*P^K, де М називають мантисою числа Х, а К – порядком цього числа (наприклад, X = 0,4*10⁸, то М = 0,4, Р = 10 , К = 8). Інакше порядок числа називають експонентою. Власне кажучи, число P^K є масштабним коефіцієнтом, на який необхідно помножити число М для того, щоб уникнути переповнення розрядної сітки.

У форматі представлення чисел з плаваючою крапкою, виділяються 3 частини: знак числа (представляється вкрай лівим бітом формату); мантиса числа (представляється у вигляді правильного або неправильного двійкового дробу); порядок числа (представляється в загальному вигляді як ціле число зі знаком). Значення числа А з плаваючою крапкою, представляється у виді :

А_пк=(sign A)^-1*M_a*S^Pa

де sign A - знак 0 - «+», 1 - «-»

S^Pa - порядок числа А, S - підстава порядку.

Число з плаваючою крапкою, називається нормалізованим, якщо старша цифра його мантиси значуща (не 0), у противному випадку число називається не нормалізованим.

Основними особливостями представлення чисел з плаваючою крапкою, у сучасних ЕОМ є :

1. Мантиса числа незалежно від його знака представляється в прямому коді

2. Порядок числа представляється не в явному виді як знакове ціле, а зі зсувом у виді беззнакового цілого числа.

Ця особливість полегшує обробку порядку при виконанні арифметичних операцій. Величина зсуву дорівнює або вазі старшого розряду порядку, або на одиницю менше. Зміщений порядок прийнятий називати характеристикою числа.

3. Як основа порядку використовується значення S=2.

4. У переважній більшості випадків прийняте використання нормалізованих чисел з метою підвищення їхньої точності.

5. При використанні основи порядку, рівній двом, нормалізоване число містить обов'язкову одиницю в старшому розряді мантиси. Це дозволяє не представляти його в явному виді у форматі, що дозволяє збільшити точність числа. Подібне приховання старшого розряду мантиси називається схованим розрядом (схованою одиницею).

6. В ЕОМ для представлення чисел з плаваючою крапкою, прийнято використовувати кілька форматів (як правило, щоб задовольнити суперечливим вимогам підвищення точності чисел і підвищення швидкості їхньої обробки).

Ці формати мають найменування :

а) короткий (одинарної точності) - 32 біта;

б) довгий (подвійної точності) - 64 біта;

в) розширений (розширеної точності) - 80 біт.

Перехід від короткого формату до розширеного супроводжується підвищенням розрядності як мантиси так і порядку.

Короткий формат (В мові програмування PASCAL має назву SINGLE):

31 30 24 23 0

sign

характеристика

Мантиса

Подвійний формат (В мові програмування PASCAL має назву DOUBLE):

63 62 53 52 0

sign

характеристика

Мантиса

Розширений формат (В мові програмування PASCAL має назву EXTENDED):

79 78 64 63 0

Sign

характеристика

Мантиса

У мові програмування Pascal існує ще один тип даних з плаваючою крапкою REAL, який має довжину 6 байт і відрізняється від типу SINGLE тим, що має мантису на 2 байти довшу.

47 46 40 39 0

sign

характеристика

Мантиса

Схована одиниця має місце в короткому і довгому форматах, у розширеному форматі вона представляється в явному виді. Величина зсуву визначається як вага старшого розряду характеристики, зменшена на одиницю.

Додавання чисел з плаваючою крапкою. Нехай задано два числа у нормалізованому вигляді:

де, - мантиси у формі з фіксованою крапкою перед старшим розрядом у нормалізованій формі,

знакові числа з фіксованою крапкою після молодшого розряду.

Треба знайти результат алгебраїчного додавання цих чисел: С=А+В, при цьому, зрозуміло, щоС=ср^mс– число з плаваючою крапкою, оскільки для того, щоб знайти суму двох чисел з різними порядками їх треба попередньо звести до спільного порядку, тобто перетворити один з доданків, наприклад,Втаким чином

(m_заг-m_а)

Після цього можна степінь основи системи числення у загальному степені винести за дужки і виконати лише додавання мантис:

Наприклад.

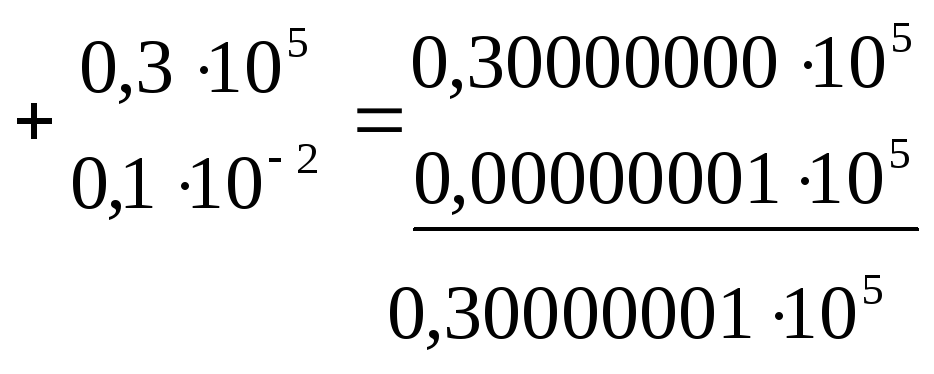
Мантиса числа В після перетворення повинна бути правильним дробом з тим, щоб при додаванні нічим не відрізнятися від звичайних (неперетворених) мантис. Тому перетворенню підлягає завжди менший доданок, оскільки у протилежному випадку відбувається переповнення розрядної сітки мантиси числа, яке перетворюється.

При цьому треба зробити "перенесення" крапки вліво на m_a–m_b – позицій (зсув мантиси вправо). При цьому частина розрядів мантиси може втратитись. Тому арифметичні дії над числами з плаваючою крапкою по своїй суті є наближеними, а не точними. При додаванні чисел в нормальній формі можна виділити 4 етапи.