
ПМ-ДМ-Практ2007-2008
.pdf
ДИСКРЕТНА МАТЕМАТИКА |
2007–2008 |
|
Спецiальнiсть: прикладна математика |
||
|
ПРАКТИЧНЕ ЗАНЯТТЯ № 1
МАТЕМАТИЧНА ЛОГIКА Елементи алгебри висловлювань
Основнi поняття: Висловлювання. Простi i складнi висловлювання, операцiї над висловлюваннями. Таблицi iстинностi висловлювань. Логiчнi формули. Логiчнi закони.
Основнi завдання :
1. Запропонованi висловлювання розбийте на простi висловлювання, позначте простi висловлювання латинськими лiтерами та запишiть у спрощеному виглядi за допомогою основних логiчних операцiй:
1) Якщо дядько Степан їв сьогоднi борщ i сало з часником, то вiн не пiде на зустрiч з англiйською королевою.
2) Кiт Гаврюша тодi i тiльки тодi йде ловити мишей, коли вiн не спить i нiчого не їв не менше трьох днiв.
2. Складiть таблицi iстинностi для формул. Якi з наведених формул є тотожно iстинними, тотожно хибними, виконуваними, спростовними?
1) A _ C ) B , |
AC |
; |
4) A ) BC ) B; |
||||||||
|
|
; |
|
|
_ C)B; |
||||||
2) (A ) B) _ BCA |
5) :(AB |
||||||||||
3) ((A _ B) _ C) ) (A _ B)(A _ C); |
6) A _ B ) ( |
|
|
|
|
||||||
AB _ AB). |
|||||||||||
3. Перевiрте чи є рiвносильними наступнi формули, побудувавши вiдповiднi таблицi iстинностi. Якщо формули рiвносильнi, доведiть те саме, використовуючи рiвносильнi перетворення формул:
1):(A B) _ (A ) B)A = A _ B;
2)(A ) B)(B ) A)(A _ B) = AB;
3)(A ) B)(B ) A)(C ) A) = A C;
4)AC _ AC _ BC _ ABC = A _ BC;
5):((A ) B)(B ) A)) = B ) A;
6)A ) BC = (A ) B)(A ) C).
4. Виразiть основнi логiчнi операцiї (:; ^; _; ©; ); ,) через:
1) : та ^; |
3) |
: та ); |
2) : та _; |
4) |
©, ^ та 1 – так зване представлення у |
|
виглядi полiнома Жегалкiна. |
|
5. Наступнi формули перетворiть рiвносильними перетвореннями так, щоб вони мiстили лише операцiї :; ^; _:
1) (A ) B)(B ) A) ) A _ B; |
3) ((A , |
B |
) ) C) ) (A , |
C |
); |
||
2) (A ) B)(B ) |
|
) ) (C ) A); |
4) (A ) (B , C)) , ((A ) B) , C). |
||||
A |
|||||||
Для отриманих формул побудуйте а) їх заперечення, б) двоїстi, та в) заперечення до двоїстих.
6. Перевiрте правильнiсть мiркувань:
Якщо Джонс не зустрiчав цiєї ночi Смiта, то або Смiт убивця, або Джонс каже неправду. Якщо Смiт – не вбивця, то Джонс не зустрiчав Смiта цiєї ночi, i вбивство сталося опiвночi. Якби вбивство сталося опiвночi, то або Смiт убивця, або Джонс каже неправду. Значить, Смiт – убивця.;
Додатковi завдання :
1.Скiльки iснує нерiвносильних логiчних формул вiд а) двох простих висловлювань; б) вiд трьох простих висловлювань; в) вiд n простих висловлювань?
2.Виразiть основнi логiчнi операцiї (:; ^; _; ©; ); ,) через а) # – стрiлку Пiрса¤; б) j – штрих Шеффера¤; в) виразiть # через j, та навпаки.
¤ A # B = A _ B; A j B = A ^ B.
ДИСКРЕТНА МАТЕМАТИКА |
2007–2008 |
|
Спецiальнiсть: прикладна математика |
||
|
ПРАКТИЧНЕ ЗАНЯТТЯ № 2
МАТЕМАТИЧНА ЛОГIКА Необхiднi i достатнi умови
Основнi поняття: Необхiднi i достатнi умови. Логiчний квадрат. Квантори. Предикати вiд однiєї змiнної. Предикати вiд декiлькох змiнних.
Основнi завдання :
1. Дано висловлювання:
A: ”трикутник рiвнобедренний”; |
D: ”двi висоти трикутника рiвнi”; |
B: ”два кути трикутника рiвнi”; |
E: ”одна висота трикутника рiвна медiанi”; |
C: ”три кути трикутника рiвнi”; |
F : ”один з кутiв трикутника рiвний 60±”. |
Вiдшукайте пари висловлювань, у яких: а) перше є достатньою умовою для другого; б) кожне з висловлень є необхiдною i достатньою умовою для iншого.
2. Сформулюйте теорему у виглядi: ”Якщо A, то B” та сформулюйте обернену, протилежну та протилежну до оберненої теореми:
1) |
”Якщо m i n - непарнi, то непарним є i |
4) |
”Всi ворони чорного кольору”; |
добуток mn”; |
5) |
”Рiвнiсть трикутникiв є достатньою |
|
2) |
”(a = 0) ^ (b = 0) ) (a2 + b2 = 0)”; |
умовою їх рiвновеликостi”; |
|
3) |
”Стукни кобилу по носi – махне хво- |
6) |
”Парнiсть суми є необхiдною умовою |
стом”; |
парностi кожного доданку”. |
||
Якi з одержаних теорем iстиннi, а якi – хибнi?
3.Придумайте власну (не обов’язково iстинну теорему) та сформулюйте для неї обернену, протилежну та протилежну до оберненої теореми.
4.Прочитайте наведенi нижче висловлення та з’ясуйте, якi з них iстиннi, а якi – хибнi, вважаючи, що змiннi пробiгають множину R:
1) 8x9y(x + y = 7); |
4) 9y9x(2x + y = 7); |
x > |
|
x < |
|
|||||
y |
x |
x |
|
y |
= 7); |
x |
1) _ ( |
0))); |
||
2) 9 8 |
( |
|
+ |
|
5) 8x((x > 2 ) , (( |
|
|
|||
3) 8x8y(x + y = 7); |
6) 9b8a9x(x + ax + b = 0). |
|
|
|||||||
5. Для наступних предикатiв за допомогою кванторiв побудуйте всi можливi висловлювання та з’ясуйте, якi з них iстиннi, а якi – хибнi:
2 |
|
> y |
|
|
|
|
1) (x ¡ 3)(x + 3) = x ; |
3) x |
; |
|
|
||
2 |
|
2 |
) ) (x = y). |
|||
2) (x > 0) _ (x = 0) _ (x < 0); |
4) (x |
= y |
||||
6. Нехай P (x) означає ”x – просте число”, E(x) означає ”x – парне число”, O(x) – ”x – непарне число”, D(x; y) – ”y дiлиться на x”. Перекладiть на українську мову такi символiчнi записи:
1) E(2) ^ P (2); |
3) |
8x(O(x) ) 8y(P (y) ) :D(x; y))); |
2) 9x(E(x) ^ D(2; x)); |
4) 9x(E(x) ^ P (x)) ^ :(O(x) ^ P (x))^ |
|
|
|
^9y(x 6= y ^ E(y) ^ P (y)). |
7. Знайдiть значення iстинностi висловлювань та їх заперечень, попередньо записавши у символiчнiй формi:
1) ”iснують такi цiлi числа, якi не дiляться |
3) |
”деякi цiлi числа дiляться на 0”; |
самi на себе”; |
|
|
2) ”iснує цiле число, яке не дiлиться на жо- |
4) |
”iснують многочлени, що мають недiй- |
дне цiле число”; |
снi коренi”. |
|

ДИСКРЕТНА МАТЕМАТИКА |
2007–2008 |
|
Спецiальнiсть: прикладна математика |
||
|
ПРАКТИЧНЕ ЗАНЯТТЯ № 3
МАТЕМАТИЧНА ЛОГIКА Нормальнi форми формул алгебри висловлювань
Основнi поняття: Попередня форма логiчної формули. Елементарнi диз’юнкцiя i кон’юнкцiя. ДНФ. КНФ. Конституенти нуля i одиницi. ДДНФ. ДКНФ.
Основнi завдання :
1.Довести, що кон’юнкцiя двох рiзних конституент одиницi рiвна 0, а диз’юнкцiя двох рiзних конституент нуля рiвна 1.
2.Для заданих логiчних формул:
а) методом рiвносильних перетворень знайдiть попередню форму, ДНФ, ДДНФ, КНФ, ДКНФ;
б) за знайденими ДДНФ побудувати таблицi iстинностi; в) за знайденими таблицями iстинностi побудувати ДКНФ;
г) користуючись картами Карно побудувати мiнiмiзованi ДНФ та КНФ.
1) AC ) B _ ( |
|
) C); |
|
|
)(A _ C); |
||||||||||||||
AB |
4) (A _ BC |
||||||||||||||||||
2) (C ) A) _ (C ) |
|
|
5) ((A ) B) ) (C ) |
|
)) ) ( |
|
) |
|
); |
|
|
||||||||
AB); |
A |
B |
C |
||||||||||||||||
3) A _ ( |
|
) A _ C); |
6) (A ) (B )C)) ) ((A) |
|
) ) (A) |
|
)). |
||||||||||||
B |
C |
B |
|||||||||||||||||
3. Знайдiть логiчну формулу, яка хибна тiльки на визначених чотиризначних наборах значень iстинностi простих висловлень:
1) 0010; 0101; 1111; |
3) |
0000; 0101; 0111; 1111; |
2) 0001; 0010; 0110; |
4) |
1001; 1110. |
4.Скiльки iснує рiзних ДДНФ а) вiд трьох змiнних; б) вiд n змiнних?
5.Знайдiть формули, що задовольняють наступним умовам:
1)формула вiд 3-х змiнних приймає значе- 2) формула вiд 3-х змiнних приймає значе-
ння 1 тодi i тiльки тодi, коли рiвно двi її |
ння, яке мають бiльшiсть її змiнних; |
змiннi приймають значення 1; |
4) формула вiд 3-х змiнних 0 тодi i тiль- |
3) формула вiд 3-х змiнних завжди при- |
ки тодi, коли перша змiнна дорiвнює 1, а |
ймає значення першої змiнної; |
друга i третя – рiвнi. |
Додатковi завдання :
1.Побудуйте булевi многочлени, еквiвалентнi функцiям: iз завдання 2.
2.Знайдiть формулу F (X; Y ) вiд 2-х змiнних таку, щоб формула
(F Y ) X) ) ((X ) Y ) ) F )
була тотожно iстиною.
3. Знайдiть формулу F (X; Y; Z) вiд 3-х змiнних таку, щоб формула
(Z ) XY ) F ) ) F (X ) Y )Z
була тотожно iстиною.
ДИСКРЕТНА МАТЕМАТИКА |
2007–2008 |
|
Спецiальнiсть: прикладна математика |
||
|
ПРАКТИЧНЕ ЗАНЯТТЯ № 4
МАТЕМАТИЧНА ЛОГIКА Аналiз i синтез релейно-контактних схем
Основнi поняття: Релейно-контактнi схеми. Застосування алгебри логiки до вивчення РКС. Мiнiмiзацiя ДДНФ за допомогою карт Карно. Булева алгебра.
Основнi завдання :
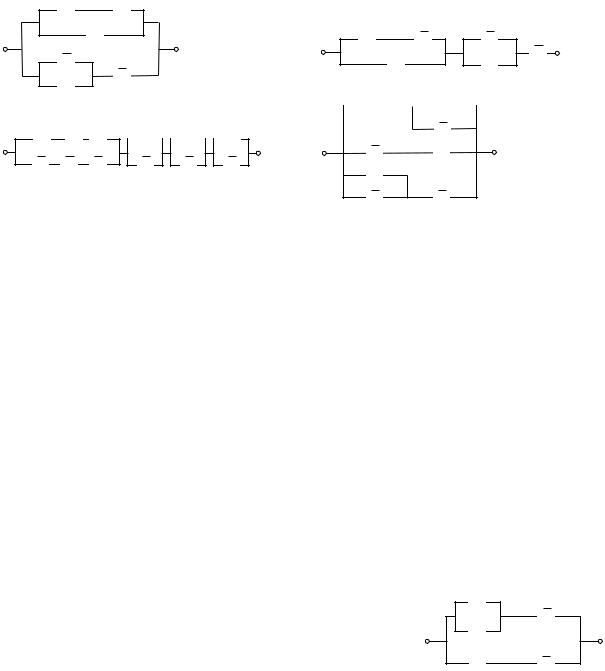
1. Побудуйте РКС, що вiдповiдають заданим логiчним формулам:
1) |
|
( |
|
|
|
|
|
|
|
|
|
|
2) A , |
|
|
|
|
A |
BC _ A _ B); |
AB; |
|||||||||||||||
3) A(BC _ |
|
) _ |
|
( |
|
|
|
|
4) A _ C ) B _ ( |
|
) C). |
||||||
BC |
A |
BC _ BC); |
AB |
||||||||||||||
2. Спростiть РКС, звiвши вiдповiднi їм логiчнi формули до ДДНФ та мiнiзувавши останнi методом карт Карно:
X
1)
Z
X |
Y |
3)
X |
Y |
Z |
X |
Y |
Z |
Y
2) |
|
X |
X |
Y |
|
|
|
Z |
|
Z |
Y |
Z
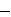 X
X 
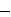 Z
Z 
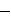 Y
Y
Y |
X |
Z |
 Z
Z 
 X
X 
4) |
Y |
Z |
X |
Z |
|
Y |
Z |
3. Побудуйте найпростiшi РКС, якi не проводять струм лише при таких наборах змiнних:
1) 0011; 1110; 0110; |
2) 0011; 0000; 1100. |
4.Кожен iз трьох членiв комiтету голосує ”за”, натискаючи на кнопку. Побудуйте мiнiмальну схему, через яку проходив би струм тодi i тiльки тодi, коли не менше двох членiв комiтету голосують ”за”.
5.Та ж сама задача для п’яти членiв комiтету, причому схема не проводить струму, якщо голова комiтету голосує ”проти”.
6.На весь пiд’їзд трьохповерхового будинку працює лише одна лампочка. Побудуйте схему так, щоб можна було вмикати i вимикати лампочку на кожному поверсi.
7.Побудуйте РКС з п’ятьма вимикачами, яка проводить струм тодi i тiльки тодi, коли замкнутi всi вимикачi або не замкнутий жоден.
Додатковi завдання :
1. Придумайте цiкаве застосування РКС та побудуйте вiдповiдну мiнiмiзовану РКС.
2. Який контакт потрiбно поставити на порожнє мiсце, щоб функцiя провiдностi отриманої схеми стала рiвно-
сильною X.
X |
X |
Y |
Y |

ДИСКРЕТНА МАТЕМАТИКА |
2007–2008 |
|
Спецiальнiсть: прикладна математика |
||
|
ПРАКТИЧНЕ ЗАНЯТТЯ № 5
ТЕОРIЯ МНОЖИН Множини. Операцiї на множинах
Основнi поняття: Множина. Елементи множини. Операцiї над множинами. Дiаграми Ейлера-Вена. Принцип двоїстостi. Зв’язок з алгеброю логiки. Булеан.
Основнi завдання :
1. Нехай:
U = f1; 2; 3; 4; 5; 6; 7; 8; 9g;
A = f1; 3; 5; 7g; B = f3; 4; 5g; C = f5; 6; 7; 8g. Знайдiть:
1) ((A \ C) [ B) £ (B n (A n C)); |
3) (CU (A [ C)) £ (A \ (CU B n CU A)); |
|||
2) ((B n C) \ A) £ (CU B [ CU (A [ C)); |
4) (CU (A [ B [ C)) £ ((A n B) n C). |
|||
2. Задайте множини у висловлюванiй формi: |
||||
1) |
3; 4; 5; : : :; |
4) |
множина, складається з чисел виду 2n, |
|
2) |
множина натуральних непарних чисел; |
де n 2 N0; |
||
3) |
f |
0; 10; 17 ; |
5) |
; – порожня множина; |
|
g |
6) |
множина правильних дробiв. |
|
3. Доведiть, що
1)A n (B n C) = (A n B) [ (A \ C);
2)A \ (B [ C) = (A \ B) [ (A \ C);
3)(A \ B) n C = (A n C) \ (B n C);
4)CU (A \ B) = CU A [ CU B;
5)CU (A [ B) = CU A \ CU B;
6)A n (B [ C) = (A n B) \ (A n C).
4. Множина A складається з цiлих чисел, що дiляться на 4, множина B – iз цiлих чисел, що дiляться на 10, а множина C – iз цiлих чисел, що дiляться на 75. З яких чисел складається множина A \ B \ C?
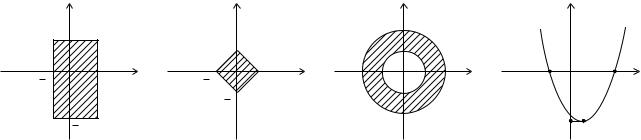
5. Множина A складається з точок M(x; y) площини, для яких jxj · 3, а
jyj < 2, B – множина точок площини, для яких x2 + y2 · 9, а множина C iз точок площини, для яких x > 0. Зобразiть множину
1) (A \ B) n C; |
2) A [ B n C. |
6. Зобразiть за допомогою кругiв Ейлера: |
|
1) множини опуклих чотирикутникiв, |
3) множину дiйсних, рацiональних, цiлих, |
трапецiй, паралелограмiв, прямокутникiв, |
додатнiх, iррацiональних, непарних, про- |
ромбiв, квадратiв; |
стих, комплексних чисел; |
2) множини жiнок, дочок, матерiв, бабусь, |
4) множини людей, будiвельникiв, жiнок, |
викладачiв; |
чоловiкiв, дiтей (< 18 рокiв). |
7.Користуючись кругами Ейлера, розв’яжiть таку задачу: В кривавiй битвi
85iз 100 пiратiв втратили одне око, 80 - одне вухо, 75 - одну руку i 70 - одну ногу. Яке найменше число тих, хто втратив одночасно око, вухо, руку i ногу?
8.Перевiрте справедливiсть iмплiкацiй для довiльних множин A; B; C:
1) (A n B = C) ) (A = B [ C); |
2) (A = B [ C) ) (A n B = C). |
9.Довести, що перетин множин дiсних коренiв многочленiв f(x) i g(x) з дiйсними коефiцiентами спiвпадає з множиною всiх дiйсних коренiв многочлена
'(x) = f2(x) + g2(x).
10.Чи iснують такi множини A; B; C, що A\B 6= ;, A\C = ;, (A\B)nC = ;?
Додатковi завдання :
1.Доведiть теорему: якщо jAj = n, то jP (A)j = 2n.
2.Спростiть вираз:
1)A [ B [ C [ D\A\B\C\D[A [ B [ C; 2) (A [ B [ C) \ (A [ B) n (A [ (B n C)) \ A.
ДИСКРЕТНА МАТЕМАТИКА |
2007–2008 |
|
Спецiальнiсть: прикладна математика |
||
|
ПРАКТИЧНЕ ЗАНЯТТЯ № 6
ТЕОРIЯ МНОЖИН Вiдношення
Основнi поняття: Декартовий добуток множин. n-арне вiдношення. Способи задання вiдношень. Бiнарнi вiдношення. Властивостi бiнарних вiдношень.
Основнi завдання :
Нижче в задачах №№ 1-4 будуть використанi такi вiдношення:
|
|
|
|
|
|
. |
® = f(¡1; 2); (0; 3); (1; 4); (1; 5)g; |
2 . |
|||||
± = f(x; y) 2 N2 j y.xg; |
||||||
¯ |
= f(¡5 |
; |
¡1) |
; (0; 0); (6; 1); (1; 5) |
g; 3 |
" = f(x; y) 2 Q j 2x · 3yg; |
|
|
2 |
||||
° = f(x; y) 2 R j x 2 [¡1; 1]; y = x g; |
¸=”не бути взаємно простим” на множинi |
|||||
M6. |
||||||
1.Задайте вiдношення ¸ за допомогою: характеристичної властивостi, перелiком пар, графом, графiком, стрiлками, матрицями.
2.Для вiдношень ®; ¯; °; ±; "; ¸ знайти область визначення, множину значень та побудувати оберненi вiдношення.
3.Навести приклади унарного, бiнарного, тернарного вiдношень, заданих на множинi квадратних матриць n-го порядку.
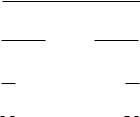
4.За графiчним поданням бiнарних вiдношень записати їх у висловлюванiй формi:
1) |
y |
|
2) |
|
y |
3) |
y |
4) |
y |
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
1 |
0 |
2 |
x |
1 |
0 1 |
x |
0 1 2 x |
1 |
0 |
2 x |
|
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
5. Побудуйте композицiю ® ± ¯ i ¯ ± ® та порiвняйте їх:
1)® = f(¡1; 2); (0; 3); (1; 4); (1; 5)g,
¯= f(¡5; ¡1); (0; 0); (6; 1); (1; 5)g;
2)® =”бути батьком”,
¯=”бути ровесником”
на множинi всiх людей;
3)® = f(4; 1); (4; 3); (¤; 4); (©; 2)g,
¯= f(3; x); (1; y); (5; z); (4; z)g;
4)® = f(x; y) 2 N2 j x...yg,
¯= f(x; y) 2 N2 j x > yg.
6. Побудуйте оберненi вiдношення для вiдношень ® i ¯ iз попереднього завдання. Наведiть приклад бiнарного вiдношення °, такого, що °¡1 = °.
Додатковi завдання :
1. Доведiть властивостi оберненого вiдношення:
1) (®¡1)¡1 = ®; |
2) (® ± ¯)¡1 = ¯¡1 ± ®¡1. |
ДИСКРЕТНА МАТЕМАТИКА |
2007–2008 |
|
Спецiальнiсть: прикладна математика |
||
|
ПРАКТИЧНЕ ЗАНЯТТЯ № 7
ТЕОРIЯ МНОЖИН
Функцiональнi вiдношення. Вiдношення еквiвалентностi i порядку
Основнi поняття: Властивостi бiнарних вiдношень. Вiдношення еквiвалентностi. Класи еквiвалентностi. Фактор-множина. Вiдношення порядку (строгого, нестрогого,
лiнiйного). Упорядкованi множини. Функцiональнi вiдношення. Iн’єкцiя, сюр’єкцiя, бiєкцiя.
Основнi завдання :
1. Якi iз приведених нижче вiдношень є функцiональними:
|
|
. |
1) ® = f(¡1; 2); (02; 3); (1; 4); (1; 5)g; 3 |
|
2 . |
g; |
3) ® = f(x; y) 2 N2 j y.xg; |
|
2) ® = f(x; y) 2 R j x 2 [¡1; 1]; y = x |
4) ® = f(x; y) 2 Q j 2x · 3yg. |
2.Дайте означення рефлексивного, антирефлексивного, симетричного, антисиметричного, транзитивного бiнарних вiдношень i наведiть їх подання у виглядi графiв.
3.Заповнiть таблицю знаками ”+” або ”–”:
Вiдношення |
Р |
АР |
С |
АС |
Т |
Е |
Д |
П |
”x проживає в одному будинку з y” на множинi |
|
|
|
|
|
|
|
|
всiх жителiв м. Черкаси |
|
|
|
|
|
|
|
|
”x батько або мати y” на множинi всiх людей |
|
|
|
|
|
|
|
|
”x сестра y” на множинi всiх людей |
|
|
|
|
|
|
|
|
”x командир y” на множинi всiх вiйськових |
|
|
|
|
|
|
|
|
”x > y” на R |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
”x.y” на Z |
|
|
|
|
|
|
|
|
”x i y – числа однакової парностi” на Z |
|
|
|
|
|
|
|
|
”x k y” на множинi прямих площини |
|
|
|
|
|
|
|
|
”x ? y” на множинi прямих площини |
|
|
|
|
|
|
|
|
Р – рефлексивне вiдношення; АР – антирефлексивне вiдношення; С – симетричне вiдношення; АС – антисиметричне вiдношення; Т – транзитивне вiдношення; Е – вiдношення еквiвалентностi (Р+С+Т); Д – досконале вiдношення; П – вiдношення (часткового) порядку (АС+Т).
4. Доведiть, що наведенi бiнарнi вiдношення є вiдношеннями еквiвалентностi та побудуйте вiдповiднi фактор-множини:
|
|
2 |
|
. |
|
|
1) |
® = f(a; b) 2 Z |
|
. |
4) |
вiдношення ”мати однакову масть” на |
|
|
j (a ¡ b).7g; |
|||||
2) |
вiдношення паралельностi на множинi |
множинi всiх коней; |
||||
прямих на площинi; |
трикутникiв на |
5) |
вiдношення рiвносильностi на множинi |
|||
3) |
вiдношення подiбностi |
всiх висловлень вiд трьох змiнних; |
||||
площинi; |
|
|
|
6) |
вiдношення ”бути однолiтками” на мно- |
|
|
|
|
|
|
жинi всiх людей. |
|
5. Нехай A = f1; 2; 3; 4; 5; 6; 7g i ® = f(x; y) 2 A2 j (x ¡y).2 ^x > yg Показати, що ® є вiдношенням порядку на A.
Додатковi завдання :
1.Нехай вiдношення < i · визначаються на множинi N звичайним способом. Доведiть, що < ± <6=<, · ± <=<, · ± ¸= N2.
2.Скiльки iснує неiзоморфних вiдношень (часткового) порядку на множенi iз 3-х елементiв? iз 4-х елементiв?
ДИСКРЕТНА МАТЕМАТИКА |
2007–2008 |
|
Спецiальнiсть: прикладна математика |
||
|
ПРАКТИЧНЕ ЗАНЯТТЯ № 8
ТЕОРIЯ МНОЖИН Потужнiсть множини
Основнi поняття: Рiвнопотужнi множини. Потужнiсть множин. Потужнiсть множини N. Зчисленнi множини. Континуум. Множини потужностi континуум.
Основнi завдання :
1. Довести зчисленнiсть наступних множин:
1) |
множини 2N + 1 непарних натуральних |
5) |
множини Q+ додатнiх рацiональних чи- |
чисел; |
сел; |
||
2) |
множини mN натуральних чисел кра- |
6) |
множини Q всiх рацiональних чисел; |
тних фiксованому числу m; |
7) |
множини рацiональних чисел, знамен- |
|
3) |
множини Z цiлих чисел; |
ники яких є степенями числа 2; |
|
4) |
множини цiлих степенiв числа 2; |
8) |
множини Q2 всiх точок площини з ра- |
|
|
цiональними координатами. |
|
2. Вiдобразiть бiєктивно множину точок з iнтервалу (0; 1) на: |
|||
1) |
множину точок прямої; |
3) |
на множину точок квадрату зi стороною |
2) |
множину точок з сегменту [0; 1]; |
рiвною 1; |
|
|
|
4) |
на множину точок n-вимiрного кубу. |
3. Якi потужностi мають множини: |
|
|
|
1) iррацiональних чисел; |
5) |
всiх многочленiв з дiйсними коефiцiєн- |
|
2) |
чисел з iнтервалу (0; 1), в десятковому |
тами; |
|
записi яких є лише цифри 0 i 1; |
6) |
всiх функцiй неперервних на сегментi |
|
3) |
комплексних чисел; |
[a; b]; |
|
4) |
квадратних матриць n-го порядку з дiй- |
7) |
всiх пiдмножин множини чисел з iнтер- |
сними коефiцiєнтами; |
валу (0; 1); |
||
|
|
8) |
всiх трикутникiв площини. |
4.Обчислiть: n + @0, @1 + @2, n ¢ @0, @1 ¢ @2, 2@0, 2@1.
5.Вкажiть множину, яка має потужнiсть бiльшу за 0 i меншу вiд 1. Яка множина має найбiльшу потужнiсть?
Додатковi завдання :
1. Знайдiть в лiтературi опис кривої Пеано та доведiть, що вона проходить через всi точки квадрату. Спробуйте побудувати свою криву, яка проходить через всi точки квадрату.
2. Розглянемо сегмент [0; 1]. Подiлимо його на 3 рiв-
нi частини точками 31 i 32 та заберемо середнiй iн- |
||
тервал |
31; |
32 . Аналогiчну операцiю проведемо над |
двома |
сегментами, що залишилися, i т.д. до не- |
|
¡ |
¢ |
|
скiнченностi. Множина |
точок, |
яка |
залишиться |
вiд |
сегмента в результатi |
таких |
перетворень, назива- |
||
ється множиною Кантора. Вона |
має довжину |
0 |
||
i потужнiсть континуум. Доведiть це. Спробуйте побудувати iншi незчисленнi множини довжини 0.
0
0
|
|
1 |
|
2 |
|
|
||
|
|
3 |
|
3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
1
ДИСКРЕТНА МАТЕМАТИКА |
2007–2008 |
|
Спецiальнiсть: прикладна математика |
||
|
ПРАКТИЧНЕ ЗАНЯТТЯ № 10
АЛГЕБРАЇЧНI СИСТЕМИ Алгебри з однiєю алгебраїчною операцiєю
Основнi поняття: Алгебраїчнi операцiї. Властивостi алгебраїчних операцiй. Алгебри з однiєю алгебраїчною операцiєю (пiвгрупа, група).
Основнi завдання :
1.Чи є алгебраїчними операцiями:
1)операцiя кон’юнкцiя на множинi всiх ло- 3) операцiя композицiї на множинi всiх
гiчних формул; |
вiдношень деякої множини; |
2) операцiя вiднiмання на множинi N; |
4) операцiя додавання на множенi M4 = |
|
f1; 2; 3; 4g. |
2. Наведiть приклади алгебр, в яких операцiї задовольняли б наступним умовам:
1) одна бiнарна операцiя комутативна, але |
4) |
одна бiнарна операцiя iндемпотентна, |
не асоцiативна; |
але не асоцiативна; |
|
2) одна бiнарна операцiя некомутативна i |
5) |
двi бiнарнi операцiї, для яких виконує- |
неасоцiативна; |
ться правий дистрибутивний закон i не ви- |
|
3) двi бiнарнi операцiї, для яких виконує- |
конується лiвий; |
|
ться лiвий дистрибутивний закон i не ви- |
6) |
двi бiнарнi та одна унарна операцiї, при- |
конується правий; |
чому для них не виконується закон де |
|
|
Моргана. |
|
3. Складiть таблицi Келi та перевiрте, чи є утворенi алгебри пiвгрупами або групами:
1) таблицi додавання та множення остач 2) таблиця НСД (найб. сп. дiльник) 2-х чи-
вiд дiлення на 6; |
сел на множинi X = f0; 1; 2; 3; 4; 5; 6g. |
|
4. З’ясуйте, чи є групою (пiвгрупою) кожна iз наступних множин, iз заданими на них операцiями:
1)hZ; +i – цiлi числа вiдносно додавання;
2)h5Z; +i – цiлi числа, кратнi 5, вiдносно додавання;
3)hZ+ [f0g; +i – невiд’ємнi цiлi числа вiдносно додавання;
4)hO; +i – непарнi цiлi числа вiдносно додаванння;
5)hZ; ¡i – цiлi числа вiдносно вiднiмання;
6)hQnf0g; ¢i – рацiональнi числа без 0 вiдносно множення;
7)hQ+; ¢i – додатнi рацiональнi числа вiдносно множення;
8)двiйково-рацiональнi числа, тобто рацiональнi числа, знаменники яких – степенi числа 2, з цiлими невiд’ємними показниками, вiдносно додавання;
9)квадратнi матрицi n-го порядку з дiйсними елементами вiдносно додавання;
10)множина логiчних формул вiдносно операцiї кон’юнкцiя, iмплiкацiя;
11)булеан скiнченної множини вiдносно операцiї об’єднання;
12)hR+; ¤i – додатнi дiйснi числа, якщо операцiя визначається так: a ¤ b = a;
13)hR+; ¤i – додатнi дiйснi числа, якщо
операцiя визначається так: a ¤ b = a2b2;
14)множина пар дiйсних чисел без пари (0; 0) вiдносно операцiї -, заданої так:
(a; b) - (c; d) = (ac ¡ bd; ad + bc);
15)множина пар дiйсних чисел без пари (0; 0) вiдносно операцiї -, заданої так:
(a; b) - (c; d) = (ac + bd; ad).
Додатковi завдання :
1. |
Чи асоцiативна операцiя ¤ на множинi R+, якщо a ¤ b = xyx=jxj? |
2. |
Доведiть, що h[0; 1);-i – група, якщо a-b = fa+bg – дробова частина a+b. |
3. |
Спробуйте узагальнити властивостi асоцiативностi, комутативностi, |
дистрибутивностi на випадок тернарних алгебраїчних операцiй.
ДИСКРЕТНА МАТЕМАТИКА |
2007–2008 |
|
Спецiальнiсть: прикладна математика |
||
|
ПРАКТИЧНЕ ЗАНЯТТЯ № 11
АЛГЕБРАЇЧНI СИСТЕМИ Алгебри з двома алгебраїчними операцiями
Основнi поняття: Алгебри з двома алгебраїчними операцiями (кiльце, тiло, поле). Пiдалгебри. Векторнi простори. Лiнiйнi алгебри.
Основнi завдання :
1. З’ясуйте, якi iз нижче наведених множин є кiльцями (але не полями), а якi полями вiдносно вказаних операцiй (якщо операцiї не вказанi, то вважаємо, що заданi операцiї додавання i множення чисел):
1)hZ; +; ¢i – цiлi числа;
2)hnZ; +; ¢i – цiлi числа, кратнi n;
3)множина всiх цiлих степенiв числа 2;
4)множина всiх висловлювань вiдносно операцiй диз’юнкцiї та кон’юнкцiї;
5)булеан деякої множини вiдносно операцiй об’єднання i перерiзу;
6)множина остач вiд дiлення на 6 вiдносно операцiй додавання i множення остач;
7)множина остач вiд дiлення на 5 вiдносно операцiй додавання i множення остач;
8)множина невироджених квадратних матриць n-го порядку вiдносно операцiй додавання i множення матриць;
9)множина всiх пар (a; b) рацiональних чисел, де a =6 0, а операцiї додавання i множення визначаються рiвностями:
(a; b) + (c; d) = (a + c; b + d);
(a; b) ¢ (c; d) = (ac; bc + d);
10) множина R£R вiдносно операцiй додавання i множення визначених рiвностями:
(a; b) + (c; d) = (a + c; b + d); (a; b) ¢ (c; d) = (ac + bd; ad + bc);
11) множина R£R вiдносно операцiй додавання i множення визначених рiвностями:
(a; b) + (c; d) = (a + c; b + d); (a; b) ¢ (c; d) = (ac; ad + bc);
12)функцiї з дiйсними значеннями, непе-
рервнi на вiдрiзку [¡1; 1], вiдносно додавання i множення функцiй;
13)всi матрицi виду
³a ´ a; b 2 Q;b
2b a
вiдносно додавання i множення матриць;
14) всi матрицi виду |
; a; b 2 R |
|||
³ |
¡b |
a |
´ |
|
|
a |
b |
|
|
вiдносно додавання i множення матриць; |
|||||||
15) |
|
|
p |
||||
числа виду a + b 3 2, a; b 2 Z; |
|||||||
|
|
|
p |
|
|
||
16) |
числа виду a + bp |
|
3 |
, a; b 2 Q; |
|||
17) |
числа виду a + b |
5 |
, a; b 2 Q; |
||||
18) |
комплекснi числа виду a + bi, a; b 2 Z; |
||||||
19) |
множина чисел виду |
||||||
|
x + yp3 |
|
+ zp3 |
|
; x; y; z 2 Q: |
||
|
2 |
22 |
|||||
2. На множинi многочленiв вiд змiнної t зi звичайним додаванням розглядається операцiя множення, що визначається правилом: (f ± g)(t) = f(g(t)). Чи є дана множина кiльцем?
Додатковi завдання :
1. Для яких чисел n = 2; 3; 4; 5; 6; 7 iснує поле iз n елементiв?
