Стереометрія

Бічна поверхня правильної трикутної піраміди в три рази більша площі основи. Площа круга, вписаного в основу, чисельно дорівнює радіусу цього круга. Знайти об’єм піраміди.
В правильній зрізаній трикутній піраміді сторона більшої основи , а меншої – . Бічне ребро утворює з основою кут . Знайдіть площу перерізу, який проходить через бічне ребро і вісь піраміди.
Основою піраміди SАВС є трикутник АВС, у якому АВ і АС утворюють між собою кут  і АВ = АС = а. Грань SВС перпендикулярна до площини основи, а грані SВА та SСА утворюють з площиною основи кути φ. Знайти бічну поверхню цієї піраміди.
В основі піраміди лежить прямокутний трикутник з периметром Р і гострим кутом . Бічні ребра піраміди нахилені до площини основи під кутом. Знайти об'єм піраміди.
Обчислити об'єм правильної трикутної піраміди, якщо плоский кут при вершині дорівнює , а радіус кола, описаного навколо бічної грані дорівнюєR.
Дана піраміда, основою якої є прямокутний трикутник з гострим кутом . Бічні ребра піраміди дорівнюютьі нахилені до площини основи під кутом. Визначити об'єм піраміди.
Дана піраміда, основою якої є прямокутний трикутник з гострим кутом . Бічні ребра піраміди дорівнюютьі нахилені до площини основи під кутом. Визначити об'єм піраміди.
Основою чотирикутної піраміди є ромб, довжина меншої діагоналі якого рівна, а величина гострого кута рівна. Кожна бічна грань нахилена до площини основи під кутом. Обчислити бічну поверхню піраміди.
Діагональ бічної грані правильної трикутної призми рівна , і складає кутз площиною другої бічної грані. Знайти об'єм піраміди.
Визначити повну поверхню правильної трикутної піраміди, у якої плоский кут при основі бічної грані , а радіус круга, вписаного в основу, рівний.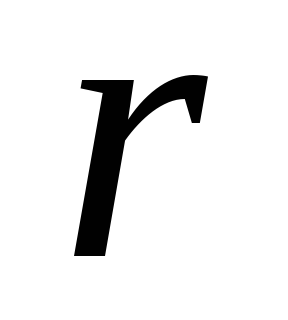
У зрізаному конусі діагоналі осьового перерізу взаємно перпендикулярні. Висота конуса дорівнює 6 см, а кут між твірною й площиною основи 60º. Знайдіть об'єм цього конуса.
Діагональ прямокутного паралелепіпеда дорівнює і утворює з площиною однієї бічної грані кут, а іншої – кут . Знайдіть площу бічної поверхні паралелепіпеда.
Апофема правильної чотирикутної піраміди дорівнює . Бічне ребро піраміди утворює з площиною основи кут. Знайдіть об’єм піраміди.
Через сторону правильного трикутника проведено площину. Яка утворює з площиною трикутника кут 30. Знайдіть кути, які утворюють дві інші сторони трикутника з цією площиною.
Основа піраміди – рівнобедрений трикутник з бічною стороною і кутомпри основі. Бічна грань піраміди, що містить основу цього трикутника, перпендикулярна до площини основи, а дві інші нахилені до неї під кутом. Знайдіть об’єм піраміди.
Через сторону нижньої основи і середину протилежного бічного ребра правильної трикутної призми проведено переріз під кутом 45 до площини основи. знайдіть об’єм призми. Якщо площа перерізу дорівнює см.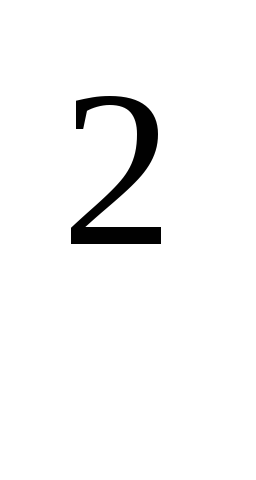
Через дві твірні конуса, кут між якими дорівнює , проведено переріз, який утворює з площиною основи конуса кут. Знайдіть площу бічної поверхні конуса.
Основа прямої призми – ромб з гострим кутом . Діагональний переріз призми, що проходить через більшу діагональ основи, має площуS. Знайдіть площу бічної поверхні призми.
Через дві твірні конуса проведено площину, яка нахилена до площини його основи під кутом . Ця площина перетинає основу конуса по хорді, яку видно із центра його основи під кутом. Знайдіть площу бічної поверхні конуса, якщо його твірна дорівнює.
В правильній трикутній піраміді сума кутів, які утворені апофемою піраміди з площиною основи і бічним ребром з тією ж площиною, дорівнює . Знайдіть ці кути.