Розділ 5. Геометричні задачі Планіметрія

1. У коло радіуса R вписано трикутник з кутами 15⁰ і 60⁰. Знайдіть площу цього трикутника.

2. Коло, центр якого на гіпотенузі, торкається більшого катета трикутника і проходить через вершину протилежного гострого кута. Знайти його радіус, якщо катети 3 см і 4 см.

3. В прямокутний трикутник вписано півколо так, що діаметр кола лежить на гіпотенузі, а центр кола ділить гіпотенузу на відрізки 15 см і 20 см. Знайдіть площу трикутника.

4. Прямі, що містять бічні сторони рівнобічної трапеції перетинаються під прямим кутом. Знайти довжини сторін трапеції, якщо площа її 12 см, а висота 2 см.

5. Знайти площу круга, вписаного в рівнобічну трапецію, якщо її більша основа дорівнює , а кут при меншій основі дорівнює 120.

6. Площа рівнобічної трапеції, описаної навколо круга, дорівнює 8 см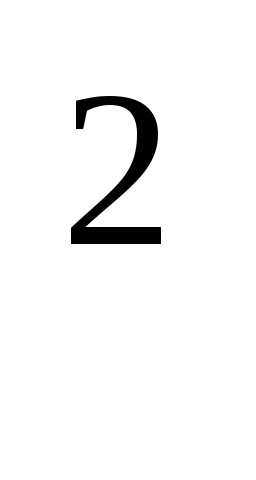. Визначити сторони трапеції, якщо кут при основі дорівнює 30.

7. Площа рівнобічної трапеції, описаної навколо круга дорівнює S. Визначити бічну сторону, якщо гострий кут при основі дорівнює .

8. Довжини паралельних сторін трапеції 25 см та 4 см. А довжини непаралельних сторін 20см та 13см. Знайти висоту трапеції.

9. На гіпотенузі АВпрямокутного трикутникаАВСвибрана точкаК, для якоїСК = ВС. ВідрізокСКперетинає бісектрисуАМв її середині. Знайти кути трикутникаАВС.

10. В рівнобедрений трикутник з основною 6 см і бічною стороною 5 см вписано коло. До кола проведено дотичну перпендикулярно основі. Знайти площу трикутника, який відсікає від даного трикутника ця дотична.

11. В трикутнику довжини двох сторін 6 і 3 см. Знайти довжину третьої сторони, якщо півсума висот, проведених до даної сторони дорівнює третій висоті.

12. Квадрат зі стороною a зрізаний по кутам так, що утворився правильний восьмикутник. Визначити площу цього восьмикутника.

13. Коло радіуса R вписане в рівнобічну трапецію. Верхня основа трапеції в два рази менша її висоти. Знайти площу трапеції.

14. Знайти висоту прямокутної трапеції, якщо її менша діагональ дорівнює більшій основі. Площа трапеції дорівнює S, гострий кут дорівнює α.

15. В квадрат ABCD вписаний інший квадрат KLMN, так що його вершини лежать на сторонах першого квадрата, а сторони складають зі сторонами першого квадрата кути по 30˚. Яку частину площі даного квадрата складає площа вписаного?

16. В прямокутнику ABCD сторона АВ в три рази більша сторони ВС. Всередині прямокутника лежить точка N, причому AN=,BN=,DN=.Знайти косинус кута BAN і площу прямокутника ABCD.

17. Визначити кут в ромбі, якщо його площа дорівнюєQ, а площа вписаного круга дорівнює S.

18. Основитатрапеціїдорівнюютьта. Знайдіть довжину відрізка, який відрізається діагоналями трапеції на її середній лінії.

19. Довести, що в будь-якому трикутнику сума медіан 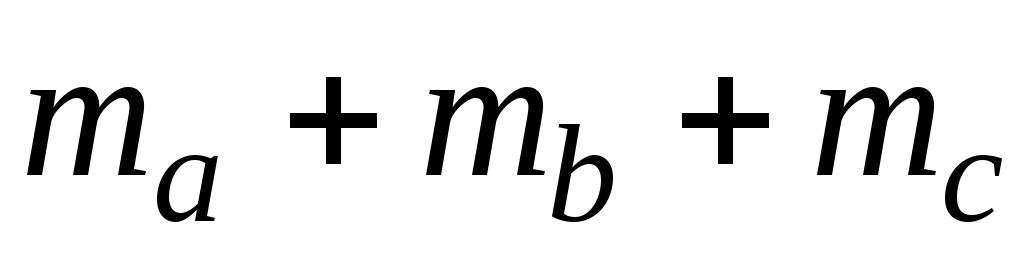, більшапериметра, але менша периметра.

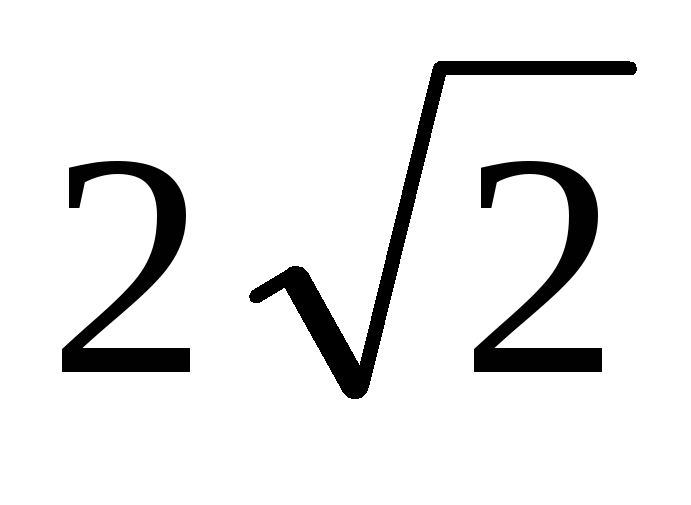20. Прямокутний трикутник з катетами ірозділений прямою, перпендикулярною гіпотенузі на дві рівновеликі частини. Знайти довжину відрізка цієї прямої, що міститься в середині трикутника.

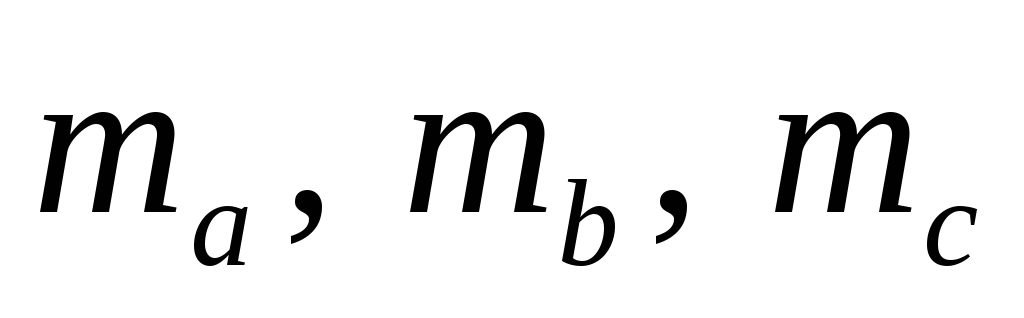21. Медіани трикутника задовольняють умові (- медіани трикутника). Визначити тип трикутника.

22. В трикутнику , такому, що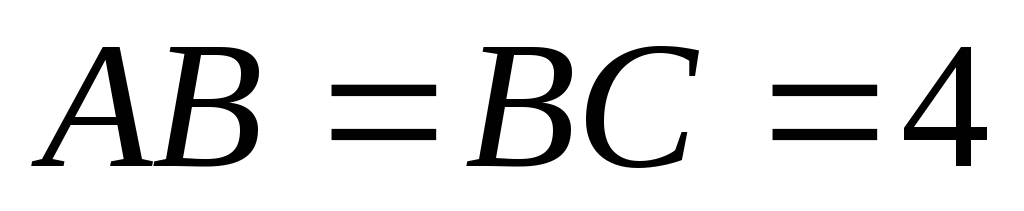см ісм, проведені бісектриса, медіанаі висота. Знайдіть площу трикутника, який утворено перетином прямих,і.

23. Площа трикутника АВС дорівнює 30 см². На стороні АС взята точка Д так, що АД/ДС = 2/3. Довжина перпендикуляра ДЕ, опущеного на сторону ВС, дорівнює 9 см. Знайти ВС.

24. Знайти суму квадратів медіан трикутника, якщо відомі довжини його сторін а, в, с.

25. Обчислити координати ортоцентра трикутника, заданого вершинами А (1; 2); В (3; -1); С (-1; 0) користуючись тільки формулою відстані між двома точками.

26. Дано прямокутний трикутник з катетами 3 м і 4 м. Проведено круг так, що його діаметр збігається з більшим катетом. Обчислити площі частин круга, на які він розбивається гіпотенузою трикутника.

27. У правильний чотирикутник вписано круг, а в нього вписано правильний п’ятикутник. Знайти відношення площ цих багатокутників.

28. У прямокутній трапеції висота дорівнює 6 м, на бічній стороні (не перпендикулярній до основ), як на діаметрі, побудовано коло так, що воно дотикається до протилежної сторони трапеції. Обчислити площу прямокутного трикутника, у якого катети дорівнюють основам трапеції.

29. Діагональ BD чотирикутника ABCD є діаметром описаного навколо нього кола. Знайти довжину діагоналі АС, якщо BD=2 м, АВ=1 м, кут ABD відноситься до кута DBC як 4 до 3.

30. Дано трапецію з основами а і b. Знайти довжину відрізка MN, який з’єднує бічні сторони трапеції і паралельний до основ та ділить площу трапеції навпіл.

31. Коло, проведене на основі AD трапеції ABCD як на діаметрі, проходить через середини бічних сторін АВ і СD трапеції та дотикається до основи ВС. Знайдіть кути трапеції.

32. У паралелограмі зі сторонами а і b і гострим кутом α проведені бісектриси чотирьох кутів. Знайти площу чотирикутника, вершинами якого служать точки перетину бісектрис.

33. З кінців сторони трикутника 10 см проведено дві медіани довжиною 9 см і 12 см. Знайти дві інші сторони трикутника.

34. Дано дві сторони трикутника а, с. Знайти третю сторону цього трикутника, якщо його площа дорівнює 0,4ас.

35. У коло вписано чотирикутник MNPQ, діагоналі якого взаємно перпендикулярні і перетинаються в точці F. Пряма, що проходить через точку F і середину сторони NP, перетинає сторону MQ в точці Н. Знайдіть кут між прямими FH та MQ.

36. У коло радіуса R вписано трикутник з кутами 15⁰ і 60⁰. Знайти площу цього трикутника.

37. Сума кутів при більшій основі трапеції дорівнює 90⁰. Основи трапеції рівні a та b. Знайти довжину відрізка, що сполучає середини основ трапеції.

38. Точка дотику кола вписаного в прямокутний трикутник ділить гіпотенузу на дві частини m і n. Знайти площу даного трикутника.

39. Діагоналі трапеції взаємно перпендикулярні, одна з них дорівнює 48см, а середня лінія трапеції – 25см. Знайдіть висоту трапеції.

40. Катети прямокутного трикутника дорівнюють 21см і 28см. Обчисліть площі частин трикутника, на які його ділить бісектриса прямого кута.

41. Бісектриса трикутника ділить сторону на відрізки 25см і 26см. Обчисліть відрізки, на які ділить цю сторону висота, довжина якої 72см.

42. Основа рівнобедреного трикутника дорівнює 36см, а бічна сторона – 54см. До бічних сторін трикутника проведено висоти. Обчисліть довжину відрізка, кінцями якого є основи висот.

43. Основа і бічна сторона рівнобедреного трикутника дорівнюють 20см і 30см відповідно. Знайдіть бісектрису кута при основі трикутника.

44. Діагональ рівнобічної трапеції ділить висоту, проведену з вершини тупого кута, на відрізки завдовжки 15см і 12см, а бічна сторона трапеції дорівнює її меншій основі. Знайдіть площу трапеції.

45. Катети прямокутного трикутника дорівнюють 6см і 8см. Знайдіть відстань від вершини меншого гострого кута трикутника до центра вписаного кола.

46. Основи рівнобічної трапеції дорівнюють 9см і 21см, а висота – 8см. Знайдіть радіус кола, описаного навколо даної трапеції.

47. Бісектриса кута А трикутника АВС (С=90) ділить катет ВС на відрізки завдовжки 6см і 10см. Знайдіть радіус кола, що проходить через точки А, С і точку перетину даної бісектриси з катетом ВС.

48. Центр кола, вписаного у прямокутну трапецію, віддалений від кінців її більшої бічної сторони на 15см і 20см. Обчисліть площу трапеції.

49. Катети прямокутного трикутника дорівнюють 18см і 24см. Знайдіть бісектрису трикутника, проведену з вершини меншого гострого кута.

50. Бічна сторона рівнобедреного трикутника дорівнює 4см, а медіана, проведена до цієї сторони, - 3см. Знайдіть периметр трикутника.

51. Діагональ рівнобічної трапеції перпендикулярна до бічної сторони і дорівнює 4см. Знайдіть площу трапеції, якщо радіус кола, описаного навколо неї, дорівнює 2,5см.

52. У рівнобедрений трикутник вписано коло, радіус якого дорівнює 10см, а точка дотику ділить бічну сторону на відрізки, довжини яких відносяться як 8:5, рахуючи від вершини рівнобедреного трикутника. Знайдіть площу цього трикутника.

53. Діагоналі рівнобічної трапеції є бісектрисами її гострих кутів і точкою перетину діляться у відношенні 5:13. знайдіть площу трапеції, якщо її висота дорівнює 9см.

54. Бісектриса кута А прямокутника АВСD ділить його сторону ВС на відрізки ВМ і МС завдовжки 10см і 14см відповідно. На відрізки якої довжини ця бісектриса ділить діагональ прямокутника?

55. Відрізок ВМ – медіана трикутника АВС, ВМ=m, АВМ=, МВС=. Знайдіть сторону АВ.

56. Центр кола, описаного навколо рівнобічної трапеції, лежить на її більшій основі. Знайдіть радіус цього кола, якщо діагональ трапеції дорівнює 20см, а її висота – 12см.

57. У трикутнику АВС АВ=ВС, ВD і АМ – висоти трикутника, ВD:АМ=3:1. знайдіть соsС.

58. Основи трапеції дорівнюють 2см і 6см, а бічні сторони – 13см і 15см. знайдіть площу трапеції.

59. У трикутнику АВС точка О – центр вписаного кола. Знайдіть радіус кола, описаного навколо цього трикутника, якщо АО=6см, ВО=10см, С=60.

60. Знайдіть радіус кола, описаного навколо рівнобічної трапеції, основи якої дорівнюють 11см і 21см, а бічна сторона – 13см.