Карта Карно на чотири змінних

Завдання. Знайти ДДНФ для формули .

Як звести формулу на три змінних до мінімальної форми вже всім відомо, а як бути з формулою на чотири змінних? Для таких формул користуються картою Карно на чотири змінних, яка має вигляд:

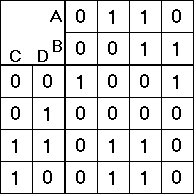
Заповнимо карту Карно на чотири змінних згідно ДДНФ формули останнього завдання. Тепер аналогічно карті Карно на три змінних потрібно знайти і виділити всі пари одиниць у таблиці, але одиниці у третьому рядку мають сусідами лише нулі, а одиниці у п’ятому і шостому рядках навпаки, мають поруч себе аж по дві одиниці. В таких випадках, коли чотири одиниці утворюють квадрат, можна виділяти весь квадрат, а коли одиниці розташовані в одному рядку(стовпчику) на протилежних сторонах карти Карно(неважливо на скільки зміннихкарта Карно), їх теж можна об’єднати у пару. Після виділення одиниць отримаємо:

Тепер об’єднуємо у один доданок виділену пару і у другий квадрат. У пари змінні А ,С і D є фіксованими імають значення нуль, а В не є фіксованою, тому цій парі відповідає доданок . У квадрата змінні А і С дорівнюють одиниці, тобто вони фіксовані, аB і D приймають різні значення і не є фіксованими, тому квадрату відповідає елементарна кон’юнкція АС. Отже .

Застосування алгебри логіки до теорії релейно-контактних схем.

Паралельні та послідовні з’єднання розмикаючих і замикаючих контактів називається релейно контактною схемою(РКС).

Є два типи контактів замикаючий і розмикаючий. Перший – контакт, який проводить струм коли його натискають, розмикаючий контакт, навпаки, проводить струм у не натиснутому стані.

ненатиснуті контакти

замикаючий(зараз схема розімкнута)

розмикаючий(зараз схема зімкнута)

натиснуті контакти

з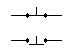амикаючий(зараз схема зімкнута)

розмикаючий(зараз схема розімкнута)

Але ми надалі будемо позначати їх так:

замикаючий контакт

розмикаючий контакт

послідовне з’єднання

паралельне з’єднання

Замикаючі контакти позначаємо Х, а розмикаючі , тобто в тому положенні, в якому вони пропускають струм.

Розглянемо таку просту РКС.

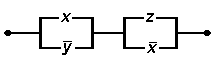
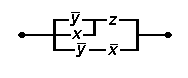Зауважимо, що перемикачі Хі не пропускають струм одночасно. Дана РКС проводить струм коли хоча б один з контактів Х або замкнутий і одночасно замкнутий хоча б один з контактів Zабо . Для отриманого висловлення(попереднього речення) будуємо схему, яка матиме вигляд:

У правій частині маємо рівносильну формулу, за якою можна скласти РКС, яка буде з’єднаною тоді і тільки тоді коли буде з’єднаною дана РКС.

Дуже часто доводиться мати справу з великими і громіздкими РКС, які потрібно спростити. Для цього складають логічну формулу, яка відповідає цій РКС, знаходять ДДНФ цієї формули і мінімізують її методом склеювання або за допомогою карт Карно. За мінімізованою ДДНФ будуємо нову РКС, яка зазвичай має менше перемикачів, ніж початкова.

„Те, що написано на початку цього розділу – безсовісна брехня”

1Наведене означення, як і ряд інших, не є строгим означенням, однак сподіваюся, що воно буде зрозумілим читачу.