
- •§1. Алгебраїчні структури з однією операцією. Означення групи, найпростіші властивості груп.
- •IV. Деякі інші означення групи
- •2. Підгрупи. Циклічні групи.
- •§1. Означення кільця, властивості та основні поняття. Приклади кілець.
- •2.Гомоморфізми та ізоморфізми кілець
- •§ 3. Ідеали кілець.
- •1.Означення ідеалу кільця, приклади ідеалів.
- •2. Кільця головних ідеалів та евклідові кільця.
- •§5. Конгруенції та фактор кільця за ідеалом.
- •2.Фактор-кільця комутативного кільця за ідеалом і.
- •3. Фактор-кільця і гомоморфізми.
- •4. Конгруенції за модулем
- •§6. Класи лишків кільця цілих чисел за модулем .
- •1.Конгруенції та класи лишків за модулем
- •2. Кільце класів лишків за модулем .
- •§7 Деякі арифметичні застосування теорії конгруенцій
- •1. Застосування конгруенцій до встановлення ознак подільності.
- •2. Перетворення звичайного дробу в систематичний і визначення довжини періоду систематичного дробу.
3. Фактор-кільця і гомоморфізми.
Встановимо зв’язок між поняттям фактор-кільця і поняттям гомоморфізму кільця.
Нехай
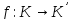 гомоморфізм кільцяК
в кільці К′.
В §3 показано, що ядро Kerfцього
гомоморфізму є ідеалом кільця К.
Тому можна говорити про фактор-кільце
К/Kerf
кільця К
за ядром гомоморфізму
гомоморфізм кільцяК
в кільці К′.
В §3 показано, що ядро Kerfцього
гомоморфізму є ідеалом кільця К.
Тому можна говорити про фактор-кільце
К/Kerf
кільця К
за ядром гомоморфізму
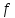 .
Як бачимо, кожен гомоморфізм визначає
деяке фактор-кільце.
.
Як бачимо, кожен гомоморфізм визначає
деяке фактор-кільце.
Виявляється,
що і навпаки: якщо дано фактор-кільце
К⁄І,
поставивши
у відповідність кожному елементу а Ксуміжний
клас а+І.
Цей
епіморфізм
х: К→К⁄І, ядром
якого служить ідеал І.
Цей
епіморфізм називається канонічним
гомоморфізмом. Гомоморфність так
заданого відображення показується так:
Ксуміжний
клас а+І.
Цей
епіморфізм
х: К→К⁄І, ядром
якого служить ідеал І.
Цей
епіморфізм називається канонічним
гомоморфізмом. Гомоморфність так
заданого відображення показується так:
 а,b
а,b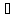 K:x(a)=a+I,
x(b)=b+I,
K:x(a)=a+I,
x(b)=b+I,
Тоді
x(a+b)=(a+b)+ I=(a+I)+(b+I)=x(a)+x(b),
x(ab)=ab+ I=(a+I)(b+I)=x(a)x(b).
Теорема
5.
(про гомоморфізми) Для всякого епіморфізму
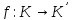 існує
однозначно означений гомоморфізм
кільця К∕Ker
на кільце К′ такий, що епіморфізм
існує
однозначно означений гомоморфізм
кільця К∕Ker
на кільце К′ такий, що епіморфізм
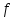 є результатом послідовного застосування
канонічного гомоморфізмуx:
К→К∕Kerf,
а
потім
є результатом послідовного застосування
канонічного гомоморфізмуx:
К→К∕Kerf,
а
потім
4. Конгруенції за модулем
Якщо
K - область цілісності з І і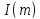 - головний ідеал, породжений елементом
- головний ідеал, породжений елементом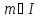 ,
то всякі елементи
,
то всякі елементи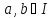 , які конгруентні за ідеалом
, які конгруентні за ідеалом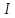 , називають конгруентними за модулем
, називають конгруентними за модулем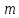 і записують, це так:
і записують, це так:
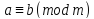
Суміжні
класи кільця K - за ідеалом і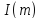 називають в даному випадку суміжними
класами за модулем
називають в даному випадку суміжними
класами за модулем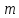 .
Будь-який елемент суміжного класу
називають часто лишком цього класу.
Тому суміжні класи за модулем
.
Будь-який елемент суміжного класу
називають часто лишком цього класу.
Тому суміжні класи за модулем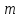 часто називають класами лишків за
модулем
часто називають класами лишків за
модулем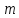 .
.
Теорема
7.
Елементи
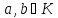 конгруентні між собою за модулем
конгруентні між собою за модулем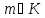 тоді і тільки тоді, коли
тоді і тільки тоді, коли
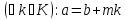
Доведення.
Якщо
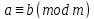 ,
то
,
то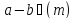 тобто
тобто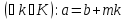 навпаки, якщо
навпаки, якщо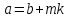 ,
то
,
то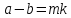 ,тобто,
,тобто,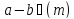 і,значить,
і,значить,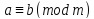 . Відзначимо деякі властивості конгруенцій
за модулем
. Відзначимо деякі властивості конгруенцій
за модулем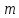 .
Основні властивості конгруенцій
сформульовані в теоремі І. Із цієї
теореми випливає, зокрема, що почленне
додавання і множення конгруенцій за
одним і тим же модулем не приводить до
порушення конгруентності. Конгруентність
не порушується ще й при таких перетвореннях:
.
Основні властивості конгруенцій
сформульовані в теоремі І. Із цієї
теореми випливає, зокрема, що почленне
додавання і множення конгруенцій за
одним і тим же модулем не приводить до
порушення конгруентності. Конгруентність
не порушується ще й при таких перетвореннях:
додавання до обох частин конгруенції одного і того ж елемента;
перенесення з протилежним знаком будь-якого доданка з однієї частини конгруенції в другу;
додавання до однієї частини конгруенції елемента, кратного модулю;
множення обох частин конгруенції на будь-який елемент;
ділення обох частин конгруенції на їх спільний дільник, що взаємно простий з модулем;
множення обох частин конгруенції і модуля на довільний елемент;
ділення обох частин конгруенції і модуля на їх довільний спільний дільник.
Доведення непорушності конгруентності при вказаних перетвореннях
тривіальне і проводиться цілком аналогічно, як і для цілих чисел
(див. наприклад, О.І.Бородін, Теорія чисел, §15).
Вкажемо ще одну просту і важливу властивість конгруенцій.
Якщо
елементи
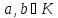 конгруентні за модулем
конгруентні за модулем ,
то вони конгруентні і за їх найменшим
спільним
кратним
,
то вони конгруентні і за їх найменшим
спільним
кратним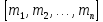
Справді,
із конгруенцій
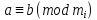 випливає
випливає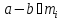 , тобто
, тобто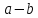 є спільним кратним чисел
є спільним кратним чисел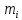 і, значить, елемент
і, значить, елемент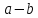 ділиться
ділиться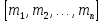 ,
звідки випливає потрібна конгруенції
,
звідки випливає потрібна конгруенції
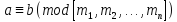 .
.
§6. Класи лишків кільця цілих чисел за модулем .
1.Конгруенції та класи лишків за модулем
В цьому параграфі застосуємо результати попереднього параграфу до кільця цілих чисел.
Насамперед
зауважимо, що, як це показано в §2, кільце
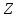 цілих чисел є кільцем головних ідеалів
- всякий ненульовий ідеал в
цілих чисел є кільцем головних ідеалів
- всякий ненульовий ідеал в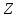 є сукупністю чисел, кратних деякому
натуральному числу
є сукупністю чисел, кратних деякому
натуральному числу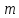 ,
його можна записувати у вигляд
,
його можна записувати у вигляд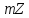 .
Тому конгруенції в цьому кільці є
конгруенціями за модулем
.
Тому конгруенції в цьому кільці є
конгруенціями за модулем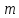 , Нагадаємо, що за означенням числа
, Нагадаємо, що за означенням числа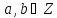 конгруентні за модулем
конгруентні за модулем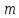 , якщо їх різниця
, якщо їх різниця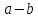 ділиться націло на
ділиться націло на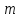 .
За теоремою 3 §5 числа
.
За теоремою 3 §5 числа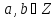 конгруентні за
конгруентні за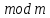 тоді і тільки тоді, коли існує
тоді і тільки тоді, коли існує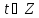 таке, що
таке, що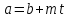 .
Для цілих чисел справедливий ще один
критерій конгруентності.
.
Для цілих чисел справедливий ще один
критерій конгруентності.
Теорема
1.
Цілі числа a і b конгруентні за модулем
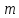 тоді і тільки тоді, коли вони мають
однакові остачі при діленні на
тоді і тільки тоді, коли вони мають
однакові остачі при діленні на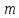 .
.
Доведення. За теоремою про ділення з остачею
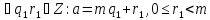
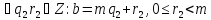
Звідки
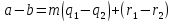 .
Оскільки перший доданок даної суми
ділиться на
.
Оскільки перший доданок даної суми
ділиться на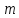 , то вся сума ділиться на
, то вся сума ділиться на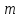 тоді і тільки тоді,коли на
тоді і тільки тоді,коли на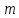 ділиться другий доданок
ділиться другий доданок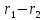 .
Останнє, внаслідок того,
.
Останнє, внаслідок того,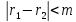 можливе тоді і тільки тоді, коли
можливе тоді і тільки тоді, коли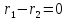 ,
тобто
,
тобто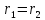 .
.
З
теореми 2 §5 випливає, що сукупність
чисел, конгруентних між собою за
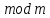 ,
співпадає з деяким суміжним класом
кільця
,
співпадає з деяким суміжним класом
кільця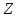 за ідеалом
за ідеалом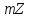 .
Через це сукупність чисел, конгруентних
між собою за
.
Через це сукупність чисел, конгруентних
між собою за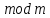 , називається класом чисел,конгруентних
за
, називається класом чисел,конгруентних
за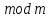 ,
а будь-яке число із цього класу його
представником або лишком. Тому клас
чисел,конгруентних за модулем
,
а будь-яке число із цього класу його
представником або лишком. Тому клас
чисел,конгруентних за модулем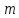 ще називають класом лишків кільця
цілих чисел за модулем
ще називають класом лишків кільця
цілих чисел за модулем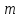 .
.
Як
відомо, сукупність суміжних класів
кільця K за ідеалом
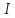 утворює розбиття цього кільця, яке само
є кільцем відносно операцій додавання
та множення класів - фактор-кільцем K/
утворює розбиття цього кільця, яке само
є кільцем відносно операцій додавання
та множення класів - фактор-кільцем K/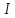 ,
Тому сукупність класів лишків кільця
цілих чисел за модулем
,
Тому сукупність класів лишків кільця
цілих чисел за модулем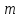 утворює фактор-кільце
утворює фактор-кільце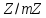 .
З теореми І виходить, що фактор-кільце
.
З теореми І виходить, що фактор-кільце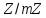 є скінченим і містить
є скінченим і містить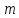 різних класів.
різних класів.
Справді,
кожен клас лишків
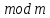 є сукупність всіх цілих чисел, що при
діленні на
є сукупність всіх цілих чисел, що при
діленні на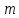 дають одну і ту ж остачу
дають одну і ту ж остачу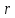 .
Оскільки всіх остач є
.
Оскільки всіх остач є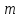 - 0,1,2,...,
- 0,1,2,...,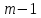 — кожна з них міститься в одному і тільки
в одному класі лишків та, навпаки, кожен
клас містить одну з цих остач, то всіх
різних класів лишків є
— кожна з них міститься в одному і тільки
в одному класі лишків та, навпаки, кожен
клас містить одну з цих остач, то всіх
різних класів лишків є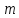 .
.
Класи
лишків за модулем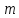 позначають часто через
позначають часто через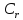 ,
де
,
де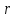 —
остача чисел даного класу при діленні
на
—
остача чисел даного класу при діленні
на
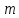 .
Випишемо їх:
.
Випишемо їх:
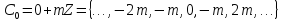
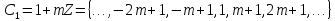
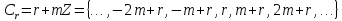
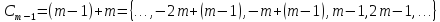
Якщо
з кожного класу чисел за модулем
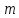 взяти по одному і тільки, по одному
лишку, то одержана система чисел
називається повною системою лишків
модулем
взяти по одному і тільки, по одному
лишку, то одержана система чисел
називається повною системою лишків
модулем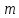 . Найчастіше за повну систему лишків за
модулем
. Найчастіше за повну систему лишків за
модулем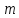 вибирають найменші невід’ємні лишки
0,1,2,...,
вибирають найменші невід’ємні лишки
0,1,2,...,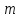 або абсолютно найменші лишки, тобто
лишки, які в своїх класах є найменшими
за абсолютною величиною. За модулем 10,
наприклад, повною системою найменших
невід'ємних лишків є:
або абсолютно найменші лишки, тобто
лишки, які в своїх класах є найменшими
за абсолютною величиною. За модулем 10,
наприклад, повною системою найменших
невід'ємних лишків є:
0,1,2,3,4,5,6,7,8,9,
а повною системою абсолютно найменших лишків є
0,1,2,3,4,5,-4,-3,-2,-1
Або
0,1,2,3,4,-5,-4,-3,-2,-1.
Крім повних систем лишків, в теорії
чисел важливу роль відіграють так звані
зведені системи лишків. Щоб підійти до
цього поняття, зауважимо, що числа одного
і того ж класу
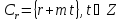 в силу відомого співвідношення
в силу відомого співвідношення
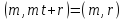
Мають
модулем один і той же найбільший спільний
дільник. Зокрема, всі числа одного і
того ж класу
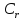 є одночасно взаємно простими з
є одночасно взаємно простими з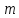 або взаємно не простими з
або взаємно не простими з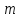 ,
тобто можна говорити про класи чисел,
взаємно простих а модулем
,
тобто можна говорити про класи чисел,
взаємно простих а модулем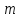 .
При цьому клас
.
При цьому клас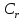 є взаємно простим за модулем
є взаємно простим за модулем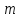 тоді і тільки тоді, Коли
тоді і тільки тоді, Коли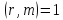 .
Це означає, що класів чисел, взаємно
простих з модулем
.
Це означає, що класів чисел, взаємно
простих з модулем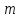 ,
є стільки, скільки є чисел, меиших від
,
є стільки, скільки є чисел, меиших від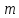 і взаємно простих
і взаємно простих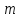 ,
тобто,
,
тобто,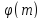 .
Явдо з кожного класу лишків, взаємно
простих за модулем
.
Явдо з кожного класу лишків, взаємно
простих за модулем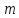 ,
взяти по одному і тільки по одному лишку,
то одержана сукупність чисел називається
зведеною системою лишків за модулем
,
взяти по одному і тільки по одному лишку,
то одержана сукупність чисел називається
зведеною системою лишків за модулем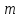 .
Щоб зведену систему, треба з повної
системи ликів за модулем
.
Щоб зведену систему, треба з повної
системи ликів за модулем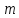 вибрити числа, взаємно прості з
вибрити числа, взаємно прості з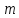 .
.
