
- •§1. Алгебраїчні структури з однією операцією. Означення групи, найпростіші властивості груп.
- •IV. Деякі інші означення групи
- •2. Підгрупи. Циклічні групи.
- •§1. Означення кільця, властивості та основні поняття. Приклади кілець.
- •2.Гомоморфізми та ізоморфізми кілець
- •§ 3. Ідеали кілець.
- •1.Означення ідеалу кільця, приклади ідеалів.
- •2. Кільця головних ідеалів та евклідові кільця.
- •§5. Конгруенції та фактор кільця за ідеалом.
- •2.Фактор-кільця комутативного кільця за ідеалом і.
- •3. Фактор-кільця і гомоморфізми.
- •4. Конгруенції за модулем
- •§6. Класи лишків кільця цілих чисел за модулем .
- •1.Конгруенції та класи лишків за модулем
- •2. Кільце класів лишків за модулем .
- •§7 Деякі арифметичні застосування теорії конгруенцій
- •1. Застосування конгруенцій до встановлення ознак подільності.
- •2. Перетворення звичайного дробу в систематичний і визначення довжини періоду систематичного дробу.
§5. Конгруенції та фактор кільця за ідеалом.
Конгруенції комутативного кільця К за ідеалам І.
Крім алгебраїчних операцій в кільці К можуть бути введені і деякі інші відношення, зокрема, відношення еквівалентності. З алгебраїчної точки зору інтерес представляють тільки такі відношення еквівалентності, які певним способом узгодженні з операціями, означеними в кільці.
Означення. Говорять, що відношення еквівалентності ab в комутативному кільці К узгоджено з алгебраїчними операціями цього кільця, якщо:
(a, b, c, dє К):(ab)(c d)(a + c b + d)(ac bd)
Прикладом відношення еквівалентності, узгодженого з операціями кільця, служить відношення конгруентності за модулем ідеалу.
Означення.
Говорять, що елементи a,
b
комутативного кільця конгруентні між
собою, за ідеалом ІК
і за модулем ідеалу І,
якщо a
- b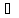 І,
і записується це так:
І,
і записується це так:
a b(modI)
Теорема 1. Відношення конгруентності за ідеалом І кільця К відношенням еквівалентності в К, узгодженим з операціями К.
Доведення. Оскільки кожен ідеал І кільця К є підкільцем, отже, і підгрупою групи цього кільця, то перевірка того, що відношення конгруентності за ідеалом І є відношення еквівалентності. Узгодженим з операцією додавання, приводиться точно так, як і в теорії груп. І тому зараз проводити її не будемо. Покажемо тільки, що коли
a b(mod I), c d(mod I), /1/
то ac bd(mod I) /2/
з цією метою розглянемо різницю ac – bd
ac-bd=(ac – bd) + (bc – bd) = (a-b)c +b(c-d) /3/
в
силу конгруенції /1/ a-b,
c-d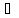 І.
тоді за другою умовою з означення ідеалу
(a-b)c,
b(c-d)
І.
тоді за другою умовою з означення ідеалу
(a-b)c,
b(c-d)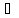 І,
внаслідок того, що ідеал є підкільцем
(a-b)c
+b(c-d)
І,
внаслідок того, що ідеал є підкільцем
(a-b)c
+b(c-d)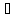 І,
що рівносильна конгруенції /2/. Теорема
доведена.
І,
що рівносильна конгруенції /2/. Теорема
доведена.
Виявляється, що відношення конгруентності за ідеалом І вичерпуються усі відношення еквівалентності, узгодженні з операціями кільця. Точніше справедлива теорема 2.
Теорема 2. Для всякого відношення еквівалентності в кільця К, узгодженого з операціями цього кільця, існує ідеал І такий, що дане відношення еквівалентності є відношення конгруентності за ідеалом І.
Доведення цієї теореми проводити не будемо.
2.Фактор-кільця комутативного кільця за ідеалом і.
Добре відомо, що всяке відношення еквівалентності на множені І породжує розбитя цієї множини на класи, класи еквівалентності. Та відношення конгруентності за модулем ідеалу І в кільці К породжує розбиття кільця К на класи. Ці класи називають суміжними класами або класами елементів. Конгруентних за ідеалом І.
ОзначенняСуміжним
класом комутативного кільця К
за ідеалом або класу елементів,
конгруентних за ідеалом І
кільця К
називають всякий клас еквівалентності
відношенням конгруентності за ідеалом
І,
тобто. Сукупність Са
усіх елементів кільця К,
які конгруентні елементу а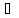 К,
і значить конгруентні між собою за
ідеалом І.
К,
і значить конгруентні між собою за
ідеалом І.
Як уже відзначалося, кожен ідеал І кільця К є підгрупою адитивної групи кільця К і, значить, відношення конгруентної в кільці К за ідеалом І є відношенням конгруентності в адитивній групі кільця К за підгрупою І, а кожен суміжний клас кільця К за ідеалом І є суміжним класом адитивної групи кільця К за підгрупою І. Тому суміжні класи кільця К за ідеалом І мають таку ж структуру, як і суміжні класи адитивної абелевої групи за підгрупою, тобто, справедлива така теорема.
Теорема 3. Всякий суміжний клас Са комутативного кільця К за ідеалом І можна подати у вигляді Са= а + І, де а — довільний елемент класу Са. Навпаки, всяка множина а + І, де а — довільний елемент кільця К, утворює суміжний клас кільця К за ідеалом І.
Нагадаємо, що за означенням
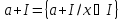
Розглянемо сукупність К/І усіх суміжних класів комутативного кільця К за ідеалом І
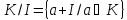
Як відомо, у випадку адитивної абелевої групи ця сукупність утворює групу, так звану фактор-групу. У випадку кільця сукупність К/І є кільцем.
Теорема 4. Сукупність К/І усіх суміжних класів комутативного кільця К за ідеалом І є комутативним кільцем. Якщо кільце К містить І, то і кільце К/І містить одиницю.
Кільце К/І називають фактор-кільцем кільця К за ідеалом І.
Доведення. Сукупність К/І можна розглядати як сукупність суміжних класів адитивної групи кільця К за підгрупою І, а така сукупність, як відомо з теорії груп, утворює адитивну абелеву групу, фактор-групу групи К за підгрупою І, причому операція додавання задається формулою:
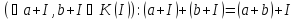
Тому для завершення доведення теореми треба тільки ввести у множині К/І операцію множення і перевірити, що вона є асоціативною, комутативною і пов’язана з додаванням дистрибутивним законом.
Операцію множення суміжних класів задамо так:
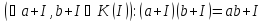
Покажемо, що так означене множення є однозначне, тобто, що за формулою у відповідність суміжним класам а+І та b+І ставиться єдиний суміжний клас ab+І. Неоднозначність може виникнути за рахунок того, що в поданні суміжного класу у виді а+І елемент а є довільним елементом цього класу. Значить, якщо
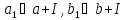 ,
то
,
то
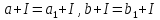 .
.
Тоді
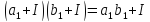 і щоб множення було однозначним, має
бути справедлива рівність
і щоб множення було однозначним, має
бути справедлива рівність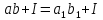 .
.
Доведемо, що це насправді так.
Належності
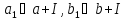 ,
означають, що
,
означають, що
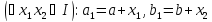
Тоді
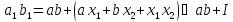 звідки виходить, що класиав+І
і а1в1+І
мають спільний елемент а1в1,і
тому вони співпадають:
звідки виходить, що класиав+І
і а1в1+І
мають спільний елемент а1в1,і
тому вони співпадають:
аb+І = а1b1+І
Цим однозначність множення доведена.
Асоціативність множення класів випливає із асоціативності множення в К:
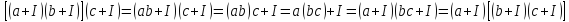 .
.
Аналогічно доводиться комутативність множення класів. Так само аналогічно виводиться дистрибутивність:
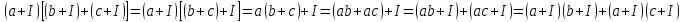 .
.
Якщо в кільці К є одиниця, то, очевидно клас 1+І — одиниця фактор-кільця К/І.
