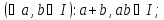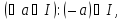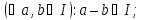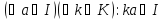- •§1. Алгебраїчні структури з однією операцією. Означення групи, найпростіші властивості груп.
- •IV. Деякі інші означення групи
- •2. Підгрупи. Циклічні групи.
- •§1. Означення кільця, властивості та основні поняття. Приклади кілець.
- •2.Гомоморфізми та ізоморфізми кілець
- •§ 3. Ідеали кілець.
- •1.Означення ідеалу кільця, приклади ідеалів.
- •2. Кільця головних ідеалів та евклідові кільця.
- •§5. Конгруенції та фактор кільця за ідеалом.
- •2.Фактор-кільця комутативного кільця за ідеалом і.
- •3. Фактор-кільця і гомоморфізми.
- •4. Конгруенції за модулем
- •§6. Класи лишків кільця цілих чисел за модулем .
- •1.Конгруенції та класи лишків за модулем
- •2. Кільце класів лишків за модулем .
- •§7 Деякі арифметичні застосування теорії конгруенцій
- •1. Застосування конгруенцій до встановлення ознак подільності.
- •2. Перетворення звичайного дробу в систематичний і визначення довжини періоду систематичного дробу.
§ 3. Ідеали кілець.
1.Означення ідеалу кільця, приклади ідеалів.
Серед усіх підмножин кільця К особливу роль відіграють ті, які містять усі різниці своїх елементів та усі добутки своїх елементів з довільними елементами кільця. Такі підмножини кільця називаються його ідеалами.
Означення. Підмножина І кільця К називається його ідеалом, якщо
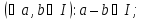
(
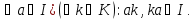
Теорема 1.Всякий ідеал І кільця К є підкільцем цього кільця.
Доведення За означенням ідеалу
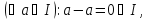
тобто нуль кільця К належить ідеалу І.
Тоді
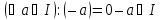 і,
значить,
і,
значить,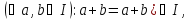
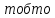 ,
сума будь-яких двох елементів з І належить
І. За другою умовою з означення ідеалу
,
сума будь-яких двох елементів з І належить
І. За другою умовою з означення ідеалу
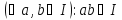
Отже,
а виконання цих умов достатнє для того, щоб підмножина кільця була підкільцем. Таким чином, І — підкільце кільця К.
Оскільки операція множення не в кожному кільці комутативна, то часто доводиться розглядати односторонні ідеали — лівосторонні, якщо
та правосторонні, якщо
1)
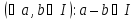
2)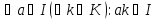
Через це ідеали в розумінні означення І називають двосторонніми.
Приклади:
Множина всіх цілих чисел, кратних натуральному числу n, є ідеалом кільця Z цілих чисел.
Сукупність усіх квадратних матриць n-го порядку, в яких останній стовпець складаються з нулів, утворює лівосторонній ідеал в кільці
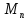 квадратних матрицьn-го
порядку над числовим полем Р.
квадратних матрицьn-го
порядку над числовим полем Р.
Виділимо деякі типи ідеалів комутативного кільця К з одиницею.
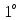 Підмножина
О = {0}
кільця
К,
яка складається тільки з одного нуля,
є ідеалом, так званим нульовим ідеалом.
Все кільце К
теж є ідеалом самого себе і називається
одиничним ідеалом.
Підмножина
О = {0}
кільця
К,
яка складається тільки з одного нуля,
є ідеалом, так званим нульовим ідеалом.
Все кільце К
теж є ідеалом самого себе і називається
одиничним ідеалом.
ЦіідеалиназиваютьсятривіальнимиабоідеаламикільцяК.
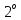 Якщоa—
деякийелементК,
то множина(а)={ak
|k
є К}
Якщоa—
деякийелементК,
то множина(а)={ak
|k
є К}
єідеаломкільцяК , якимназиваєтьсяголовнимідеаломкільцяК, породженимелементома.
Доведенняочевидне.
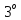 .
Нехай,
.
Нехай,
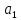 ,
,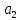 ,
…….
,
…….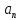 .
деякі елементи кільцяК.
Тодімножина
.
деякі елементи кільцяК.
Тодімножина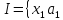 +
+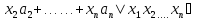 K}
є ідеалом.
K}
є ідеалом.
Справді, операціядодавання в кільцікомутативна, асоціативна, зв’язана з множенням, дистрибутивним законом та, крім того,
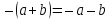 i
i 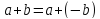
Тому
1/
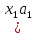 +
+ )-
)-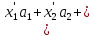 ……+
……+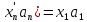 +
+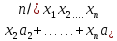 +
+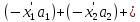 ……+(
……+(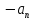 )
= [
)
= [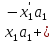 )]+[
)]+[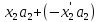 ]+………+[
]+………+[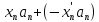 ]
= (
]
= (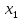 -
-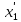 )
)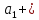 …….+(
…….+( -
-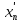 )
)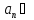 I
I
2/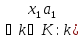 +
+ )
=(k
)
=(k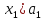 +…..+
+…..+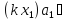 І
І
Отже, Ізадовольняєобомумовам з означенняідеалуІ, значить , є ідеалом .
Цейідеалназиваєтьсяідеалом,
породженимелементами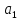 ,
,
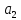 ,
…….
,
…….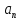
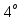 .
.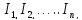 - деякі елементи кільця К
. Тоді множина
- деякі елементи кільця К
. Тоді множина
І=
{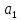 +
+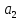 +
……
+
……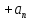 /
/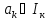 ,k=1,2,…..n
}
,k=1,2,…..n
}
Утворюєідеал,
котрийназивається
сумою ідеалів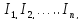
Доведенняаналогічне
до
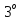
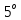 .Якщо
.Якщо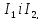 - ідеаликільцяК,
то їхперетин—тежідеал.
- ідеаликільцяК,
то їхперетин—тежідеал.
Дійсно,
якщо
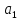 ,
,
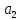 є
є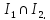 то
то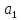 ,
,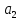 є
є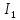 /
/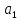 ,
,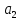 є
є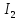 Оскільки
Оскільки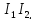 -ідеали,
то
-ідеали,
то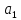 ,
,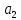 є
є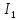 /
/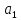 ,
,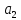 є
є .
Тому
.
Тому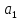 ,
,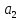 є
є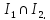 Аналогічно перевіряється друга умова
з означення ідеалу.
Аналогічно перевіряється друга умова
з означення ідеалу.
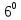 .
Нехай
.
Нехай
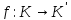 –гомоморфізм
з кільця
–гомоморфізм
з кільця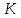 в
кільце
в
кільце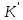 .
Тому його ядро
.
Тому його ядро
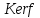 є ідеалом кільця
є ідеалом кільця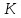
Справді,
якщо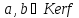 то
то
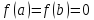 і тому
і тому
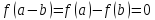
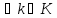 :
: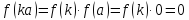 ,
,
тобто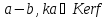
Кільце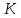 ,
в якому не існує нетривіальних двосторонніх
ідеалів називається простим.
,
в якому не існує нетривіальних двосторонніх
ідеалів називається простим.
Приклади:
1)Кільце
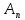 всіх матриць
всіх матриць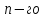 порядку над полем є простим.
порядку над полем є простим.
Щоб
довести це,
треба показати,
що
коли
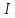 – деякий ненульовий ідеал кільця
– деякий ненульовий ідеал кільця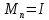 .
Оскільки
.
Оскільки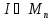 ,
то залишається довести, що всяка матриця
із
,
то залишається довести, що всяка матриця
із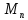 належить
належить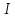 .
Внаслідок того, що всяку матрицю
.
Внаслідок того, що всяку матрицю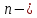 го
порядку можна подати у вигляді суми
го
порядку можна подати у вигляді суми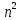 матриць,
в яких хіба що тільки один елемент не
дорівнює
0, і всякий ідеал
є підкільцем, тобто, разом із скінченною
кількістю своїх елементів містить і їх
суму, для доведення включення досить
показати, що ідеалу
матриць,
в яких хіба що тільки один елемент не
дорівнює
0, і всякий ідеал
є підкільцем, тобто, разом із скінченною
кількістю своїх елементів містить і їх
суму, для доведення включення досить
показати, що ідеалу
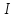 належать всі матрицііз
належать всі матрицііз
 , в яких тільки один елемент не дорівнює
0.
, в яких тільки один елемент не дорівнює
0.
Отже,
нехай
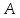 – деяка матриця
– деяка матриця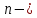 го
порядку, в якої всі елементи, крім
го
порядку, в якої всі елементи, крім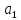 ,
дорівнюють 0, а
,
дорівнюють 0, а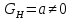 .
Оскільки
.
Оскільки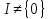 ,
то в
,
то в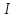 існує матриця
існує матриця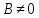 , в котрій деякий елемент
, в котрій деякий елемент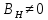 .
Розглянемо матрицю
.
Розглянемо матрицю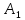 ,
в якої всі елементи, крім
,
в якої всі елементи, крім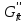 ,
дорівнюють теж 0, а елементи
,
дорівнюють теж 0, а елементи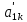 і
і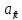 підібрані так, що
підібрані так, що
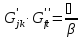
Легко
бачити, що тоді
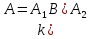 В силу другої умови з означення ідеалу
В силу другої умови з означення ідеалу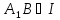 і
і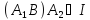 .
Томуматриця
.
Томуматриця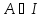 .
Яквжевідзначалося, зцьоговиходить, що
.
Яквжевідзначалося, зцьоговиходить, що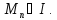
2)
Всяке поле
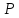 є простим кільцем.
є простим кільцем.
Справді,
нехай
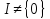 – довільний ідеал поля
– довільний ідеал поля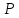 і
і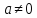 —
довільний його елемент. Тоді існує
—
довільний його елемент. Тоді існує
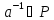 і згідно з другою властивістю з означення
ідеалу:
і згідно з другою властивістю з означення
ідеалу:
Звідси на підставі цієї ж другої умови

тобто
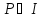 і, значить,
і, значить,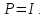
Відсутність нетривіальних ідеалів — характерна властивість полів.