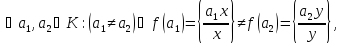- •§1. Алгебраїчні структури з однією операцією. Означення групи, найпростіші властивості груп.
- •IV. Деякі інші означення групи
- •2. Підгрупи. Циклічні групи.
- •§1. Означення кільця, властивості та основні поняття. Приклади кілець.
- •2.Гомоморфізми та ізоморфізми кілець
- •§ 3. Ідеали кілець.
- •1.Означення ідеалу кільця, приклади ідеалів.
- •2. Кільця головних ідеалів та евклідові кільця.
- •§5. Конгруенції та фактор кільця за ідеалом.
- •2.Фактор-кільця комутативного кільця за ідеалом і.
- •3. Фактор-кільця і гомоморфізми.
- •4. Конгруенції за модулем
- •§6. Класи лишків кільця цілих чисел за модулем .
- •1.Конгруенції та класи лишків за модулем
- •2. Кільце класів лишків за модулем .
- •§7 Деякі арифметичні застосування теорії конгруенцій
- •1. Застосування конгруенцій до встановлення ознак подільності.
- •2. Перетворення звичайного дробу в систематичний і визначення довжини періоду систематичного дробу.
2.Гомоморфізми та ізоморфізми кілець
1.Як
відомо, одним із основних понять
математики є поняття, функції, відображення.
Це поняття вивчається і в математичному
аналізі,і в геометрії,і в алгебрі. При
вивченні алгебраїчних структур найбільший
інтерес становлять ті відображення,
які певним способом узгодженні із
алгебраїчною структурою, що вивчається.
В теорії груп такими відображеннями є
гомоморфізми, тобто, такі ж відображення
f
групи G
в групу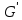 що
що
(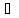 а,b
а,b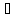 G):
f(ab)=f(a)
G):
f(ab)=f(a)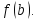
В теорії кілець вивчаються відображення, які аналогічним способом узгоджені з алгебраїчними операціями, означеними в кільці. Такі відображення називаються кільцевими гомоморфізмами.
Означення
1.Відображення
fкільця
К
в кільце
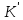 називається
гомоморфізмом, якщо
називається
гомоморфізмом, якщо
( а,b
а,b К):
f(a+b)=f(a)+f(b),
f(ab)=f(a)f(b).
К):
f(a+b)=f(a)+f(b),
f(ab)=f(a)f(b).
Перша
з цих умов означає, що кільцевий
гомоморфізм f
в
груповим гомоморфізмом адитивної групи
кільця К
в
адитивну групу кільця
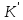 .
Внаслідок цього всі властивості групових
гомоморфізмів справедливі і для кільцевих
гомоморфізмів. Зокрема:
.
Внаслідок цього всі властивості групових
гомоморфізмів справедливі і для кільцевих
гомоморфізмів. Зокрема:
1.f(o)=0;
2.(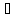 а,
а,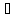 К):f(-a)=-f(a)
К):f(-a)=-f(a)
Аналогічно,
як і випадку груп, гомоморфізм f:
K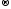
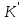 ,
який ін’єктивним відображенням,
називається
мономорфізмом: гомоморфізм
f:
K
,
який ін’єктивним відображенням,
називається
мономорфізмом: гомоморфізм
f:
K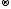
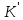 ,
який є сур’єктивним відображенням,
називається епіморфізмом:
гомоморфізм f:
K
,
який є сур’єктивним відображенням,
називається епіморфізмом:
гомоморфізм f:
K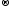
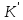 ,
який є бієктивним відображенням,
називається ізоморфізмом.
,
який є бієктивним відображенням,
називається ізоморфізмом.
У зв’язку із властивостями 1. i 2. Виникає питання, чи не будуть аналогічні властивості справедливі відносно операцій множення. Виявляється, що будуть, але при деяких обмеженнях на кільця або на відображення f. Сформулюємо їх:
3.
Якщо в кільці К
існує 1 if
є епіморфізмом кільця К
в кільці
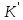 ,
то вкільці
,
то вкільці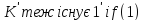 =
=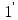 .
.
Справді, внаслідок сур’єктивності відображення f:
(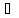 а
а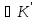 )
(
)
(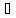 а
а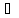 К):
К):
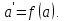
Тоді
(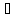 а
а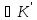 ):
):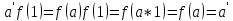
(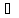 а
а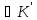 ):f(1)
):f(1)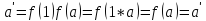
Звідси
виходить, що елемент f(1)
відіграє роль одиниці в кільці
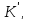 тобтоf(1)=
тобтоf(1)=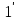 .Зауважимо,
що одиничні елементи в кільцях К
і
.Зауважимо,
що одиничні елементи в кільцях К
і
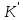 є
єдиними.
є
єдиними.
4.Якщо
в кільці К існує І, кільце
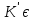 областю
цілісності з одиницею
областю
цілісності з одиницею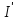 ,
то для всякого гомоморфізмуf:
K
,
то для всякого гомоморфізмуf:
K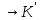 справедливо
f(1)=
справедливо
f(1)=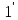 .
.
Дісно,
(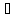 а
а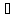 К)f(a)=f(a
К)f(a)=f(a 1)=f(a)f(1)
1)=f(a)f(1)
і
з другого боку, f(a)=f(a)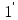 ,
звідси f(a)f(1)=f(a)
,
звідси f(a)f(1)=f(a)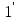 або інакше
або інакше
f(a)[f(1)-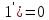
Оскільки
в К
нема дільників нуля і а
можна підібрати так, щоб а
є К
ми включаємо тривіальний випадок: (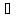 а
а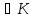 ):
f(a)=0),
то
з наступної рівності виходить, що f(1)=
):
f(a)=0),
то
з наступної рівності виходить, що f(1)=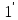 ,
відповідно, і відображення f:
K
,
відповідно, і відображення f:
K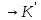
є
таким, що f(1)=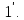 Якщо існує обернений елемент для
Якщо існує обернений елемент для
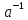 для елементаа
для елементаа К,
то існує обернений елемент для f(a)і
при цьому
К,
то існує обернений елемент для f(a)і
при цьому
f(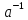 )=
)=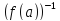 .
.
Твердження випливає із рівностей:
f(a)f(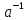 )=f(a
)=f(a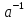 )=f(1)=
)=f(1)=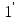 ,
,
f(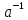 )f(a)=
f(
)f(a)=
f(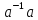 )=f(1)=
)=f(1)=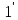 .
.
Для групового гомоморфізму вводять поняття ядрaKerf і області значеньImf. Аналогічні поняття вводяться і для кільцевого гомоморфізму.
Означення
2. Ядром
гомоморфізму f:
K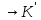 називається
множина Kerfвсіх
тих елементів f
називається
множина Kerfвсіх
тих елементів f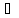 К,
які відображенням f
переводяться в нулевий елемент 0 кільця
К,
які відображенням f
переводяться в нулевий елемент 0 кільця
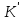 :
:
Ker
f={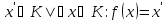 }
}
Областю
знаень або образом гомоморфізму f:
K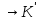 називається
множина Imf
всіх тих елементів в
називається
множина Imf
всіх тих елементів в
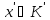 ,
для яких існують такі елементих
,
для яких існують такі елементих
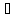 К,
що
К,
що
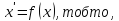
Im
f
={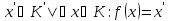 }.
}.
Як
відомо, у випадку групового гомоморфізму
f:
G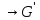 множини
Ker
f
і Im
f
є підгрупами груп G
і
множини
Ker
f
і Im
f
є підгрупами груп G
і
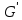 відповідно. Неважко перевірити, що у
випадку кільцевого гомоморфізмуf:
K
відповідно. Неважко перевірити, що у
випадку кільцевого гомоморфізмуf:
K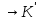 множини
Kerf
і Imf
є підкільцем кільця К
і
множини
Kerf
і Imf
є підкільцем кільця К
і
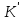 відповідно.
До цього питання ми ще повернемось в
параграфі 3.
відповідно.
До цього питання ми ще повернемось в
параграфі 3.
Приклад.Розглянемо
кільце
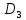 усіх діагональних матриць 3-го порядку.
усіх діагональних матриць 3-го порядку.
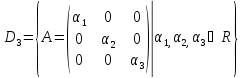
і
кільце
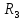 усіх
трьохвимірних векторів
усіх
трьохвимірних векторів
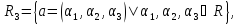
в якому операції задані так:
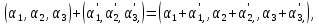
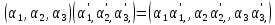
Задамо
відображення f:
D
 таким
способом: якщо
таким
способом: якщо
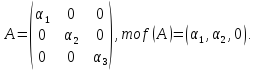
Відображення f є гомоморфізмом:
Якщо
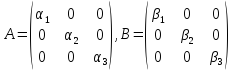 ,то
,то
А+В=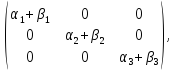 f
(A)=
f
(A)=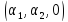 ,f
(B)=(
,f
(B)=(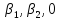 )
)
і значить
f(A+B)=(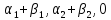 )=(
)=(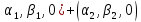 =
f
(A)+
f
(B);
=
f
(A)+
f
(B);
AB=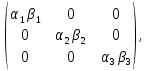
f(AB)=(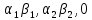 )=(
)=(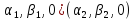 =f
(A)
f
(B);
=f
(A)
f
(B);
Очевидно, що
Kerf=
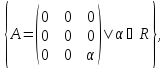
Imf
= {a
= (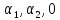 )
|
)
|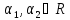 }
}
ІІ.Серед
гомоморфізмів особлива роль належить
ізоморфізмам. Якщо існує ізоморфне
відображення кільця К
на кільце
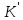 , то кільця К та
, то кільця К та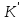 називаютьізоморфними.
Ізоморфні
кільця мають цілком однакові алгебраїчні
властивості і фактично їх можна не
розрізняти. З цієї точки зору цікавим
є наступне твердження.
називаютьізоморфними.
Ізоморфні
кільця мають цілком однакові алгебраїчні
властивості і фактично їх можна не
розрізняти. З цієї точки зору цікавим
є наступне твердження.
Теорема 1. Якщо кільце К ізоморфне множині М з двома алгебраїчними операціями – додавання та множення, то множина М теж є кільцем.
Доведення. Нехай кільце К ізоморфне множині М, на якій означено операції додавання і множення. Нам треба довести, що множина М є кільцем. Оскільки на множині М операції вже означено, то залишається тільки показати, що ці операції задовольняють аксіоми кільця.
Оскільки кільце К ізоморфне М, то відображення ізоморфне f: K→M. Відображення fзокрема є сур’єктивним і , значить:
(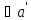 ,
,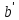 ,
,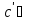 М) (
М) (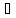 a,
b, c
a,
b, c
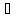 К) :
К) :
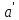 =f(a),
=f(a),
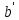 =f(b),
=f(b),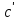 =f(c)
=f(c)
Тоді, в силу гомоморфності відображення f і справедливості аксіом кільця для операцій, означених на К, ми матимемо:
(а′+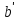 )+
)+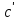 =(
=(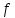 (а)+
(а)+
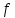 (b))
+ f(c) = f (a+b) + f (c) = f ((a+b)+c);
(b))
+ f(c) = f (a+b) + f (c) = f ((a+b)+c);
f
(a+(b+c))=f (a)+f (b+c)=f (a)+(f (b)+ f (c))=а′+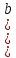 +
+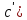 ;
;
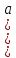 )
)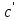 =(
f (a) f (b)) f (c)=f (ab) f (c)=f ((ab)c)=f (a(bc))=f (a) f (bc)=f
(a)( f (b) f (c))=
=(
f (a) f (b)) f (c)=f (ab) f (c)=f ((ab)c)=f (a(bc))=f (a) f (bc)=f
(a)( f (b) f (c))=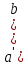 );
);
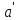 +
+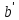 =
f (a)+f (b)=f (a+b)=f (b)+f (a)=
=
f (a)+f (b)=f (a+b)=f (b)+f (a)=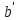 +а′;
+а′;
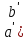 +
+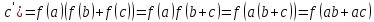 =f
(ab)+f (ac)=f (a) f (b)+f (a) f (c)=а′b′+а′с′.
=f
(ab)+f (ac)=f (a) f (b)+f (a) f (c)=а′b′+а′с′.
Таким чином, операції, означені на множині М, задовольняють аксіоми 1),2), 5), і 6) означення кільця. Роль нулевого елемента в М виконує f(0):
а′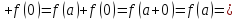 а′,
а′,
протилежним
елементом до елемента
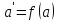 є елементf(-a)
:
є елементf(-a)
:
а′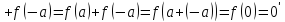 .
.
Отже, множина М є кільцем.
Як бачимо, ізоморфізм переносить алгебраїчні властивості з однієї множини на другу. При допомозі ізоморфізму можна розв’язати і питання про існування обернених елементів. Цим займемося в наступному пункті.
ІІІ.
Поле дробів області цілісності. Якщо
кільце К
є кільцем з одиницею, то деякі елементи
цього кільця мають обернені до себе.
Постараємося з’ясувати, для яких
елементів кільця існують обернені
елементи.Справді, якщо а
— дільник нуля кільця К,
тобто, існує такий елемент
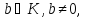 щоab
= 0, то припустивши існування елемента
щоab
= 0, то припустивши існування елемента
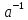 і домноживши останню рівність на
і домноживши останню рівність на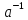 ,
дістанемо:
,
дістанемо:
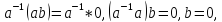 всупереч
умові
всупереч
умові
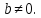
Отже, шукати елементи, що мають обернені, треба серед недільників нуля. Виникає питання: чи кожен елемент, що не є дільником нуля, має обернений? Відповідь одержується, коли з цього погляду розглянути кільце Z цілих чисел. В кільці Zобернені елементи мають тільки 1 і -1. Інші числа обернених елементів не мають і в той же час вони не є дільниками нуля. Отже, не всі недільники нуля мають обернені елементи . Одначе, для кільця Z цілих чисел існує більш широке кільце — поле раціональних чисел, яке містить кільце Z і в якому кожне ненулеве ціле число має обернене число. Тоді можна поставити питання: чи не має місця аналогічна ситуація у випадку довільного кільця К? Виявляється, що має і це можна обґрунтувати ввівши поняття ізоморфного вкладення кільця в кільце.
Означення. Говорять, що кільце К ізоморфно вкладається в кільце K′, якщо існує ізоморфне відображення кільця К на деяке підкільце K′ .
Виявляється,
що кожне кільце К
можна ізоморфно вкласти в кільце K′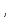 в якому всякий ненулевий елемент, що не
є дільником нуля, має обернений.
Обгрунтуємо зараз це твердження тільки
для того випадку, колиК
— область цілісності. КільцеK′
виявиться при цьому полем. Отже, доведемо
таку теорему.
в якому всякий ненулевий елемент, що не
є дільником нуля, має обернений.
Обгрунтуємо зараз це твердження тільки
для того випадку, колиК
— область цілісності. КільцеK′
виявиться при цьому полем. Отже, доведемо
таку теорему.
Теорема
2.
Всяка область цілісності К
ізоморфно вкладається в поле
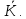
Доведення.
Щоб виробити підхід до доведення даної
теореми, зауважимо, що поле раціональних
чисел, яке містить в собі кільце цілих
чисел і в якому кожне ненулеве ціле
число має обернене, одержується із
кільця Z
шляхом введення дробів
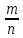 ,
деm,
n
— цілі числа, тобто шляхом розгляду
впорядкованих пар цілих чисел. Доведення
теореми 2 зводиться до фактичної побудови
поля
,
деm,
n
— цілі числа, тобто шляхом розгляду
впорядкованих пар цілих чисел. Доведення
теореми 2 зводиться до фактичної побудови
поля
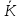 .
Цю побудову здійснюватимемо аналогічно,
як і при побудові поля раціональних
чисел, тобто шляхом розгляду множини
всіх впорядкованих пар елементів з
кільцяК.
.
Цю побудову здійснюватимемо аналогічно,
як і при побудові поля раціональних
чисел, тобто шляхом розгляду множини
всіх впорядкованих пар елементів з
кільцяК.
Отже, розглянемо множину
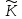 всіх впорядкованих пар (
всіх впорядкованих пар (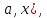
(a,х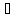 K,
x
K,
x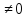 )
елементів із кільця К. Ці пари зручно
записувати у вигляді
)
елементів із кільця К. Ці пари зручно
записувати у вигляді
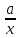 і називати дробами. Введемо в цій множині
відношення рівності таким способом:
дроби
і називати дробами. Введемо в цій множині
відношення рівності таким способом:
дроби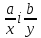 будемо
називати рівними,
будемо
називати рівними,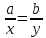 , якщоaу=bх.
Так введемо відношення, яке є відношенням
еквівалентності на множині
, якщоaу=bх.
Так введемо відношення, яке є відношенням
еквівалентності на множині
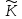 .
Справді, відношення рівності задовольняє
всім трьом умовам з означення відношення
еквівалентності:
.
Справді, відношення рівності задовольняє
всім трьом умовам з означення відношення
еквівалентності:
а)
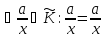 ,
бо aх=
ах
/ рефлективність
̸;
,
бо aх=
ах
/ рефлективність
̸;
б)
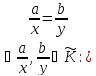 )
)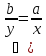 ) , бо з рівності
) , бо з рівності
ау
= bх
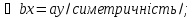
в)
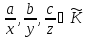 :(
:(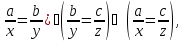 бо перемноживши рівностіау=bх
і bz
= су
(1). Одержимо (ау)(bz)=(bх)(су)
, звідси скориставшись асоціативністю
і комутативністю множення в кільці К
та властивістю
бо перемноживши рівностіау=bх
і bz
= су
(1). Одержимо (ау)(bz)=(bх)(су)
, звідси скориставшись асоціативністю
і комутативністю множення в кільці К
та властивістю
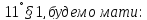 аz
= cx
(2).
аz
= cx
(2).
(це
при умові, що b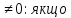 b=с,
то в силу того, що в К
немає дільників нуля, з рівності (1)
випливатиме: а=0,с=0
і тоді рівність (2) очевидна).
b=с,
то в силу того, що в К
немає дільників нуля, з рівності (1)
випливатиме: а=0,с=0
і тоді рівність (2) очевидна).
Відомо,
що всяке відношення еквівалентності
на множині визначає розбиття цієї
множини на класи. Тому введене нами
відношення рівності дробів в множині
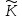 визначає
розбиття цієї множини класи рівних між
собою дробів. Кожен такий клас є сукупністю
всіх рівних між собою дробів і тому він
повністю означається будь-яким своїм
елементом
визначає
розбиття цієї множини класи рівних між
собою дробів. Кожен такий клас є сукупністю
всіх рівних між собою дробів і тому він
повністю означається будь-яким своїм
елементом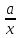 , через це будемо його позначати так:
{
, через це будемо його позначати так:
{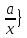 .
Різні такі класи не містять рівних між
собою дробів і об’єднання всіх таких
класів співпадає із множиною
.
Різні такі класи не містять рівних між
собою дробів і об’єднання всіх таких
класів співпадає із множиною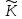 .
Отже,
.
Отже,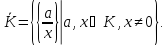
Доведемо, що множина
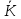 утворює поле. Для цього треба ввести в
множині
утворює поле. Для цього треба ввести в
множині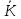 операції
додавання і множення. Введемо їх так:
операції
додавання і множення. Введемо їх так:
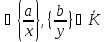 :{
:{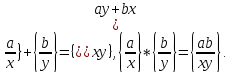
Ці
означення коректні, бо кільце К
є областю цілісності і тому із нерівностей
xy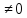 випливає, що x
випливає, що x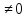 . Покажемо, що так введені операції є
однозначними, тобто, що сума і добуток
класів
. Покажемо, що так введені операції є
однозначними, тобто, що сума і добуток
класів
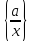 і
і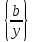 не
залежить від вибору представників
класів. Інакше кажучи, що коли
не
залежить від вибору представників
класів. Інакше кажучи, що коли
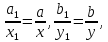 (3)
(3)
то 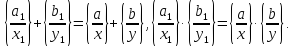 (4)
(4)
Рівність (3) означає, що
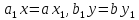 (5)
(5)
Щоб довести рівності (4), треба довести рівності:
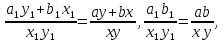
а для цього треба показати справедливість рівностей:
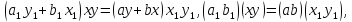
які в силу дистрибутивності і асоціативності рівносильні рівностям:
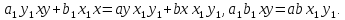
Якщо
врахувати, що в кільці К множення
комутативне, асоціативне і дистрибутивне,
то перша з останніх рівностей одержується
із вірних рівностей (5) домноженням
першої з них на
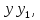 другої
— на
другої
— на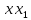 і
наступним додаванням одержаних рівностей,
а друга — почленним перемноження
рівностей (5). Цим справедливість рівностей
(4) доведена.
і
наступним додаванням одержаних рівностей,
а друга — почленним перемноження
рівностей (5). Цим справедливість рівностей
(4) доведена.
Таким
чином, які б не брати дроби із класів
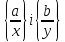 сума
і добуток цих класів залишаються
незмінними.
сума
і добуток цих класів залишаються
незмінними.
Приступимо
до перевірки виконання аксіом поля в
множині
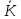 .
Справедливість асоціативності,
комутативності, додавання і множення
та дистрибутивність множення відносно
додавання в множині
.
Справедливість асоціативності,
комутативності, додавання і множення
та дистрибутивність множення відносно
додавання в множині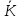 безпосередньо випливає із справедливості
цих властивостей в кільціК.
Перевіримо, наприклад, дистрибутивність
множення відносно додавання:
безпосередньо випливає із справедливості
цих властивостей в кільціК.
Перевіримо, наприклад, дистрибутивність
множення відносно додавання:
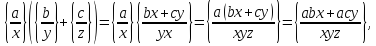
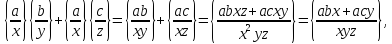
звідки внаслідок рівності правих частин одержуємо:
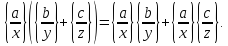
Щоб
вказати нульовий елемент в множині
 , зауважимо, що множина всіх дробів виду
, зауважимо, що множина всіх дробів виду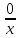 утворює клас рівних дробів, бо
утворює клас рівних дробів, бо
 x,
y
x,
y K; x,
y
K; x,
y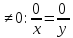
і
з рівності
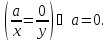
Крім
того,
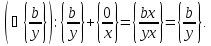
Отже,
нулевим елементом в множині
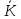 є
клас{
є
клас{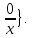 Протилежним
елементом класу
Протилежним
елементом класу
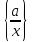 є
клас
є
клас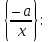
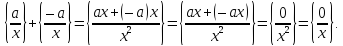
Роль
одиниці в множині К відіграє клас
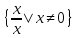 ,
який
складається із усіх дробів з однаковими
ненулевими чисельниками і знаменниками.
Справді,
,
який
складається із усіх дробів з однаковими
ненулевими чисельниками і знаменниками.
Справді,
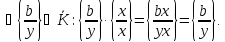
Залишається
тільки помітити, що множина
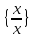 всіх
дробів з рівними чисельниками і
знаменниками справді утворює клас
рівних дробів. Цей факт є наслідком
того, що завжди
всіх
дробів з рівними чисельниками і
знаменниками справді утворює клас
рівних дробів. Цей факт є наслідком
того, що завжди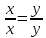 і завжди з рівності
і завжди з рівності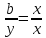 випливаєbx
= xy,
тобто, b
= y.
Якщо клас
випливаєbx
= xy,
тобто, b
= y.
Якщо клас
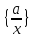 є ненулевим, тобто,a
є ненулевим, тобто,a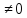 ,
то оберненим до цього класу є клас
,
то оберненим до цього класу є клас
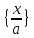 ,
що містить дріб
,
що містить дріб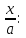
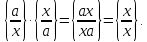
Таким
чином, множина
 задовольняє всім аксіомам з означення
поля
задовольняє всім аксіомам з означення
поля і тому вона є полем.
і тому вона є полем.
III.
Покажемо нарешті, що кільце К ізоморфне
підмножині поля
 в силу теореми 1 ця підмножина буде
підкільцем. Вибір цієї підмножини
показує нам ситуацію у випадку кільцяZ
цілих чисел ціле число а
завжди
дорівнює дробові
в силу теореми 1 ця підмножина буде
підкільцем. Вибір цієї підмножини
показує нам ситуацію у випадку кільцяZ
цілих чисел ціле число а
завжди
дорівнює дробові
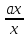 ,
дех
— довільне ненулеве ціле число. Якщо у
випадку довільного кільця виявиться,
що множини дробів
,
дех
— довільне ненулеве ціле число. Якщо у
випадку довільного кільця виявиться,
що множини дробів
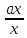 ,
деа
—
фіксований елемент кільця К
і х
пробігає всю множину К\{0}
є класами рівних дробів, то можна
сподіватися, що поставивши у відповідність
елементу
,
деа
—
фіксований елемент кільця К
і х
пробігає всю множину К\{0}
є класами рівних дробів, то можна
сподіватися, що поставивши у відповідність
елементу
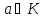 клас
клас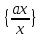 ,
одержимо ізоморфне відображення кільцяК
на множину таких дробів.
,
одержимо ізоморфне відображення кільцяК
на множину таких дробів.
Множина
всіх дробів виду
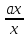 ,
де
а
—
фіксований елемент кільця К
і х
пробігає
К\{0}
утворює
клас рівних дробів, бо
,
де
а
—
фіксований елемент кільця К
і х
пробігає
К\{0}
утворює
клас рівних дробів, бо
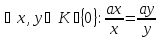
і
з рівності
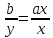 виходить,
щоbx
= axy,
тобто
b
= ay.
виходить,
щоbx
= axy,
тобто
b
= ay.
Задамо
відображення f
: K таким способом:
таким способом:
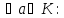 f(a)
= {
f(a)
= {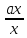 }.
}.
Відображення fє бієктивним відображенням кільця Кна підмножину
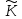 o
= {{
o
= {{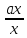 }|a
}|a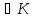 }:
}:
бо
якби
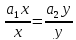 ,
то
,
то
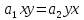 , звідсивнаслідок
того, що в К
немає дільників нуля, на підставі
властивості
, звідсивнаслідок
того, що в К
немає дільників нуля, на підставі
властивості
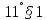 випливатиме
випливатиме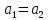 ,
всупереч
умові.
,
всупереч
умові.
б) відповідно до означення відображення f
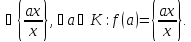
Відображення f гомоморфне:
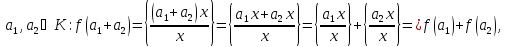
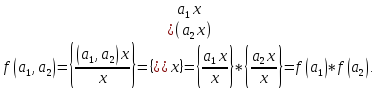
Отже,
відображення fє
ізоморфним відображенням кільця К
на підкільце
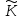 o
кільця
o
кільця
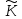 (множина
(множина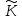 o
є підкільцем кільця
o
є підкільцем кільця
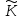 на підставі теореми 1 і того очевидного
факту, що сума і добуток елементів із
на підставі теореми 1 і того очевидного
факту, що сума і добуток елементів із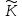 o
знову належать
o
знову належать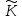 o).
Цим доведено, що область цілісності К
ізоморфно вкладається в поле
o).
Цим доведено, що область цілісності К
ізоморфно вкладається в поле
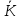 .
.
В
алгебрі побудована при доведенні теореми
2 поле
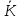 називають полем дробів або полем часток
області цілісностіК.
називають полем дробів або полем часток
області цілісностіК.