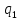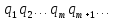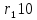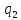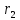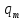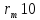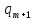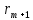- •§1. Алгебраїчні структури з однією операцією. Означення групи, найпростіші властивості груп.
- •IV. Деякі інші означення групи
- •2. Підгрупи. Циклічні групи.
- •§1. Означення кільця, властивості та основні поняття. Приклади кілець.
- •2.Гомоморфізми та ізоморфізми кілець
- •§ 3. Ідеали кілець.
- •1.Означення ідеалу кільця, приклади ідеалів.
- •2. Кільця головних ідеалів та евклідові кільця.
- •§5. Конгруенції та фактор кільця за ідеалом.
- •2.Фактор-кільця комутативного кільця за ідеалом і.
- •3. Фактор-кільця і гомоморфізми.
- •4. Конгруенції за модулем
- •§6. Класи лишків кільця цілих чисел за модулем .
- •1.Конгруенції та класи лишків за модулем
- •2. Кільце класів лишків за модулем .
- •§7 Деякі арифметичні застосування теорії конгруенцій
- •1. Застосування конгруенцій до встановлення ознак подільності.
- •2. Перетворення звичайного дробу в систематичний і визначення довжини періоду систематичного дробу.
2. Перетворення звичайного дробу в систематичний і визначення довжини періоду систематичного дробу.
Розглянемо
питання про перетворення звичайного
дробу в десятковий. Як відомо з арифметики
звичайні дроби перетворюються або в
скінченні, або не в скінченні періодичні
десяткові дроби. При цьому звичайний
дріб
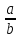 перетворюється в скінченний десятковий
дріб тоді і тільки тоді, коли канонічний
розклад знаменника має вигляд
перетворюється в скінченний десятковий
дріб тоді і тільки тоді, коли канонічний
розклад знаменника має вигляд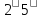 .
тобто не містить ніяких простих множників,
крім 2 і 5. Для спрощення вважатимемо
.
тобто не містить ніяких простих множників,
крім 2 і 5. Для спрощення вважатимемо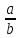 нескоротним правильним дробом.(Якщо
він неправильний, то можна спочатку
виділити цілу частину). Звичайні
нескоротні і правильні дроби виду
нескоротним правильним дробом.(Якщо
він неправильний, то можна спочатку
виділити цілу частину). Звичайні
нескоротні і правильні дроби виду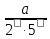 перетворюються в скінченні десяткові
дроби з числом десяткових знаків, яке
дорівнює найбільшому з чисел
або .
Справді, якщо =
то
перетворюються в скінченні десяткові
дроби з числом десяткових знаків, яке
дорівнює найбільшому з чисел
або .
Справді, якщо =
то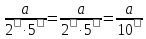 скінченний десятковий дріб. Якщо
скінченний десятковий дріб. Якщо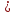 ,
то
,
то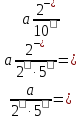 скінченний десятковий дріб. Якщо
скінченний десятковий дріб. Якщо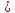 ,
то
,
то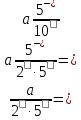 скінченний десятковий дріб.
скінченний десятковий дріб.
Легко
зрозуміти, що нескоротний дріб виду
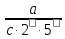 ,
де
,
де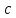 відмінне від 2 і 5, в скінченний десятковий
дріб не перетворюється.
відмінне від 2 і 5, в скінченний десятковий
дріб не перетворюється.
Справді, припускаючи супротивне,маємо
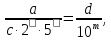
Звідки
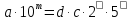 ,
де
,
де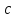 – дільник числа
– дільник числа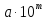 ,
що неможливо, бо
,
що неможливо, бо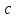 відмінне від 2 і 5 за умовою і
відмінне від 2 і 5 за умовою і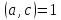 .
Ця суперечність доводить справедливість
твердження.
.
Ця суперечність доводить справедливість
твердження.
Теорема
1.
Якщо канонічний розклад знаменника
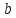 нескороченого дробу
нескороченого дробу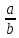 не містить у собі множників 2 і 5, то цей
дріб перетворюється у чистий періодичний
десятковий дріб; при цьому число цифр
у періоді дорівнює показнику,
до якого належить число 10, за модулем
не містить у собі множників 2 і 5, то цей
дріб перетворюється у чистий періодичний
десятковий дріб; при цьому число цифр
у періоді дорівнює показнику,
до якого належить число 10, за модулем
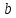 .
.
Доведення.
Для спрощення дріб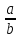 вважатимемо правильним. Процес ділення
числа
вважатимемо правильним. Процес ділення
числа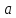 на
число
на
число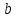 при умові
при умові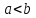 можна схематично зобразити так:
можна схематично зобразити так:
|
_ a10 b
|
B | ||
|
0, | |||
|
_
b
| |||
|
……. | |||
|
|
|
_
b
| |
|
|
|
|
_
b
|
|
|
|
|
……… |
Цю схему в свою чергу можна подати у вигляді системи рівностей:

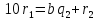
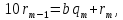

Де
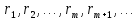 —
остачі, а
—
остачі, а
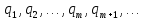 —
частки проміжних обчислень. Будь-яка
остача
—
частки проміжних обчислень. Будь-яка
остача
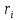 ,
очевидно, задовольняє нерівність
,
очевидно, задовольняє нерівність
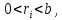
а
будь-які числа
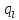 задовольняють нерівність
задовольняють нерівність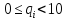 ,
тобто є цифрами, з яких складається
частка 0,
,
тобто є цифрами, з яких складається
частка 0,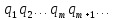 в схемі (4).
в схемі (4).
Проаналізуємо
властивості чисел
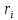 і
і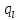 докладніше. Насамперед нагадаємо, що
дріб
докладніше. Насамперед нагадаємо, що
дріб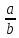 є нескоротним і правильним. Це означає,
що
є нескоротним і правильним. Це означає,
що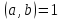 і
і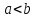 .
Таким чином, число
.
Таким чином, число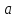 є один з найменших додатних лишків ЗСЛ
за модулем
є один з найменших додатних лишків ЗСЛ
за модулем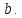 Справді
Справді
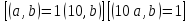
Оскільки
числа
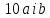 взаємно прості, то з першої рівності
(5) випливає, що
взаємно прості, то з першої рівності
(5) випливає, що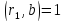 .
Справді за умови
.
Справді за умови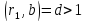 випливало б, що вся права частина, а
отже, і ліва частина ділилась би на
випливало б, що вся права частина, а
отже, і ліва частина ділилась би на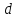 . Тому числа
. Тому числа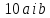 не були б взаємно простими, що суперечить
(7). За умов
не були б взаємно простими, що суперечить
(7). За умов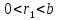 і
і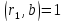 випливає,
що остача
випливає,
що остача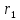 є одним з найменших додатних лишків
ЗСЛ за модулем
є одним з найменших додатних лишків
ЗСЛ за модулем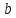 . Аналогічно можна показати, що й числа
. Аналогічно можна показати, що й числа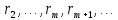 є найменшими додатними лишками ЗСЛ за
модулем
є найменшими додатними лишками ЗСЛ за
модулем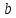 .
Але ЗСЛ за модулем
.
Але ЗСЛ за модулем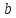 може мати не більше
може мати не більше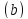 найменших додатних лишків. Тому в системі
рівностей (5) настане момент, коли одна
з остач дорівнюватиме
найменших додатних лишків. Тому в системі
рівностей (5) настане момент, коли одна
з остач дорівнюватиме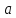 .
Нехай
.
Нехай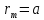 .
Тоді
.
Тоді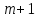 рівність (5) збіжиться з першою рівністю
цієї системи. І тому … . Далі, … рівність
збіжиться з другою рівністю (5) і тому
рівність (5) збіжиться з першою рівністю
цієї системи. І тому … . Далі, … рівність
збіжиться з другою рівністю (5) і тому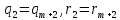 .
Таким чином, остачі
.
Таким чином, остачі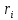 і частки
і частки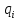 проміжних обчислень повторюватимуться.
Тим самим частка в схемі (4) буде чистим
періодичним десятковим дробом виду
проміжних обчислень повторюватимуться.
Тим самим частка в схемі (4) буде чистим
періодичним десятковим дробом виду
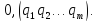
Для
доведення теореми залишається показати,
що перше повторення настане після
кроків проміжних обчислень, де
– показник, до якого належить 10 за
модулем
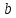 . Справді, якщо
– найменший показник, при якому
здійснюється конгруенція
. Справді, якщо
– найменший показник, при якому
здійснюється конгруенція
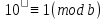
то
при
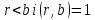 рівносильною їй є і конгруенція
рівносильною їй є і конгруенція
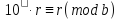
Остання
конгруенція якраз і показує, що, приписавши
до
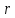 нулів, що відповідає визначенню
послідовних цифр частки, дістанемо при
діленні
нулів, що відповідає визначенню
послідовних цифр частки, дістанемо при
діленні
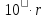 на
на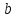 остачу
остачу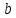 .
При діленні
.
При діленні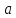 на
на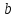 при
при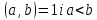 аналогічно дістанемо через
ділень остачу, яка дорівнює числу
аналогічно дістанемо через
ділень остачу, яка дорівнює числу
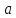 .
Отже, частка (8) має вигляд
.
Отже, частка (8) має вигляд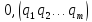 ,
що й треба було довести.
,
що й треба було довести.
Зауваження.
З конгруенції
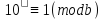 випливає, що
випливає, що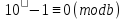 або
або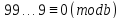 .
.
Іншими
словами, число 999…9, що складається з
дев’яток
– найменше з можливих чисел такої
структури, яке ділиться на
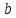 .
Це дає можливість досить легко знаходити
число.
Для цього треба послідовно ділити на
.
Це дає можливість досить легко знаходити
число.
Для цього треба послідовно ділити на
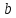 числа 9, 99, 999, 9999, … і т. д., аж поки таке
ділення не відбудеться. Кількість
дев’яток у такому числі і дорівнює
числу.
числа 9, 99, 999, 9999, … і т. д., аж поки таке
ділення не відбудеться. Кількість
дев’яток у такому числі і дорівнює
числу.
Теорема
2.
Якщо канонічний розклад знаменника
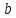 нескоротного дробу
нескоротного дробу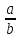 має вигляд
має вигляд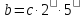 ,де
,де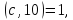 то цей дріб перетворюється у мішаний
періодичний дріб; число цифр до періоду
дорівнює,
де
– найбільше з чисел
і
; число цифр періоду дорівнює ,
де
– показник, якому належить число 10 за
модулем
то цей дріб перетворюється у мішаний
періодичний дріб; число цифр до періоду
дорівнює,
де
– найбільше з чисел
і
; число цифр періоду дорівнює ,
де
– показник, якому належить число 10 за
модулем
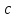 .
.
Доведення. Дріб
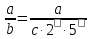
помножимо
на
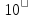 , де
, де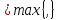 . Матимемо
. Матимемо
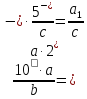
і далі
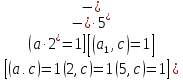
За
теоремою 1, дріб
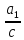 перетворюється в чистий періодичний
дріб з числом цифр у періоді, яке дорівнює,
де
– показник, до якого належить 10 за
модулем
перетворюється в чистий періодичний
дріб з числом цифр у періоді, яке дорівнює,
де
– показник, до якого належить 10 за
модулем
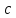 .
Щоб з нього дістати початковий дріб
.
Щоб з нього дістати початковий дріб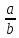 ,
треба розділити його на
,
треба розділити його на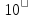 ,
або інакше, перенести кому в знайденому
періодичному дробі на
знаків ліворуч; у результаті дістанемо
мішаний періодичний дріб з числом
цифр до періоду. Теорему доведено.
,
або інакше, перенести кому в знайденому
періодичному дробі на
знаків ліворуч; у результаті дістанемо
мішаний періодичний дріб з числом
цифр до періоду. Теорему доведено.
Приклади.
1.
Знайти число цифр періоду десяткового
періодичного дробу, в який перетворюється
дріб
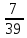 .
.
Ділимо
на 39 послідовно числа 9, 99, 999, 9999, 99999.
Нарешті з’ясовується, що тільки число
999999 націло ділиться на 39. Кількість
дев’яток у цьому числі визначає довжину
періоду:
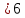 .
.
2.
Знайти число цифр, яке міститься до
періоду, і довжину періоду періодичного
дробу, в який перетворюється дріб
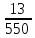 .
.
Знаменник
цього дробу в канонічному розкладі має
вигляд
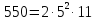 .
Тому
.
Тому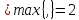 є найбільшим з показників степеня цифр
2 і 5. Це означає, що періодичний десятковий
дріб має дві цифри до періоду. Найменше
з чисел, складених з дев’яток,
яке ділиться
на 11, є
число
99. Воно складається з двох дев’яток. Це
означає, що довжина … періоду періодичного
дробу дорівнює 2. І справді, як неважко
перевірити, розглядуваний дріб
перетворюється в такий періодичний
дріб:
є найбільшим з показників степеня цифр
2 і 5. Це означає, що періодичний десятковий
дріб має дві цифри до періоду. Найменше
з чисел, складених з дев’яток,
яке ділиться
на 11, є
число
99. Воно складається з двох дев’яток. Це
означає, що довжина … періоду періодичного
дробу дорівнює 2. І справді, як неважко
перевірити, розглядуваний дріб
перетворюється в такий періодичний
дріб:
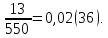
.