1. Застосування конгруенцій до встановлення ознак подільності.

Як відомо, в кільці Z цілих чисел визначені операції додавання, віднімання і множення, а дія ділення не завжди можлива. Тому виникає потреба визначити, при яких умовах цілі числа діляться одно на одне.

Подільність чисел – це певне відношення між числами, яке в Z₊ має такі властивості: рефлективність (aa) , транзитивність () і антисиметричність. Будь-яке відношення, яке має властивості рефлективності, транзитивності і анти симетричності. Називається відношенням не строгого порядку. Отже, подільність чисел в Z₊ є відношенням не строгого порядку. Аналогічним відношенням частинної упорядкованості є, наприклад, відношення «» в кільціZ. Воно рефлексивне , транзитивне [a b b c][ab]), антисиметричне .

Між відношеннями подільності і в кільціZ можна встановити і таку аналогію. Відношення a ⋮b означає, що існує таке число с, при якому виконується рівність a = bc. Відношення , або, означає, що існує таке число, при якому. Рівностіі, як бачимо, аналогічні.

Факт подільності двох чисел можна, звичайно, встановити за допомогою алгоритму ділення чисел з остачею. Проте для великих чисел це завдання досить складне. Тому бажано знайти зручні ознаки, за якими можна було б судити про подільність чисел, не виконуючи самого ділення. В цілому суть ознак подільності зводиться до того, що розгляд подільності деякого натурального числа a на натуральне число m змінюється розглядом подільності на число m іншого, меншого за a натурального числа b, яке можна знайти за деяким правилом, що визначається числовою функцією , тобто. При цьому числає, як кажуть. Рівноподільними на число, тобто такі, які одночасно діляться або одночасно не діляться на число. Часто вимагають, щоб вони були конгруентними за модулем.

Одним із способів знаходження ознак подільності, основаних на конгруентності чисел, є так званий спосіб Паскаля¹. Нехай деяке натуральне число при основі численнямає вигляд

,

де коефіцієнти є натуральні числа, які задовольняють нерівності. Позначимо черезостачу від ділення числана ,тобто 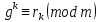,і побудуємо число за таким правилом:

На основі властивості 9 п. 15.1 . Оскільки, то дістаємо таку ознаку Паскаля подільності чисел:

Якщо число ділиться на числоm, то ділиться на нього і число .

Якщо ж b на число m не ділиться, то не ділиться на m і число a.

За допомогою цієї загальної ознаки можна встановити зручні конкретні ознаки подільності чисел, записаних у звичайній для нас десятковій системі числення. У цій системі і числомає вигляд:

Коротко це можна записати так: .

а) Ознака подільності на 2 і на 5.

Оскільки , то всі остачівід діленняна числа 2 і 5 дорівнюють нулю. Тому за формулою (2) число. Отже, маємо таку ознаку:

Число a ділиться на 2 і на 5 тоді і тільки тоді, коли на них ділиться цифра одиниць числа a.

Приклад 1. Число . Число 8127 не ділиться на 5, бо 7 не ділиться на 5.

б) Ознака подільності на 3 і на 9.

Оскільки всі остачі від діленняна число 3 або 9 дорівнюють 1, то за (2)

Отже, маємо таку ознаку:

Число a ділиться на 3 (або на 9) тоді і тільки тоді, коли сума цифр, які його зображують, ділиться на 3 (або відповідно на 9).

Приклад 2. Число .

в) Ознака подільності на 11.

За модулем 11 маємо

Тому , і, отже, за рівністю (2)

Враховуючи, що цифри з парними індексами в числістоять на непарних місцях, можна сформулювати таку ознаку:

Число a ділиться на 11 тоді і тільки тоді, коли різниця між сумою цифр, які стоять на непарних місцях, і сумою цифр. Які стоять на парних місцях, ділиться на 11.

Приклад 3. Число , бо число

ділиться на 11.

У системі числення з основою можна знайти зручні ознаки подільності на числа 4, 25, 50. Числов цій системі можна записати так:

Порівнюючи це з (3), бачимо, що, тобто є двоцифровим числом, яке зображується двома останніми цифрами числав десятковій системі числення.

Враховуючи, що і числаділяться на числа 4, 25, 50, дістаємо такі ознаки подільності:

Число ділиться на 4 (або відповідно 25 чи 50) ділиться двоцифрове число, утворене двома останніми цифрами числа, записаного в десятковій системі числення.

Ознаки подільності є цінними, якщо вони прості, зручні для користування. Проте більшість ознак, які можна вивести з ознаки Паскаля, є складними. Існує ряд зручних ознак подільності, які не випливають з загальної ознаки Паскаля, а знайдені іншими способами. Наприклад, одну з ознак подільності на 7 можна сформулювати так:

Число ділиться на7 тоді і тільки тобі, коли ділиться на 7 число .

Зазначимо, що на відміну від усіх попередніх ознак числа тут рівноподільні на7, а не конгруентні між собою за модулем.

Приклад 4. .

Оскільки не ділиться на 7, то не ділиться на 7 і число 285. Зазначимо, що при діленні на 7 числа 285 дістаємо остачу 5, а при діленні на 7 числа 18 остача дорівнює 4 і тому.

Приклад 5. Встановити, чи ділиться на 7 число .

Приклад можна розв’язати так. Перш за все і тому. А. Тому. Оскількито й число.