
- •§1. Алгебраїчні структури з однією операцією. Означення групи, найпростіші властивості груп.
- •IV. Деякі інші означення групи
- •2. Підгрупи. Циклічні групи.
- •§1. Означення кільця, властивості та основні поняття. Приклади кілець.
- •2.Гомоморфізми та ізоморфізми кілець
- •§ 3. Ідеали кілець.
- •1.Означення ідеалу кільця, приклади ідеалів.
- •2. Кільця головних ідеалів та евклідові кільця.
- •§5. Конгруенції та фактор кільця за ідеалом.
- •2.Фактор-кільця комутативного кільця за ідеалом і.
- •3. Фактор-кільця і гомоморфізми.
- •4. Конгруенції за модулем
- •§6. Класи лишків кільця цілих чисел за модулем .
- •1.Конгруенції та класи лишків за модулем
- •2. Кільце класів лишків за модулем .
- •§7 Деякі арифметичні застосування теорії конгруенцій
- •1. Застосування конгруенцій до встановлення ознак подільності.
- •2. Перетворення звичайного дробу в систематичний і визначення довжини періоду систематичного дробу.
2. Кільце класів лишків за модулем .
Вище
вже відзначалося, що сукупність усіх
класів лишків
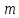 утворює
кільце відносно операцій додавання і
множення суміжних класів – фактор-кільце
утворює
кільце відносно операцій додавання і
множення суміжних класів – фактор-кільце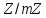 .
Дослідимо, чи не є це кільце полем.
.
Дослідимо, чи не є це кільце полем.
Лема.
Сукупність
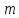 класів лишків
класів лишків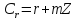 ,
взаємно простих з модулем
,
взаємно простих з модулем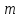 ,
утворив у фактор-кільці
,
утворив у фактор-кільці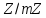 абелеву мультиплікативну групу порядку
абелеву мультиплікативну групу порядку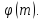
Доведення.
Відзначимо насамперед, що коли ,
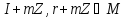 ,
то
,
то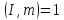 і
і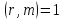 ,
внаслідок чого
,
внаслідок чого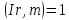 .
З цього виходить, що добуток довільних
суміжних класів із
.
З цього виходить, що добуток довільних
суміжних класів із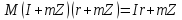 належить
належить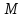 ,
фсоціативність і комутативніеть множення
класів справедлива, бо
,
фсоціативність і комутативніеть множення
класів справедлива, бо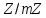 є комутативним кільцем. Внаслідок
співвідношення
є комутативним кільцем. Внаслідок
співвідношення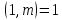
одиничний
клас
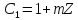 фактор-кільця
фактор-кільця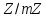 належить
належить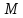 . Для завершення доведення залишається
показати, що кожен елемент
. Для завершення доведення залишається
показати, що кожен елемент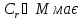 обернений елемент, що теж належить
обернений елемент, що теж належить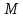 .
.
Нехай
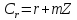 - довільний клас із
- довільний клас із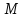 .
Тоді
.
Тоді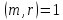 і за теоремою 2 §4
і за теоремою 2 §4
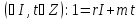
останньої
рівності зокрема виходить що
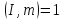 ,
тобто клас
,
тобто клас
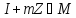 .
Крім того
.
Крім того
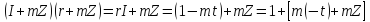
Легко
бачити, що
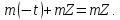 Тому
Тому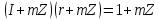 ,
тобто клас
,
тобто клас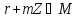 є оберненим до класу
є оберненим до класу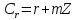 .
.
Таким
чином,
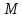 -
мультиплікативпа абелева група. Оскільки
за відзначеним в кінці п.1 класів лишків,
взаємно простих з модулем
-
мультиплікативпа абелева група. Оскільки
за відзначеним в кінці п.1 класів лишків,
взаємно простих з модулем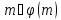 ,
то порядок
,
то порядок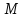 дорівнює
дорівнює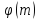 .
Лема доведена.
.
Лема доведена.
Теорема
2.
Якщоp-
просте число, то кільце
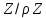 класів лишків за модулем
класів лишків за модулем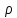 є полем. Якщо
є полем. Якщо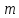 - складене число, то кільце
- складене число, то кільце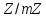 не є навіть областю цілісності.
не є навіть областю цілісності.
Доведення.
Якщо
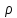 - просте число, то кожне з чисел
1,2,...,
- просте число, то кожне з чисел
1,2,...,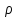 -1
взаємно прості з р. Томувсі класи
-1
взаємно прості з р. Томувсі класи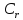 лишківза модулем
лишківза модулем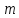 ,
крім нульового класу
,
крім нульового класу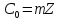 належить абелевій мультиплікативній
групі
належить абелевій мультиплікативній
групі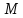 ,
про яку йде мова в лемі. Це і означає,
що в мультиплікативному кільці
,
про яку йде мова в лемі. Це і означає,
що в мультиплікативному кільці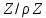 зодиницею
зодиницею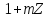 всі
елементи, крім нульового, мають обернені,
тобто
всі
елементи, крім нульового, мають обернені,
тобто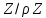 є полем.
є полем.Нехай
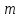 -
складене число. Оскільки
-
складене число. Оскільки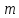 має нетривіальні натуральні дільники,
що, звичайно, менші за нього, то
має нетривіальні натуральні дільники,
що, звичайно, менші за нього, то
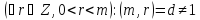
Покажемо,
що клас
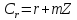 є дільником нуля. Оскільки
є дільником нуля. Оскільки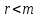 , то
, то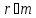 і, значить, клас
і, значить, клас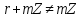 , тобто, не є нулівим класом кільця
, тобто, не є нулівим класом кільця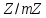 .
Крім того, на підставі /І/.
.
Крім того, на підставі /І/.
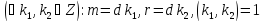
Внаслідок
того, що
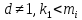 ,
значить,
,
значить,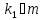 , тобто, клас
, тобто, клас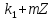 , є ненульовкм. В той же час
, є ненульовкм. В той же час
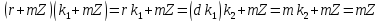
Отже,
в кільці
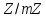 існують дільники нуля, тобто,
існують дільники нуля, тобто,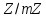 .
не є областю цілісності і, тим більше,
не є полем.
.
не є областю цілісності і, тим більше,
не є полем.
На закінчення цього параграфу використаємо доведену вище лему до доведення важливої теореми теорії чисел - теореми Ейлера.
Теорема 3. (Ейлера)
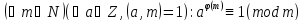
Доведення.
Оскільки
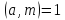 то
клас
то
клас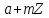 належить сукупності
належить сукупності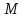 класів лишків, взаємно простих з модулем
класів лишків, взаємно простих з модулем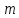 .
За
лемою множина
.
За
лемою множина
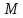 є мультиплікативною абелевою групою
порядку
є мультиплікативною абелевою групою
порядку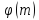 .
Розглянемо в групі
.
Розглянемо в групі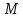 циклічну підгрупу
циклічну підгрупу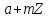 ,
породжену класом
,
породжену класом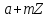 .
На підставі теореми Лагранжа порядок
б цієї підгрупи є дільником порядку
.
На підставі теореми Лагранжа порядок
б цієї підгрупи є дільником порядку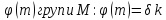 .
.
Тому, що порядок циклічної підгрупи співпадає з порядком породжуючого її елемента,
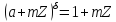 ,
,
внаслідок чого
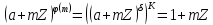
інакше кажучи,
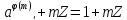
Остання
рівність показує, що
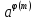 іІ
належать до одного і того ж суміжного
класу за модулем і тому на підставі
іІ
належать до одного і того ж суміжного
класу за модулем і тому на підставі
теореми 2 §5
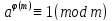
Якщо
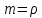 - просте число, то
- просте число, то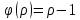 і
теорему Ейлера можна формулювати так:
і
теорему Ейлера можна формулювати так:
ТеоремаФерма.
Якщо
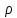 - будь-яке просте число і
- будь-яке просте число і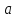 - довільне ціле число, що не ділиться на
- довільне ціле число, що не ділиться на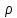 ,то
,то
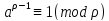
Часто теорему Ферма подають в такій формі:
Якщо
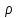 - просте число, то
- просте число, то
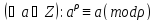
Якщо
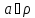 , то справедливість останньої конгруенції
очевидна. Якщо
, то справедливість останньої конгруенції
очевидна. Якщо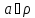 , то остання конгруенція одержується з
попередньої домножуванням на
, то остання конгруенція одержується з
попередньої домножуванням на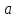 ,
що конгруенції не порушує.
,
що конгруенції не порушує.
