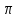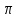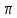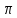- •§1. Алгебраїчні структури з однією операцією. Означення групи, найпростіші властивості груп.
- •IV. Деякі інші означення групи
- •2. Підгрупи. Циклічні групи.
- •§1. Означення кільця, властивості та основні поняття. Приклади кілець.
- •2.Гомоморфізми та ізоморфізми кілець
- •§ 3. Ідеали кілець.
- •1.Означення ідеалу кільця, приклади ідеалів.
- •2. Кільця головних ідеалів та евклідові кільця.
- •§5. Конгруенції та фактор кільця за ідеалом.
- •2.Фактор-кільця комутативного кільця за ідеалом і.
- •3. Фактор-кільця і гомоморфізми.
- •4. Конгруенції за модулем
- •§6. Класи лишків кільця цілих чисел за модулем .
- •1.Конгруенції та класи лишків за модулем
- •2. Кільце класів лишків за модулем .
- •§7 Деякі арифметичні застосування теорії конгруенцій
- •1. Застосування конгруенцій до встановлення ознак подільності.
- •2. Перетворення звичайного дробу в систематичний і визначення довжини періоду систематичного дробу.
ГРУПИ
Література:
А. Г. Курош, курс высшей алгебры, М
Б. Л. Вандер Ванден, Современная алгебра, ч. І, М.-Л, ОГИЗ, 1947г.
Л. А. Калужин, Введение в общую алгебру, М, Наука, 1973г.
Як зазначалось в курсі алгебри першого семестру, основним об’єктом вивчення в алгебрі є алгебраїчні структури. Під алгебраїчною структурою розуміють множину М, на якій задана деяка система алгебраїчних операцій, які задовольняють деякі умови-аксіоми структури. Як відомо, алгебраїчні операції діляться на два типи:внутрішні закони композиції і зовнішні закони композиції. В даному розділі під алгебраїчною операцією, означеною на множині М, розумітимемо скрізь бінарний внутрішній закон композиції на М, тобто відображення прямого добутку М×М в М.
Раніше ми ознайомилися з однією важливою алгебраїчною структурою — полем. Структура поля означається шляхом задання на множині двох алгебраїчних операцій — додавання і множення, які задовольнють відомим дев’яти аксіомам. Але найпростіші серед алгебраїчних структур є структури, які означаються однією алгебраїчною операцією. До вивчення таких структур ми зараз і приступимо.
§1. Алгебраїчні структури з однією операцією. Означення групи, найпростіші властивості груп.
І. АЛГЕБРАЇЧНІ CТРУКТУРИ З ОДНІЄЮ ОПЕРАЦІЄЮ.
Означення 1. Не порожня множина М, на якій означена одна алгебраїчна операція, називається групоїдом.
Алгебраїчну операцію що визначає групоїд, будемо найчастіше називати множенням і вживати мультиплікативний запис a×b. Підкреслимо, що операція, яка визначає групоїд М, повинна бути скрізь означеною на множині М, тобто
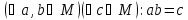
Щоб
відзначити, що групоїд визначається
двома компонентами — множиною М
і алгебраїчною операцією, означеною на
ній, — часом для групоїда вживають таке
позначення:
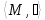 .
Як видно з означення, на операцію, яка
визначає групоїд, не накладається жодних
умов.
.
Як видно з означення, на операцію, яка
визначає групоїд, не накладається жодних
умов.
Приклади.
1. Множина всіх векторів трьохвимірного простору R, є групоїдом, якщо під алгебраїчною розуміти операцію знаходження векторного добутку двох векторів.
2. Множина всіх підстановок n-го степеня з операцією множення підстановок утворює групоїд.
3.
Якщо в множині R
всіх дійсних чисел розглядати тільки
операцію додавання чисел, то сукупність
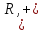 є
групоїдом.
є
групоїдом.
Як відомо, операція знаходження векторного добутку двох векторів є асоціативною і комутативною, відносно неї не існує нейтрального елемента. Операція множення підстановок є асоціативною, але не є комутативною, відносно неї існує одиничний елемент і для кожної підстановки — обернена. Операція додавання дійсних чисел є асоціативною і комутативною, відносно неї існує нульовий елемент і для кожного числа — протилежне.
Як бачимо, в деяких групоїдах алгебраїчна операція насправді задовольняє тим чи іншим умовам. Це дає можливість прокласифікувати групоїд в залежності від того, яким умовам задовольняє алгебраїчна операція групоїду. Ми зупинимось тільки на двох класах групоїдах — півгрупах і групах. Півгрупа — це групоїд, алгебраїчна операція якого є асоціативною. Група — це півгрупа, в якій існує одиничний елемент і для кожного елемента — обернений. Зараз дамо детальніші означення цих об’єктів і вивчимо їх деякі властивості.
ІІ. ПІВГРУПА.
Означення 2. Непорожня множина М, на якій означена одна алгебраїчна операція, яка є асоціативною, називається півгрупою.
Приклади.
Множина всіх підстановок n-го степеня з операцією множення підстановок утворює півгрупу.
Групоїд
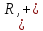 ,
деR
— множина всіх дійсних чисел, теж є
півгрупою.
,
деR
— множина всіх дійсних чисел, теж є
півгрупою.Множина всіх матриць n-го порядку утворює півгрупу відносно операції множення матриць, бо множення матриць є асоціативним. В цій півгрупі існує одиничний елемент — одинична матриця Е, але не для кожної матриці існує обернена.
Сукупність
 і
і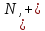 ,
деN—
множина натуральних чисел, утворюють
півгрупи, причому в першому випадку
нейтральний елемент (І)
належить півгрупі, а в другому випадку
півгрупа не містить нейтрального
елемента (0).
,
деN—
множина натуральних чисел, утворюють
півгрупи, причому в першому випадку
нейтральний елемент (І)
належить півгрупі, а в другому випадку
півгрупа не містить нейтрального
елемента (0).Множина P всіх цілих парних чисел утворює півгрупу відносно операції множення (добуток парних чисел — парне число, множення чисел асоціативне), причому ця півгрупа нейтрального елемента (І) не містить.
Наявність
асоціативного закону для операції
півгрупи М
дозволяє однозначно ввести в М
поняття добутку 3, 4, …, nелементів.
Оскільки
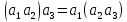 ,
то добуток
,
то добуток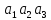 трьох
елементів можна прийняти будь–який із
елементів
трьох
елементів можна прийняти будь–який із
елементів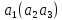 і
і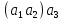 .
Приймемо за означенням:
.
Приймемо за означенням: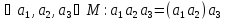
Добуток 4, 5, …, nелементів означимо рекурентно:
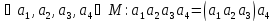
……………………………………………………………………………………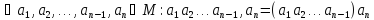
Наявність асоціативного закону для операції півгрупи дозволяє в добутках, що містять більше двох співмножників (такі добутки будемо умовно називати складеними), довільно розставляти дужки. Цей факт випливає з такої теореми:
Теорема
1.Добуток
двох складених добутків дорівнює
складеному добутку всіх співмножників,
що входять до їх складу, взятих у тому
ж порядку, тобто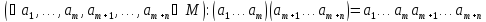 (1)
(1)
Доведення. Доведення проведемо методом математичної індукції по n.
Якщо n=1, то формула (1) прийме вигляд:
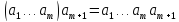 ,
яка є справедливою згідно прийнятого
означення добутку (m+1)-го
елемента.
,
яка є справедливою згідно прийнятого
означення добутку (m+1)-го
елемента.Припустимо, що формула (1) справедлива для деякого n, треба довести, що вона справедлива для n+1:
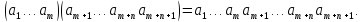
Використовуючи означення добутку (m+n)+1 елементів і асоціативність алгебраїчною операції, послідовно матимемо:
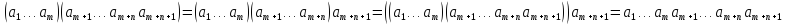
Отже, формула (1) справедлива при n, то вона справедлива і при n+1. На підставі принципу математичної індукції можна стверджувати, що формула (1) справедлива при будь-якому n.
Наслідок. В складеному добутку можна вільно розставляти дужки.
Справді, тому що у формулі (1) послідовно брати m=1, 2, …, n-1, то дістанемо:
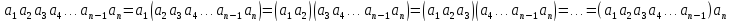
В
кожній із одержаній дужок можна на
підставі теореми 1 знову довільно
розставляти дужки, наслідок чого ми
одержимо, наприклад, таке:
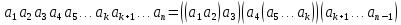
ІІІ.ОЗНАЧЕННЯГРУПИ.ПРИКЛАДИ. НАЙПРОСТІШІВЛАСТИВОСТІ ГРУП.
Означення 3. Не порожня множина G називається групою, якщо на ній означена одна алгебраїчна операція, яка задовольняє таким умовам:
Алгебраїчна операція асоціативна, тобто
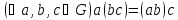 ,
,в G існує одиничний елемент е такий, що
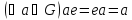 ,
,для кожного елемента
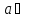 Gіснує
обернений елемент
Gіснує
обернений елемент
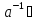 G
такий, що a
G
такий, що a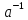 =
=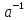 a=e.
a=e.
Якщо алгебраїчна операція, означена в групі, є додатково комутативною, то група називається комутативною або абелевою.
Приклади.
Система
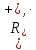 ,
де
,
де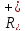 –
множина додатних дійсних чисел утворює
групу, бо (
–
множина додатних дійсних чисел утворює
групу, бо (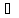 a,b
є
a,b
є
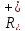 )
a,b
є
)
a,b
є
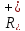 )
і операція множення задовольняє аксіомам
групи: 1) множення дійсних чисел
асоціативне. 2) в
)
і операція множення задовольняє аксіомам
групи: 1) множення дійсних чисел
асоціативне. 2) в
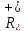 існує одиничний елемент – число1
. 3)для кожного числа а
є
існує одиничний елемент – число1
. 3)для кожного числа а
є
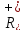 обернене число існує і належить
обернене число існує і належить
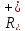 .
.Множина
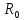 всіх дійсних чисел без нуля теж утворює
групу відносно операції множення
дійсних чисел. В цьому переконуємось
так само як і в прикладі 1.
всіх дійсних чисел без нуля теж утворює
групу відносно операції множення
дійсних чисел. В цьому переконуємось
так само як і в прикладі 1.Множина
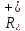 всіх дійсних чисел утворює групу
відносно операції додавання дійсних
чисел. Справді, операція “+” вR
задовольняє аксіомам групи: 1) Операція
“+” асоціативна. 2) в R
існує нейтральний елемент – число 0.
3)для всякого числа а
існує
симетричний елемент – протилежне число
–а.
всіх дійсних чисел утворює групу
відносно операції додавання дійсних
чисел. Справді, операція “+” вR
задовольняє аксіомам групи: 1) Операція
“+” асоціативна. 2) в R
існує нейтральний елемент – число 0.
3)для всякого числа а
існує
симетричний елемент – протилежне число
–а.З аналогічних міркувань система
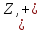 ,
деZ
– множина усіх цілих чисел є
групою.
,
деZ
– множина усіх цілих чисел є
групою.Множина
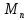 всіх невироджених матрицьn-го
порядку над полем P
утворює групу відносно операції множення
матриць. Дійсно (
всіх невироджених матрицьn-го
порядку над полем P
утворює групу відносно операції множення
матриць. Дійсно (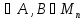 )АВ
)АВ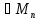 ,
бо за теоремою про визначник добутку
матриць
,
бо за теоремою про визначник добутку
матриць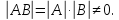 Крім того, 1)Множення
матриць асоціативне. 2)В
Крім того, 1)Множення
матриць асоціативне. 2)В
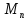 існує одиничний елемент – одинична
матрицяE.
3)Всяка неособлива матриця має обернену,
яка, крім того ж належить
існує одиничний елемент – одинична
матрицяE.
3)Всяка неособлива матриця має обернену,
яка, крім того ж належить
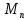 , бо на підставі теореми про визначник
добутку матриць із рівності
, бо на підставі теореми про визначник
добутку матриць із рівності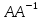 =E
виходить
=E
виходить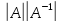 =1
і значить,
=1
і значить,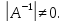
Множина
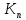 =
= всіх значень кореняn-ого
степеня
з
1 утворює групу відносно операції
множення комплексних чисел. Справді,
якщо
всіх значень кореняn-ого
степеня
з
1 утворює групу відносно операції
множення комплексних чисел. Справді,
якщо
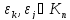 ,
бо
,
бо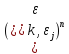 =
=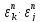 =1.
Операція множення задовольняє аксіомам
групи: 1) множення комплексних чисел
асоціативне, 2) одиниця належить
=1.
Операція множення задовольняє аксіомам
групи: 1) множення комплексних чисел
асоціативне, 2) одиниця належить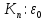 =1,
3) (
=1,
3) (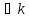 )(
)(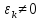 )
і
)
і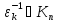 ,
бо
,
бо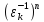 =
=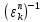 =1.
=1.Множина
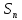 всіх підстановокn-ого
степеня очевидним чином утворює групу
відносно операції множення підстановок.
всіх підстановокn-ого
степеня очевидним чином утворює групу
відносно операції множення підстановок.
Зауважимо,
що групи в прикладах 1-4 і в 6 є абелевими,
а групи в прикладах 5 і 7 – неабелеві.
Зауважимо також, що алгебраїчні операції
в конкретних групах є або операціями
множення, або операціями додавання.
Групи, в яких алгебраїчні операції є
множенням називаються мультиплікативними,
а групи, в яких алгебраїчні операції є
додаванням , є адитивними. З наведених
прикладів видно, також, що одні групи
мають безліч елементів – нескінченної
групи (групи прикладів 1-5), інші мають
скінченну кількість елементів –
скінченні групи (групи прикладів 6 і 7).
Кількість елементів у скінченній групі
G
називається порядком цієї групи і
позначається Or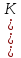 )=n,
а
в прикладі 7 Or
)=n,
а
в прикладі 7 Or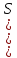 )=n!.
В
скінченних множинах групову операцію
зручно задавати за допомогою таблиць
множення, так званих таблиць Келі. В
множині
)=n!.
В
скінченних множинах групову операцію
зручно задавати за допомогою таблиць
множення, так званих таблиць Келі. В
множині
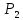 ,що
складається з двох поворотів площини
навколо нерухомої точкиО
–
точки повороту l
на кут
,що
складається з двох поворотів площини
навколо нерухомої точкиО
–
точки повороту l
на кут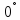 і повороту
і повороту
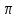 на кут
на кут
 операцією
множення задамо такою таблицею Келі:
операцією
множення задамо такою таблицею Келі:
|
|
e |
|
|
e |
e |
|
|
|
|
e |
Легко
перевірити, що множина
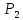 із заданою операцією є групою.
із заданою операцією є групою.
Вправи.I. Дослідити, чи утворює групу:
множина Nвсіх натуральних чисел відносно додавання і відносно множення чисел,
множина Qвсіх раціональних чисел відносно додавання і відносно множення чисел,
множина
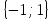 відносно операції множення чисел,
відносно операції множення чисел,множина всіх парних підстановок n-ого степеня відносно операції множення підстановок,
множина всіх непарних підстановок n-ого степеня відносно операції множення підстановок.
II.
Скласти таблицю Келі для симетричної
групи
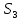 .
.
Відзначимо декілька найпростіших властивостей груп, які безпосередньо випливають з означення аксіоматики групи.
 .
В усякій групі
.
В усякій групі
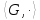 одиничний елементе
є єдиним і для всякого елемента
а
одиничний елементе
є єдиним і для всякого елемента
а Gобернений
елемент
Gобернений
елемент
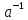 теж єдиний.
теж єдиний.
Ця властивість є безпосереднім наслідком теорем, доведених у курсі алгебри першого семестру, про єдиність нейтрального елемента і симметричного елемента в множині з асоціативною алгебраїчною операцією.
 .
Для всяких елементів а,b
.
Для всяких елементів а,b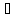 G
рівняння
ax=b
та ay=bмають
єдині розв’язки відповідноx=
G
рівняння
ax=b
та ay=bмають
єдині розв’язки відповідноx=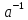 bтаy=b
bтаy=b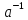 .
.
Доведення цієї властивості проводиться точно так само, як і доведення відповідної властивості полів.
 .
(
.
(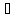 a,b
a,b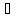 G)((
G)((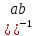 =
=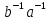 ),
тобто елемент обернений до добутку,
дорівнює добутку елементів, взятих у
зворотному порядку.
),
тобто елемент обернений до добутку,
дорівнює добутку елементів, взятих у
зворотному порядку.
Доведення.
Щоб
показати, що елемент
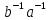 є оберненим доab
треба показати на підставі означення
оберненого елемента, що і (ab)(
є оберненим доab
треба показати на підставі означення
оберненого елемента, що і (ab)(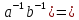 еі
еі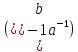 (ab)=е.
Покажемо справедливість першої рівності
(друга – аналогічно): (ab)(
(ab)=е.
Покажемо справедливість першої рівності
(друга – аналогічно): (ab)(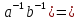 а(b
а(b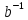 )
)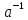 =(ae)
=(ae)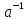 =a
=a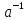 =e.
=e.
Подібно до того, як вводиться степінь з цілим показником для дійсного числа, поняття степеня з цілим показником можна ввести для будь-якого елемента групи.
Означення 4. Нехай G– група і n – ціле число. Тоді
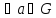 ,
,


Правила дій над степенями елементів групи ті ж, що і над степенями дійсних чисел:
4*.
Якщо G–
група, то (
 а
а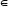 G,
G,
 m,n
m,n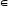 Z)
: аm
аn=аm
+ n.
Z)
: аm
аn=аm
+ n.
Доведення. В залежності від знаків чисел і розглянемо кілька випадків.
1) m ≥ 0, n ≥ 0. Тоді на підставі означення 4 і теореми 1
аm
аn
=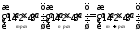 =am+n.
=am+n.
2) m ≥ 0, n ≤ 0 . Тоді n= -|n| і, використовуючи означення 4 і теорему 1, матимемо:
 =
=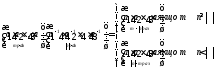
3) m ≤ 0, n ≥ 0. Розглядається аналогічно випадку 2).
4 ) m ≤ 0, n ≤ 0. Розглядається аналогічно випадку 1).
Наслідок.
В групі G( а
а G
) (
G
) ( n
n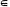 Z)
: (аn)
-1
= а-n
, тобто , елементом, оберненим до аn,є
а-n
Z)
: (аn)
-1
= а-n
, тобто , елементом, оберненим до аn,є
а-n
Справді, аnа-n = аn - n= а0 = е,
а-n аn = а – n + n=а0= е.
Методом
математичної індукції властивість 4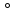 можна розповсюдити на довільну скінчену
кількість співмножників
можна розповсюдити на довільну скінчену
кількість співмножників
5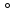 .
В групіGдля
.
В групіGдля
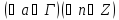 :(
:( )n=
)n=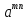
Доведення. Розглянемо два випадки.
m – довільне, n
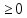 .
Тоді на підставі властивості 4
.
Тоді на підставі властивості 4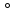 і означення 4
і означення 4
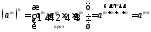
m – довільне,n<0. Використовуючи означення 4, наслідок з властивості 4
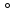 і перший пункт доведення даної
властивості, матимемо:
і перший пункт доведення даної
властивості, матимемо:
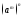 =
=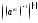 =
=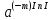 =
=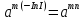 .
.
Вправа. Перефразувати властивості 3-5 для адитивних груп.
Зауважимо,
що при переході до адитивних груп
поняття n-ого
степеня елемента
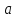 замінюється поняттямn-кратного
елемента
замінюється поняттямn-кратного
елемента
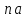 елементу
елементу