Показникова форма комплексного числа

Вище розглядалася тригонометрична форма запису комплексного числа: z=r(cosφ+isinφ).

Формула Ейлера дозволяє, очевидно, комплексне число z (z≠0) записати більш компактно: z=re^iφ, де φ – якийсь аргумент числа z, а r – його модуль. Це так звана показникова чи експонентна форма запису комплексного числа.

Для отримання показникової форми комплексного числа немає необхідності попередньо записувати його в тригонометричній формі.

Приклад 1. Запишемо в показниковій формі число і.

Розв’язання. Зобразимо число і на комплексній площині у вигляді вектора. Його довжина дорівнює 1, а кут нахилу до дійсної осі дорівнює . Отже, |i| =1,arg i=, і=1·. Це й буде показниковою формою числа і.

Приклад 2. Запишемо число z =1-i в показниковій формі.

Розв’язання. Число z = 1-і має модуль і аргумент, тому його показникова форма така: 1-і =.

Між іншим, маючи показникову форму комплексного числа z, ми можемо вказати його модуль і аргумент. Наприклад, якщо z =5, то |z|=5. Один із аргументів числа z дорівнює , так що z=5і.

Розглянемо правила дій з аргументами і модулями добутків і часток комплексних чисел, відмінних від нуля.

Нехай z=z₁·z₂. Запишемо кожен множник в показниковій формі: Тоді,Звідси видно, щоz має своїм модулем число r₁·r₂, а одним із аргументів – число φ₁+φ₂.

Отже, при множенні двох комплексних чисел їх модулі перемножуються, а аргументи додаються.

У випадку рівних множників ми отримуємо наступне правило: при піднесенні комплексного числа z до степеня з натуральним показником його модуль підноситься до степеня з тим же показником, а аргумент множиться на показник степеня.

Таким чином, якщо число z має модулем число r, а одним із своїх аргументів число φ, то число zⁿ має модуль rⁿ, а одним із своїх аргументів число nφ.

Також, при будь-яких натуральних m i n правильна рівність:

|z^m·n|=|z|^m·n =|z^m|ⁿ.

Приклад. Спростити вираз w =.

Розв’язання. Позначимо z = , тоді: |z| = 2,arg z = . Тому, |w| = |z|⁶ = 2⁶=64, а один із аргументів числа w дорівнює , тоді w = 64e^-iπ = -64.

Нехай тепер z=z₁/z₂. Запишемо ділене і дільник в експоненціальній формі: Тоді, =. Видно, щоz₁/z₂ має модулем число , а одним із своїх аргументів – число φ₁-φ₂. Отже, при діленні комплексних чисел їх модулі діляться, а аргументи віднімаються.

Приклад. Нехай z = , де а і b – два комплексних числа, причому |a|=|b|. Чи вірно, що z – чисто уявне число?

Розв’язання. Позначимо модулі чисел а і b буквою r, а їх аргументи відповідно α і β. Запишемо дані числа в показниковій формі: а = re^iα, b = re^iβ. Тоді: ==.

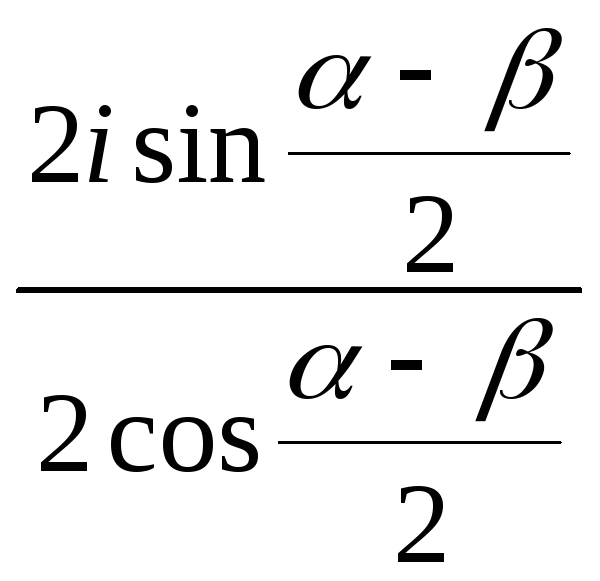Бачимо, що z – чисто уявне число.

Чи можна порівняти комплексні числа? Іншими словами, чи можливо упорядкувати комплексні числа так, щоб сформулювати правило, яке б дозволяло для будь-яких двох із них сказати, яке з них є меншим, а яке більшим? Виявляється, що таке правило встановити можна, і навіть не одним способом. Найпростіший із способів – лексикографічний, аналогічний до того, який використовують при упорядкуванні слів у словнику. Візьмемо два числа z₁=a₁+b₁i i z₂=a₂+b₂i. Будемо вважати, що z₁<z₂ (або, що число z₁ попереднє для числа z₂), якщо виконується одне з двох:

1. а₁<а₂ (незалежно від того, що більше: число b₁ чи b₂);

2. а₁=а₂, але b₁<b_2.

Наприклад, 5+4і<6+3і.

Розглянемо інший спосіб впорядкування комплексних чисел. Нехай z₁ і z₂ – два комплексних числа, (φ₁=argz₁, φ₂=argz₂, r₁= |z₁|, r₂ = |z₂|). Домовимося вважати, що z₁< z₂, якщо виконується одна з умов:

1. r₁< r₂ (незалежно від того, що більше: φ₁ чи φ₂);

2. r₁=r₂, але φ₁<φ₂.

При застосуванні кожного із цих способів визначене для комплексних чисел поняття «менше» має «властивість транзитивності»: якщо z₁<z₂ і z₂<z₃, то z₁<z₃. Але для таких означень не зберігається важлива властивість, що часто використовується при розв’язуванні нерівностей для дійсних чисел: якщо а<b і с>0, то ас<bc. Наприклад, нехай а=-і, b=і, с=і. Тоді, за попередньою властивістю ми мали б вважати, що с>0, а а<b. Але а·с=-і·і=1, b·с=і·і=-1, і нерівність ас<bc вже невірна. Такі відхилення від привичних властивостей нерівностей змусили відмовитися у випадку комплексних чисел від розгляду понять «більше» і «менше».