
- •Введение
- •1 Основные характеристики импульсов
- •2 Спектры импульсов
- •2.1 Общие положения
- •2.2 Спектр периодической последовательности импульсов
- •2.3 Спектр периодической последовательности прямоугольных импульсов
- •2.4 Спектр одиночного импульса
- •2.4.1 Расчет спектра одиночного прямоугольного импульса
- •2.4.2 Расчет спектра экспоненциального импульса
- •2.4.3 Расчет спектра колокольного импульса
- •3 Задания для самостоятельной работы студентов
2 Спектры импульсов
2.1 Общие положения
При временном представлении сам импульс (сигнал) представляется в виде функции времени. Часто необходимо сконцентрировать внимание не на изменениях сложного сигнала во времени, а на том, из каких простых гармонических колебаний он состоит. В этих случаях прибегают к спектральному представлению сигнала, в основе которого лежат преобразования Фурье. При спектральном представлении сигнал представляется не функцией времени, а функцией частоты. Совокупность гармонических колебаний, на которые может быть разложен данный сигнал, называют спектром сигнала. Полоса частот, в которой наблюдаются гармонические колебания, составляющие данный сигнал, называют шириной его спектра.
Заданное колебание
![]() можно представить в виде комбинации
простых составляющих или путем подбора
нескольких функций
можно представить в виде комбинации
простых составляющих или путем подбора
нескольких функций![]() и коэффициентов
и коэффициентов![]() так, чтобы
так, чтобы
![]() .
(1)
.
(1)
Ряд сходится, если функция
![]() удовлетворяет
условиям Дирихле. Наиболее точное
приближение будет при
удовлетворяет
условиям Дирихле. Наиболее точное
приближение будет при
![]() .
(2)
.
(2)
При этом ряд называется обобщенным рядом Фурье,
где
![]() -
совокупность ортогональных функций.
-
совокупность ортогональных функций.
Для ортогональных функций выполняется условие

![]() ;
;![]()
![]() .
.
Если при этом
 ,
то систему называют ортонормированной
(ортонормальной).
,
то систему называют ортонормированной
(ортонормальной).
Примеры ортогональных колебаний
![]() и
и![]() .
.
Для разложения сигналов можно использовать элементарные функции, а также ряд специальных систем функций, обладающих свойством ортогональности на различных отрезках (тригонометрические функции кратных аргументов, полиномы Эрмита, Лежандра, Чебышева, функции Бесселя, Лагерра и ряд других).
Обычно для теоретического анализа
целесообразно выбирать систему функций,
требующую наименьшего числа членов
ряда для заданной точности представления
колебания. Однако в ряде случаев решающим
при выборе
![]() является простота физического
осуществления (генерирования) этих
функций.
является простота физического
осуществления (генерирования) этих
функций.
Таким свойством обладает, в частности, система тригонометрических функций кратных аргументов. Причем их форма не изменяется при прохождении через линейные цепи, а также имеется возможность использовать символический метод, разработанный для анализа передачи гармонических колебаний через линейные цепи.
2.2 Спектр периодической последовательности импульсов
Если взять в качестве функций
![]() тригонометрические функции
тригонометрические функции
![]()
![]()
![]()
![]()
![]() ;...
;...
![]() где
где![]() -интервал
ортогональности функции, он совпадает
с периодом колебания;
-интервал
ортогональности функции, он совпадает
с периодом колебания;
![]() .
.
Ряд Фурье принимает следующий вид:
![]() ,
(3)
,
(3)
где
 ;
(4)
;
(4)
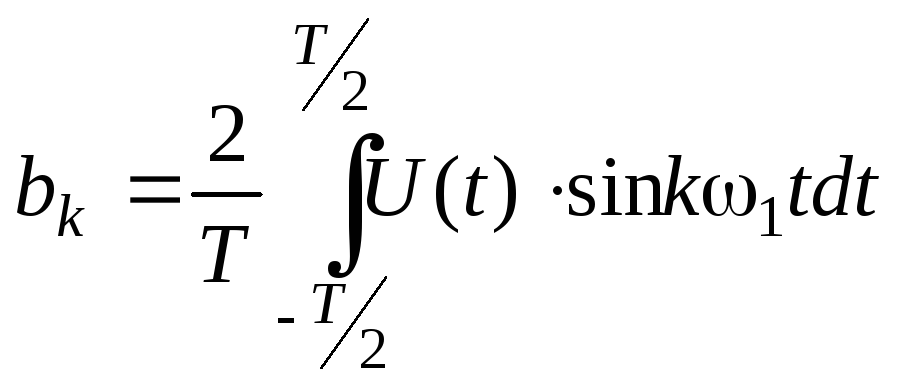 ;
(5)
;
(5)
 (6)
(6)
или
![]() ,
(7)
,
(7)
где
![]() ;
;![]() .
.
Ряды Фурье могут быть записаны и в комплексном виде
![]()
![]() .
.
Учитывая, что
![]() ,
,
получим
![]() .
(8)
.
(8)
 .
(9)
.
(9)
Формулы называются парой преобразований
Фурье. Вторая формула из них позволяет
найти спектр, т.е. совокупность
гармонических составляющих, образующих
в сумме колебание
![]() .
.
Спектр периодической последовательности
импульсов состоит из постоянной
составляющей и множества гармонических
составляющих, частоты которых образуют
дискретный ряд значений
![]() (
(![]() )
кратных основной частоте колебаний
)
кратных основной частоте колебаний![]() .
Амплитуды гармонических составляющих
или сокращенно гармоник равны
.
Амплитуды гармонических составляющих
или сокращенно гармоник равны![]() ,
а начальные фазы
,
а начальные фазы![]() .
Такой спектр называется дискретным или
линейчатым.
.
Такой спектр называется дискретным или
линейчатым.
Постоянную составляющую можно
рассматривать как гармонику с нулевой
частотой колебания и амплитудой
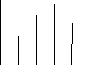
![]() . На рисунке 2 показана амплитудная
спектральная диаграмма периодического
сигнала, а на рисунке 3 - фазовая
спектральная диаграмма периодического
сигнала.
. На рисунке 2 показана амплитудная
спектральная диаграмма периодического
сигнала, а на рисунке 3 - фазовая
спектральная диаграмма периодического
сигнала.




![]()
![]()



0
![]() 0
0![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рисунок 2 Рисунок 3
В разложении
суммирование членов происходит как по
положительным так и по отрицательным
![]() .
Это означает, что комплексный ряд Фурье
содержит гармоники не только с
положительными, но и с отрицательными
частотами. Совершенно ясно, что последние
никакого физического смысла не имеют.
Они появляются только как следствие
формального представления тригонометрических
функций в виде совокупности показательных
функций с мнимым аргументом.
.
Это означает, что комплексный ряд Фурье
содержит гармоники не только с
положительными, но и с отрицательными
частотами. Совершенно ясно, что последние
никакого физического смысла не имеют.
Они появляются только как следствие
формального представления тригонометрических
функций в виде совокупности показательных
функций с мнимым аргументом.
